一类随机四阶抛物型方程的解的稳定性研究
(南京邮电大学通达学院,江苏 扬州 225127)
近年来,随机微分方程(SDEs)和随机偏微分方程(SPDEs)因其在自然科学、工程控制、生物等领域的广泛应用而受到越来越多的重视和研究.人们主要关心方程解的存在唯一性及稳定性.目前已有一些好的研究方法,如Lyapunov函数方法、逐次逼近法、大偏差理论、不动点原理等.其中,不动点原理因其在解的稳定性研究方面简单有效而受到广泛使用,尤其是那些带Markov链和Possion跳的问题.但是,目前已出版的文献大多是讨论随机微分方程或者随机热方程(二阶抛物),而很少有随机四阶抛物型偏微分方程的解的稳定性结果.如文献[1]讨论了线性随机四阶抛物型方程的解的稳定性.
到目前为止,尚没有非线性随机四阶抛物型方程的解的稳定性结果.
本文考虑一类带Markov链的非线性随机四阶抛物型方程的解的稳定性问题.利用不动点原理,我们不但得到了解的存在唯一性,还得到了温和解的p阶矩指数稳定性.
一、记号、模型及定义
常用记号:本文用到的记号简介如下:
(N5)拉普拉斯算子:,散度:
模型:本文主要考虑如下非线性随机四阶抛物型偏微分方程:
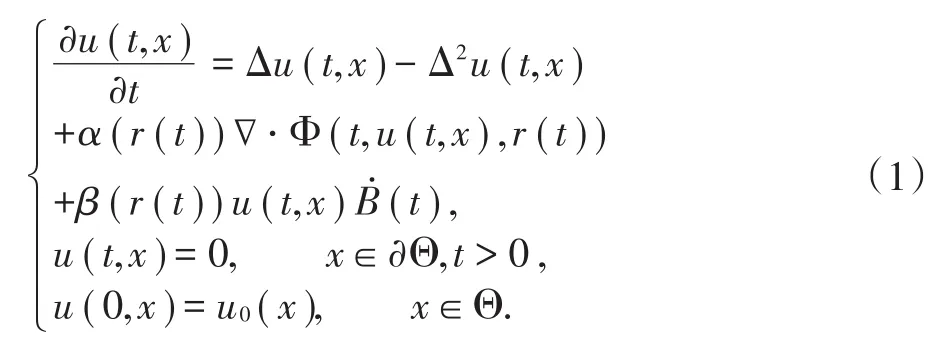
其中α,β:S→R,记αi=α(i),βi=β(i),Φ:[0,T]×L2(Θ)×S→L2(Θ)为Ft可测的,初值u0为F0可测随机变量,与r(⋅)和B(⋅)相互独立,且∀p> 0,Ε‖u0‖p<∞.
定义1:取值于L2(Θ)的随机过程u:={u(t,⋅)}t∈[0,T]称为方程(1)的温和解,若其满足:
(i)u∈C([ 0 ,T] ;L2(Θ)),∀t∈ [ 0 ,T],且u(t)是Ft适应的,满足:
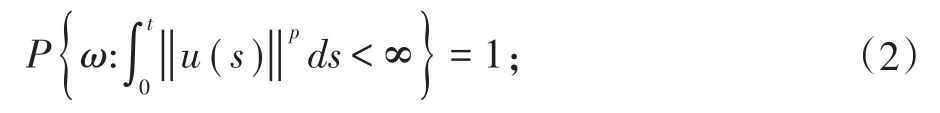
(ii)u满足随机微分方程
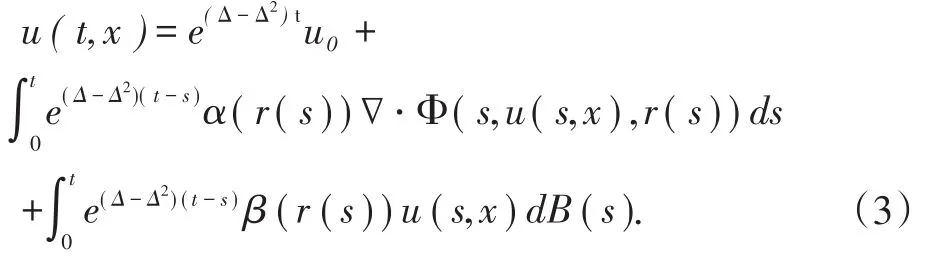
定义2:方程(1)称为是p阶矩指数稳定性的,若存在常数δ>0,C>0使得
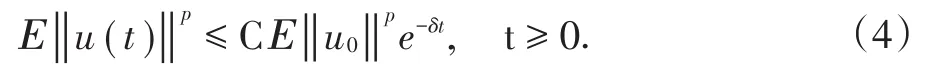
最后,我们给出定理证明的一些必要假设.
假设:(A1)‖etΔ‖ ≤ Me-γ t,M为常数,γ> 0;
(A2)Φ 是满足以下条件的算子:∀u,v∈L2(Θ),p≥ 2,存在正常数LΦi(i∈S)使得:Φ(t,0,i)=0,‖Φ(t,u(t,x),i)-Φ(t,v(t,x),i)‖ ≤LΦi‖u(t,x)-v(t,x)‖;
(A3) sup1≤i≤N|αi|LΦi<∞,sup1≤i≤N|βi|<∞.
二、主要定理
本节我们将用不动点原理讨论方程(1)的温和解的存在唯一性及p阶矩指数稳定性.
引理1[4]:设G(t,x)是ut=Δu-Δ2u的基本解,则
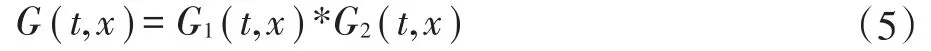
其中,G1(t,x)为ut-Δu=0 的基本解,满足;G2(t,x)为ut+Δ2u=0 的基本解,满足;“*”指卷积,“”指v的 Fourier变换.记eΔt:=G1(t,x),e-Δ2t:=G2(t,x),e(Δ-Δ2)t:=G(t,x).
引理2[3]:设G1(t,x),G2(t,x),G(t,x)如上,则:
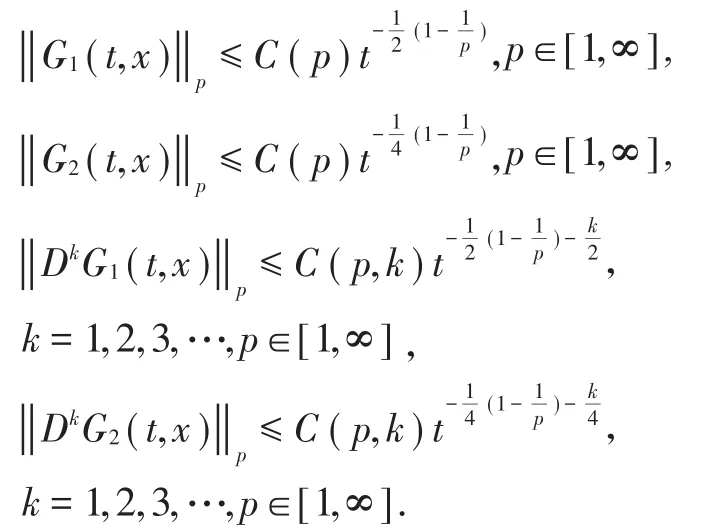
引理3:若etΔ满足假设(A1) , 则
证明:由卷积的Young不等式,引理1及引理2得:
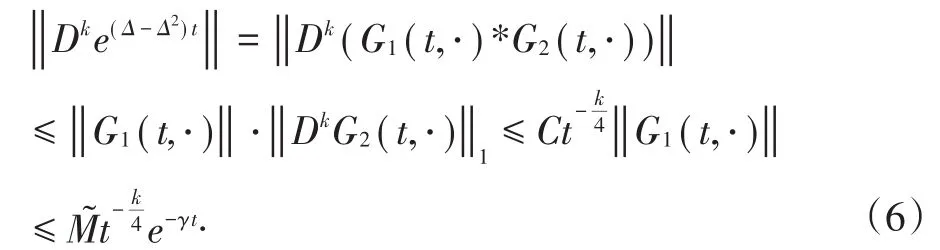
其中>0为常数,如不特别说明,我们将不再加以区分.
特别地,若k=0,则
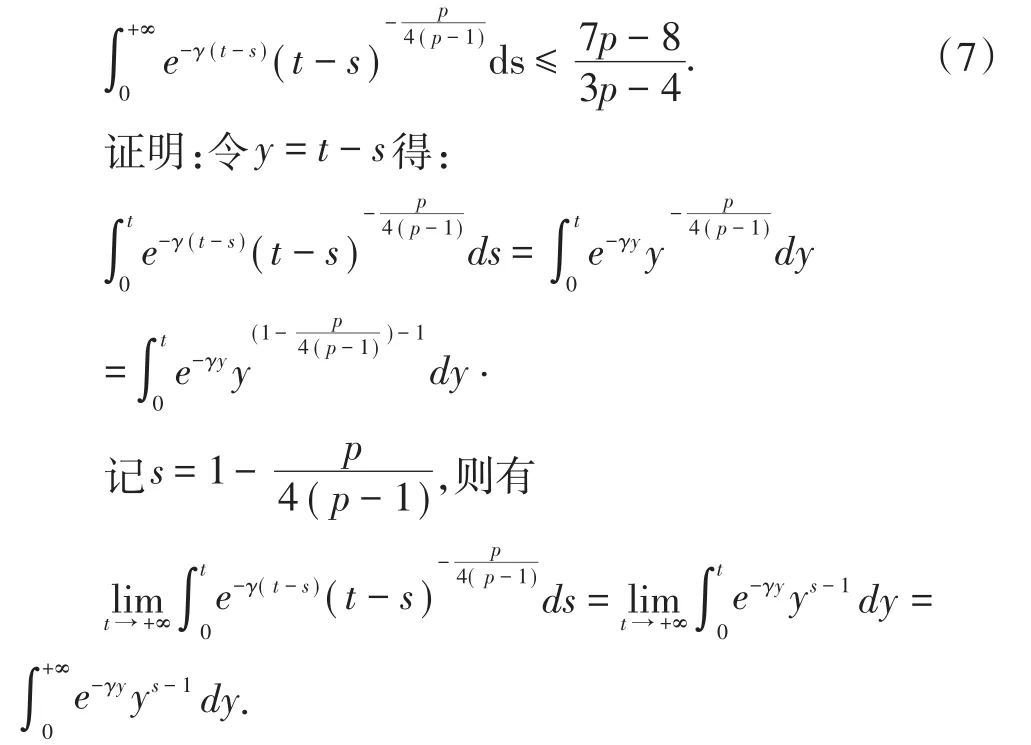
当p≥2时有s>0.故由Γ-函数的特点知此时积分收敛.又
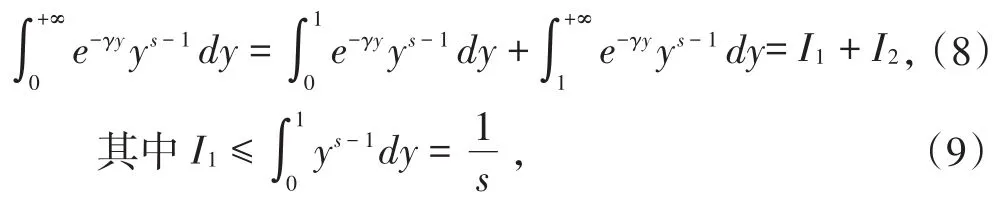

证明:设H是所有Ft适应的连续过程的Banach空间,u(t,x)∈H,满足Ε‖u(t,x)‖p≤M*Ε‖u0‖pe-ηt,t≥ 0,M*>0,0<η<γ.H中的范数定义为
我们定义算子φ :H→H:

由Cp不等式[2]得:
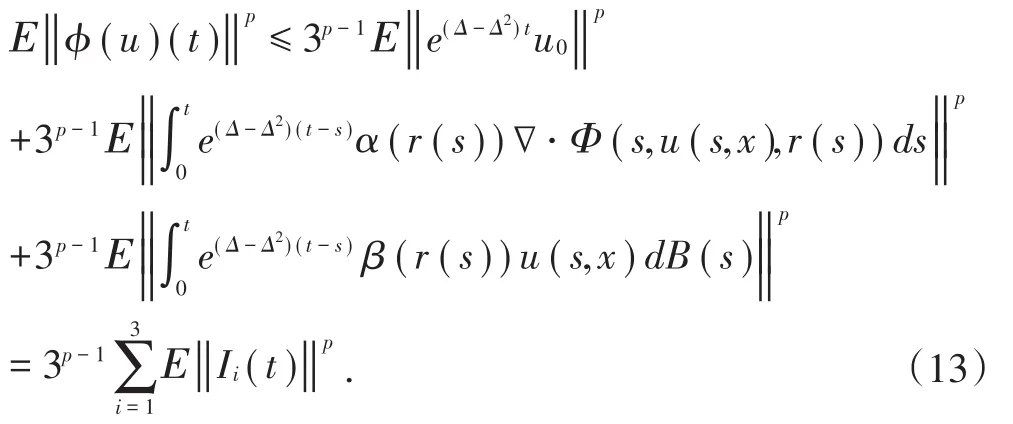
显然φ在[0,+∞)上是p阶矩连续的.以下我们分两步证明.
步骤1:φ(H)⊆H.由引理3得:

由假设(A1-A3),引理3,引理4及Hölder不等式得:
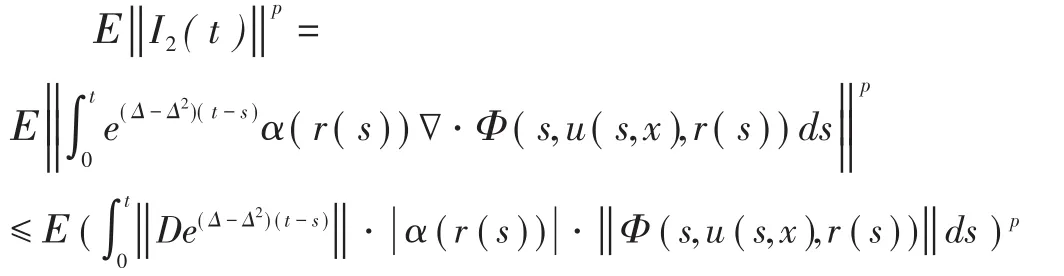
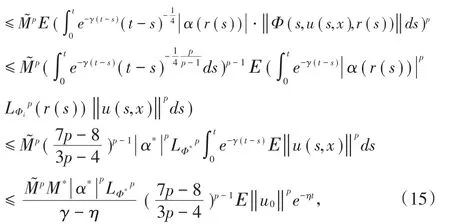
由引理3和BDG不等式[5]得:
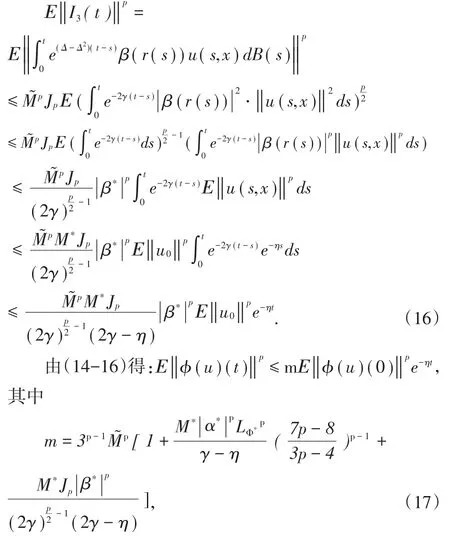
由此φ(H)⊆H得证.
步骤2:φ是压缩映射.∀u,v∈H,u(0,x)=u0(x)=v(0,x),考虑下式:
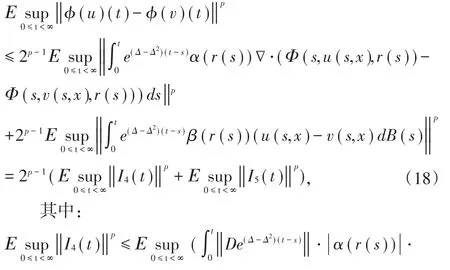

由条件(11)∈(0,1)得:φ是压缩映射.
由不动点定理可知φ在H中有唯一不动点u(t,x),且由以上证明可知u(t,x)是p阶矩指数稳定的.由此定理1证毕.

