最小风险贝叶斯决策融合的多点触摸身份认证*

孙子文，李 富，庞永春

(江南大学物联网工程学院，江苏 无锡 214122)

1 引言

随着移动智能生活时代的到来，智能手机的重要性日益提升，如何确保手机中的重要数据只能由合法用户访问成为亟需解决的问题。当前，智能手机对于用户身份的合法性判别一般采用传统的密码或图案，安全度不高，容易遭受暴力破解。基于生物特征身份认证方法的出现，为模式识别领域中研究合理有效的身份识别认证提供了多种选择。

当前，用户解决身份认证问题的方法基本上可以分成两大类：依据生物生理特征进行身份识别认证和依据生物行为特征进行身份识别认证。依据生理特征进行身份识别认证的方法主要有基于手掌进行认证[1]、基于虹膜进行认证[2]和基于指纹进行认证[3]等。依据生理特征进行身份认证的方法在识别率上达到了很高的水准，但是其数据采集的难度及其计算的复杂度问题限制了其在智能手机上的应用。依据生物行为特征进行身份认证的方法主要有基于步态进行认证[4,5]、基于动态手势进行认证[6]和基于击键进行认证[7]等。采用生物自身独有的、不易模仿的特征进行身份识别认证，使身份认证具有较好的安全性和便捷性。

多点触摸身份认证作为生物行为特征方法的一种，是通过智能终端中内置的传感器采集多指的手势数据，并结合相应的算法完成用户身份合法性的判定。当前智能手机屏幕的扩大趋势，使得多点触摸功能在智能手机中的应用得以实现。通过多点触摸获取特征数据进行身份识别认证的常见方法包括：基于多层感知器MLP(MultiLayer Perceptron)的身份识别认证，通过智能终端获取特征数据，完成用户身份的识别认证[8]；基于支持向量机分布估计SVDE(Support Vector Distribution Estimation)算法的身份识别认证，通过智能终端获取手势轨迹及签名的特征数据完成用户身份合法性的判定[9]；基于改进豪斯多夫距离MHD(Modified Hausdorff Distance)算法的身份认证，即通过匹配计算认证特征与模板特征获得相应的匹配值，并结合组合规则获得匹配认证的结果[10]；基于局部特征进行动态时间规整DTW(Dynamic Time Warping)距离计算的身份认证，即对全局特征进行马氏距离计算，然后根据距离值，以随机森林分类器(Random Forest Classifier)作为决策级融合容器，根据融合后的结果判定用户的真实性[11]；基于模糊推理系统FIS(Fuzzy Inference System)的身份认证，通过结合个人识别码PIN(Personal Identification Number)数字、食指压力等构成双重认证系统，实现用户的认证过程[12]；基于动态时间规整DTW的身份认证，通过点触摸行为中两两手势序列之间的距离，采用模板匹配方法完成用户身份是否合法的判定[13]。但是，文献[8-13]中的身份识别方法存在以下不足：对于身份认证过程中将真实用户判断为入侵用户的风险和将入侵用户判断为真实用户的风险等同。而在实际中，将入侵用户判断为真实用户的风险明显大于将真实用户判定为入侵用户的风险。

针对文献[8-13]中方法存在的问题，本文采用基于最小风险贝叶斯决策融合的多点触摸身份认证方法。在用户进行身份认证过程中，首先采用逻辑回归-均值动态时间规整LR-MDTW(Logic Regress - Mean Dynamic Time Wrapping)算法对多点触摸手势信息进行局部决策分类；然后以贝叶斯规则为基础，引入损失函数，获取局部决策结果，采用最小风险贝叶斯融合局部决策结果，获得最小平均风险，降低认证的漏警率和虚警率。

2 最小风险贝叶斯分布式决策融合分类

基于最小风险贝叶斯决策融合分类方法的整体流程如图1所示，图中R(ωtrue)、R(ωfalse)分别表示决策为真实用户的风险和决策为入侵用户的风险。本文中分布式融合决策分类分为3步：首先进行局部决策，即将多点触摸手势轨迹所提取的特征向量信息分别经过LR-MDTW分类器进行局部分类，获得各指序列的局部决策后验概率；然后计算各指序列的局部决策条件风险；最后计算平均最小风险的分类结果并将此结果作为最终全局分类结果。

2.1 数据采集与特征提取

(1)

(2)

为了能够较为全面地体现真实用户与入侵用户的行为误差，本文分别选用用户归一化后X轴坐标值的一阶和二阶导数、归一化后Y轴坐标值的方向一阶和二阶导数、手势运动轨迹方向、手势运动轨迹曲率；轨迹点对应的压力值和指间距离作为特征信息[14]。其中指间距离li,j表示为式(3),触摸曲线的曲率表述为式(4)，指尖压力表述为式(5)：

(3)

(4)

(5)

2.2 分布式决策融合

2.2.1 LR-MDTW局部分类

一般常见的DTW算法是在测试数据与模板数据之间建立合理的匹配路径，用于消除两种数据之间存在不匹配的情况，为获取动态匹配的相似性及分类问题提供了解决途径[16]。但是，常见的DTW算法反映的是两种数据之间存在的整体差异，不会影响数据序列两两对齐点间的差异性。然而在实际应用的过程中，忽略对齐点差异及特征权重的假设会使认证结果存在较大误差。文献[17]表明，在计算测试数据与模型数据的匹配程度时，如果考虑数据对齐点的差异性以及特征数据权重分配的情况，可以更好地体现数据的差异性。LR-MDTW算法是对常用DTW算法的改进，具体描述如下：

定义数学描述G(N)=(g1,g2,…,gn,…,gN)为测试模板数据序列，R(M)=(r1,r2,…,rm,…,rM)为参考模板数据序列，其中，N和M分别表示测试模板数据序列和参考模板数据序列的个数；采用最小累计距离对匹配路径进行量化处理，其数学表达式如式(6)所示：

1≤n≤N,1≤m≤M

(6)

其中,gn、rm分别表示测试模板数据序列和参考模板数据序列；n、m分别表示测试模板数据序列和参考模板数据序列中的点序号；d(gn,rm)为gn与rm之间的距离，则由式(7)和式(8)可以得出最小累计平均距离D(gN,rM)：

Dir(gn,rm)=d(gn,rm)+min(Dir(gn-1,rm),

Dir(gn-1,rm-1),Dir(gn-1,rm-2))

(7)

D(gN,rM)=Dir(gN,rM)/number

(8)

Dj=[D0,Dj,1,Dj,2,…,Dj,8]T

(9)

特征权值向量可表述如式(10)所示：

w=[w0,w1,w2,…,w8]T

(10)

样本特征向量与权值向量的线性组合如式(11)所示：

wTDj=w0+w1Dj,1+w2Dj,2+…+w7Dj,8

(11)

为了能够更好地区分真实用户与入侵用户，采用逻辑回归[18]方法构建代价函数训练用户的各特征信息权重值，其代价函数如式(12)所示：

(12)

整体代价函数如式(13)所示：

(1-Lj)log(1-H(wTDj))

(13)

其中,n=α+λ-1。本文需要得到J(w)最小值，用于获取最佳的特征向量w，且在解决J(w)的最优解问题上采用梯度下降法[19]，不同特征对应的权重值wk的更新迭代规则如式(14)所示：

(14)

其中,β为梯度下降中的前进步长，Dj,k为训练集中的第j个数据的第k个特征的MDTW距离。当J(w)停止负方向下降时，此时取得权重向量w的最优值[16]。

2.2.2 最小风险贝叶斯决策模型

在用户身份认证过程中，总是希望减小错误分类的风险。根据这样的要求，利用概率论中的贝叶斯理论，得出使所有风险最小的分类规则，称其为最小风险贝叶斯决策[20]。

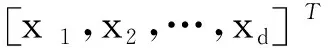
(15)

其中,P(x|ωj)和P(ωj)分别表示已知的先验概率和条件概率。对于指定的x，采用决策αi的条件风险R(αi|x)可以表示为采用αi所造成的平均损失，如式(16)所示：

(16)

决策函数α(x)的期望风险R可表示为式(17)：

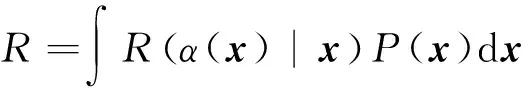
(17)

2.2.3 最小风险贝叶斯决策的融合身份认证

用户身份认证过程中存在虚警和漏警两种错误分类的可能性。其中虚警表示将真实的用户判断为入侵用户的情况，漏警表示将入侵用户判断为真实用户的情况。对于用户而言，两种错误造成的风险是完全不同的，一般来说漏警对用户所带来的风险更大。因此，为了降低漏警率，本文引入最小风险贝叶斯决策融合规则。

设定在用户身份认证过程中，状态空间和决策空间是相同的，都是二维空间，即：

状态空间Ω={ω1,ω2}={ωtrue,ωfalse}

决策空间A={α1,α2}={ωtrue,ωfalse}

其中，ωtrue,ωfalse分别表示真实用户和入侵用户。在证据集为Z={z1,z2,…,zl}的情况下，决策的风险R如式(18)所示：

Ri(αi|xj),j=1,2,…,n;

i=1,2;α1=ωtrue,α2=ωfalse

(18)

此时的损失函数：λi,j=λ(αi,ωj)，且

λ1,1=λ(ωtrue,ωtrue)=λ2,2=λ(ωfalse,ωfalse)=0

(19)

λ1,2=λ(ωtrue,ωflase)<λ2,1=λ(ωfalse,ωtrue)

(20)

其中，式(19)表示决策分类的结果正确，即将真实用户判定为真实，将入侵用户判断为入侵，因此此时的决策是没有损失的；式(20)表示在决策中，将真实用户分类为入侵用户的风险要小于将入侵用户分类为真实用户的风险。对于证据集中不同的证据来说，决策的条件风险R取值为：

λ1,2P(ωfalse|zl)

(21)

λ2,1P(ωtrue|zl)

(22)

所得最终的融合结果：

(23)

3 实验结果及性能分析

3.1 实验设置

3.1.1 实验环境及数据获取

实验仿真平台选用Matlab 7.11.0，在Windows系统环境下进行仿真实验。实验数据库中数据均通过三星SVM-G9008V智能手机采集获取，并且数据来源于8位真实用户和10位入侵用户，其中每位真实用户需要按照要求完成相应的指定动作，每个手势动作采集800组，同时各个参与的入侵用户需要依次观看各个真实用户的手势，然后根据观察采集模仿每位合法用户的手势动作200组。最后可得包括8×800=6400组真实用户手势数据及10×8×200=16000组入侵用户手势数据的数据库。

3.1.2 参数设置

多点触摸身份认证过程中使用两个参数指标进行身份认证系统的性能评估，分别为：错误拒绝率FRR(False Rejection Rate)，即参与测试的真实用户被认定为入侵用户的概率；错误接受率FAR(False Acceptance Rate)，即入侵用户被判定为真实用户的概率。在分布式决策融合的第一阶段，规定LR-MDTW局部分类中的阈值选取规则如下：轮流选择每位真实用户的200组手势数据作为合法数据，选择每位入侵用户的80组模仿手势数据作为非法数据，计算获得不同阈值条件下对应的FAR和FRR。由于在相同阈值时，食指和中指所对应的FAR和FRR并不相同，本文会根据各个手指在不同阈值下所对应的FAR和FRR，获取不同阈值所对应的FAR和FRR的均值，然后计算FAR和FRR的均值获得最终的判断阈值。

3.2 实验结果分析

表1所示为采用LR-MDTW算法对多点触摸进行身份认证且未对多指数据进行融合前的认证性能。在认证过程中，以用户信息的安全性为第一考虑要素，即要求在认证过程中以降低漏警率为首要目标。

Table 1 Authentication performance without fusion rules表1 未采用融合规则的认证性能

将各指所提取的特征信息分别经过LR-MDTW算法进行局部预分类，并根据平均最小风险贝叶斯融合规则将用户多点触摸手势信息进行决策分类。在本文的最小风险贝叶斯决策融合分类中，以降低认证漏警率为首要指标，在保证漏警率低于1%的情况下尽可能降低虚警发生的概率，在本实验过程中取损失函数λ1,2=1.4,λ2,1=1.6，实验结果如表2所示。

Table 2 Comparison of simulation results and performance表2 仿真结果及性能对比

由表2中数据可知，在多点触摸身份认证过程中，采用“与”融合所得到的FAR和FRR的最大值分别为0.96%和7.66%，均值分别为0.42%和6.30%；采用“或”融合所得到的FAR和FRR的最大值分别为1.88%和5.76%，均值分别为1.19%和5.09%；采用本文所提出的最小风险贝叶斯决策融合所得到的FAR和FRR的最大值分别为1.02%和2.43%，均值分别为0.48%和2.07%。

上述三种融合方法中，“与”融合决策具有最低的错误接受率，即采用“与”融合时，认证过程的漏警率最低，但同时却拥有最高错误拒绝率，提高了认证过程的虚警率，此时的认证安全风险较大；“或”融合决策方法虽然降低了错误拒绝率，但是却大大提高了错误接受率，即提升了漏警率，因此这种认证方式也不可行；本文采用的基于最小风险贝叶斯决策的融合方法不仅有效消弱了决策风险,降低了虚警率，而且获得了相对较低的漏警率，最终在认证过程中获得了较为理想的分类准确率。

4 结束语

为了提高智能手机中多点触摸身份认证的综合认证效果，降低在认证过程中的漏警率和虚警率，本文提出了一种基于最小风险贝叶斯决策融合的多点触摸身份认证方法。首先对各指手势序列进行LR-MDTW局部决策分类，继而通过计算局部条件风险来获得最小平均风险的最终决策分类结果。仿真结果表明，采取最小风险贝叶斯决策融合所获得的分类结果相比于采用“与”融合和“或”融合具有最小的分类风险，效果更好。