基于灰色马尔科夫模型的家纺流行色趋势预测

史爱武，胡志强，叶 威，陈 鄂

(武汉纺织大学 云计算与大数据研究中心，武汉 430200)

家纺流行趋势是指通过对家纺历史数据进行定性以及定量的分析，预估家纺的面料、花色以及图案在未来一段时间内的大众偏爱走向.在家纺产品的设计研发过程中，色彩是一种很重要的设计元素，它将直接体现出其所有者的个性和时尚需求，同时也会在很大程度上影响着市场消费需求[1],它是一个时期、一定社会的政治、经济、人文环境以及人们心理活动等因素的综合产物.对社会群体而言，流行趋势的立意与传播是以社会的心理变化为依据的，是可以认识预测的[2].流行色的演变大约为5～7年，其中，黄金销售期一般为1～2年，因此流行色是具有时间和空间定义的特定色彩[3].

目前对于家纺流行色预测有一定的研究[4]，吴湘济[5]基于家纺产品流行现状，分析了家纺产品的流行色，指出了近年来家纺流行色的主导色彩；刘欢等[6]使用WGSN、Pantone View、Trend Book等国际八大流行预测机构发布的2013年春夏色彩趋势报告作为数据源，使用NCS色彩的色彩三角和色彩圆环分析工具，对获取的色彩数据进行量化统计分析；Lin等[7]应用灰色系统理论与灰色神经网络方法，以1995-1999年日本秋冬男装流行色数据为研究对象，对服装流行色色相以及色调进行了预测.这些研究普遍存在两个问题：一是偏向定性分析而缺少定量分析；二是趋势分析方法存在不足，数据挖掘深度不够.其中，灰色预测模型以其较小的样本量，较高的预测精度被应用于流行色预测中，然而，当数据离散程度越大，即数据灰度越大时，预测精度越差，并且GM(1,1)不太适合中长期的预测[8].本文结合灰色模型与马尔科夫模型对家纺流行色进行趋势预测，即用灰色模型解释流行色发展趋势，应用马尔科夫链对灰色预测的残差进行调整，以提高预测的精度.

1 灰色马尔科夫预测模型

1.1 灰色系统理论

灰色系统是信息不完全的系统.所谓“信息不完全”通常是指：系统结构不完全清楚；系统因素不完全明确；因素关系不完全清楚；系统的作用原理不完全明了.严格来讲，灰色系统是绝对的，而黑色与白色系统是相对的.灰色系统理论与统计分析方法的区别在于：前者致力于现实规律的探讨，后者致力于历史规律的研究.灰色系统与模糊数学的区别在于对系统内涵和外延处理态度的不同，研究对象内涵与外延性质的不同.灰色系统着重外延明确，内涵不明确的对象.对于家纺流行色系统，影响其变化的因素很多，有已知的，也有不明确的.因此，家纺流行色系统是灰色系统[9]，从预测的不确定性方面来讲，采用灰色系统对家纺流行色进行趋势预测是恰到好处的.

1.2 马尔科夫链

马尔科夫模型是一种随机时间序列分析法.对每一个固定的时间t，函数x(t)是随机变量，则称x(t)是随机过程.当随机过程在时刻t=i所处的状态已知，过程在时刻t=i+1所处的状态只与ti时刻状态有关，而与ti时刻以前的状态无关，那么此随机过程即为马尔科夫链.马尔科夫模型是通过对事物不同状态的初始概率与状态之间转移概率的研究来预测事物未来状态的一种数学方法[10].灰色预测的残差具有随机性，从而满足马尔科夫链的使用要求.因此，运用马尔科夫过程对灰色预测的初步结果进行残差修正具备理论的可行性.

1.3 灰色马尔科夫建模

1.3.1 建模原理

设有原始时间序列，满足条件X(0)(k)≥0,k=1,2,…，n,则可以通过如下步骤实现GM(1,1)的建模.

记原始序列为：X(0)={X(0)(1),X(0)(2),…,X(0)(n)}

1)原始时间序列一般都具有随机性，不能直接用于建模，有时可能需要对其进行平滑处理.对原始序列X(0)做一阶累加生成，能将随机序列转化为单调增长序列.

X(1)={x(1)(1),x(1)(2),…,x(1)(n)},

(1)

2)检验生成序列X(1)的准指数规律性

(2)

当k>3时，生成序列X(1)的σ(1)(k)∈[1,1.5]，则生成序列X(1)的准指数规律满足建模条件，此时才能对原始序列的生成序列X(1)建立灰色预测模型.

3)建立灰色预测模型

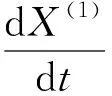
(3)

其中，a是白化系数，它反映了序列的发展态势，a∈[0,1]；u为内生控制灰数.

4)利用最小二乘法拟合得到系数向量

(4)

其中YN=[x(0)(2),x(0)(3),…，x(0)(n)]T,

5)求解微分方程，得到灰色GM(1,1)预测模型的时间响应公式

(5)

6)对式(5)做一次累减生成，还原出原始序列X(0)的预测值

(6)

7)马尔科夫残差修正模型

设家纺流行色预测误差的变化是个随机过程，记为Zn(n=1,2,…，N),误差所处于状态为En，对于N和所有的状态E1、E2、…、EN，当前状态Ei的概率只与前一个状态Ei-1有关，且状态发生转移是随机的，因此，可以用状态转移概率矩阵来描叙所有的状态转移可能性.在所有状态下，Pij(i,j=1,2,…，n)排成的矩阵为

根据灰色模型的初步预测结果，可获得历年预测结果的相对误差，然后将相对误差划分为几个状态区间，确定转移矩阵，便可根据某一年份所处状态来预测下一年份可能出现的状态，再对各个状态所处区间范围进行加权平均.设初始时刻的状态概率向量为S(0)=(P1,P2,…，Pn),则下一时刻的系统分布为S(1)=S(0)*P,依此类推，可得到k时刻系统所处的状态向量为S(k)=S(0)*Pk，这样就可以利用概率向量的值进行加权运算，进而得到马尔科夫模型残差修正值以及最终预测值.

8)模型检验

检验GM(1,1)模型的精度，一般采用后验差检验.后验差检验是根据模型预测值与实际值之间的统计情况进行检验的方法，这是从概率预测方法中移植过来的.以残值ε为基础，根据各期残差绝对值的大小，考察残差较小的点出现的概率，以及与预测误差方差有关指标的大小.计算过程如下：

设历史序列为x(0)(k)，预测值序列为

则可得后验差检验的二个重要指标值，即后验差比值C，小误差概率P，且

(7)

(8)

指标C越小越好，表明尽管历史数据很离散，而模型所得的残差值并不太离散，即模型对实际值的逼近程度越好.指标P越大越好，表明残差与残差平均值之差小于给定值0.675S2的点较多，即预测值分布越均匀.根据C与P两个指标，可以综合评定预测模型的精度，如表1所示：

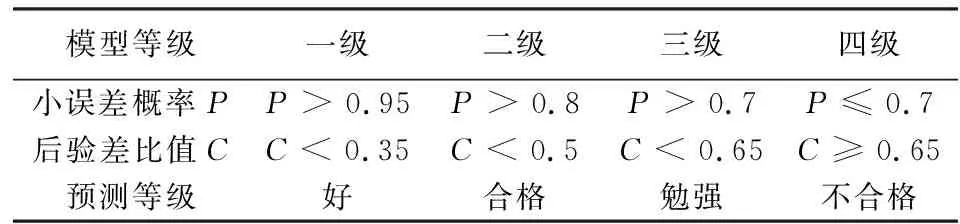
表1 灰色GM(1，1)预测模型等级评价Tab.1 Level evaluation of grey GM (1, 1) prediction model

1.3.2 预测方案设计

灰色建模过程中所选用的数据对象不同，得到的模型参数也就不同，建立的灰色预测模型不一样，这其实是灰色预测模型对特定条件下系统内在规律的反映.色彩作为家纺产品设计过程中的重要元素，它有其固有的特点：季节性和延续性.近年来家纺流行色的色彩趋势由10种色相成份所领航，分别是绿黄色、黄色、黄红色、红色、红紫色、紫色、紫蓝色、蓝色、蓝绿色、绿色.因此，首先以国际流行色权威机构国际色彩委员会发布的2007-2013年的春夏流行色定案为分析对象，得到所有色彩中各个色相成份历年所占的市场份额[11-12].为了强化原始序列的大致趋势，削弱原始序列中异常值的影响，即随机性过大，还需要对统计分析的结果进行平滑处理，得到适合建模的初始数据.然后选取连续5年春夏季度蓝色经过平滑处理之后的市场份额序列建立灰色预测模型.图1描述了对蓝色进行灰色马尔科夫预测的流程.

图1 灰色马尔科夫预测流程图Fig.1 Forecast flow chart of Grey-Markov model

第一步，以蓝色2007-2011年春夏季度的市场份额作为原始序列，并对原始序列进行平滑处理，检验其是否满足建模条件，然后应用满足建模条件的序列进行建模，得到预测模型.平滑处理的计算公式如下[13]：

k=2,3,…，n-1.

(9)

对于两端点的计算可采用如下公式：

(10)

(11)

第二步，以蓝色2012年春夏季度的市场份额作为模型精度的检验数据，应用P和C来评定模型的精度等级，并通过计算得到2012年春夏季度蓝色的市场份额预测值与实际值之间的相对误差.

第三步，剔除2007年的数据，增加2012年的数据，构建2008～2012年新的数据序列.按照第一步与第二步的顺序构建新的模型，对2013年春夏季度蓝色的市场份额进行预测.

第四步，依次类推，直到实现对2014年春夏季度蓝色的市场份额预测.

第五步，根据历年预测结果的相对误差建立马尔科夫残差修正模型，来对各个预测值进行修正，形成最终的预测值.

灰色马尔科夫预测模型对流行色的预测是逐个进行的，同样可以采用相同的流程来对其它色彩下一年春夏季度的市场份额进行预测.

2 实验案例分析

2.1 采用GM(1，1)预测

以国际流行色权威机构国际色彩委员会发布的2007～2013年的春夏流行色定案作为数据来源，选取了其中的蓝色作为建模对象，按照上述预测方案进行具体建模.2007～2013蓝色春夏季度市场份额的原始数据如表2所示.

表2 2007～2013蓝色春夏季度市场份额Tab.2 Market share of blue in the spring and summer quarter for the year of 2007～2013

模型对2012～2014年蓝色春夏季度的市场份额进行预测的结果如表3所示.

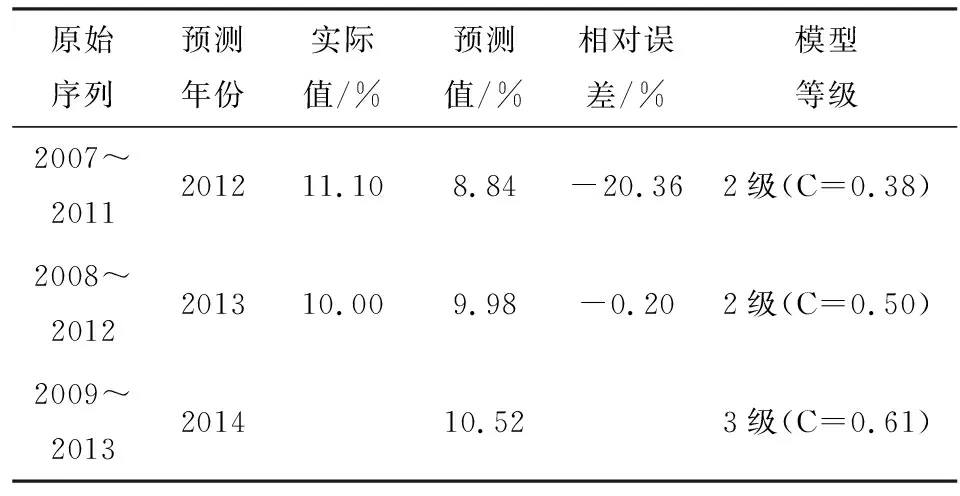
表3 GM(1,1)预测结果

由表3可知：上述各个原始序列建立的灰色模型等级基本上都是三级及以上，只有2009～2013年原始序列建立的灰色模型等级为三级，说明灰色建模能够及时补充最新信息，进行动态建模，对环境、参数等随机的非线性干扰具有一定的自适应能力.因此，对蓝色进行灰色建模是符合建模要求的.

2.2 马尔科夫模型进行残差修正

根据灰色模型的初步预测结果，可获得历年预测结果的相对误差，然后将相对误差划分为几个状态区间.

1) 相对误差在-53%至-21%之间，表示预测值被严重低估，称为状态1.

2) 相对误差在-21%至-0%之间，表示预测值被正常低估，称为状态2.

3) 相对误差在0%至21%之间，表示预测值被正常高估，称为状态3.

4) 相对误差在21%至53%之间，表示预测值被严重高估，称为状态4.

历年的预测结果如表4所示.

表4 GM(1，1)预测值、残差以及状态划分Tab.4 GM(1,1) prediction results,residual and state division

对应的状态转移概率矩阵为

实验以2011～2013年春夏季度的原始数据为测试数据，用以检验修正模型的改进效果.由表4可知，初始状态向量S0=[0 0.5 0.25 0.25]，从而可以得到2011～2013年的预测状态向量如表5所示.

表5 2011～2013年春夏季度蓝色预测状态向量Tab.5 Prediction state vector of blue in the spring and summer quarter for the year of 2011～2013

利用马尔科夫残差修正模型对2011～2013年的蓝色市场份额预测值进一步修正，可得最终预测值如表6所示.

表6 灰色模型与灰色马尔科夫模型预测结果对比Tab.6 Comparison of predicted results between grey model and Grey-Markov model

由表6可以看到，经过马尔科夫残差修正模型修正之后，虽然2011年预测误差变大了，但是对2012与2013年的预测精度都有所提高.这说明了灰色马尔科夫预测模型对于家纺流行色的趋势预测相比单一的GM(1,1)具有更好的趋势外推能力，更适合用于家纺流行色的长期预测.

3 结 论

本文提出了基于灰色马尔科夫模型的家纺流行色趋势预测研究.以国际流行色权威机构国际色彩委员会发布的2007-2013年的春夏流行色定案为分析对象，采用灰色模型对未来家纺流行色-蓝色的市场份额进行预测，并且通过后验差检验法来探讨此模型的预测精度及其建模的可行性，最后，应用马尔科夫模型对灰色预测的初步结果进行残差修正.实验结果表明，灰色马尔科夫模型在流行色趋势预测方面相比单一的灰色模型具有更好的趋势外推能力，更适合用于家纺流行色的长期预测，且预测精度更高.研究中还存在以下一些不足：1) 创新性和继承性是家纺产品流行色设计的基本原则，在今后的研究中应该通过增加对春夏、秋冬季节定案的分析与预测，获得对家纺流行色周期变化理论的验证和应用指导，以便于建立完整的家纺流行色预测体系；2) 家纺流行色受到多种复杂因素的影响，基于历史数据的家纺流行色预测研究只是对现象的预测，并没有深入到把握影响流行色发展趋势的本质，从而对其进行本质的预测.在今后的研究中，应该增加对影响因素与流行色内在关联的量化研究，以达到家纺流行色预测体系的智能化，真正做到精度预测.