基于双重扰动与改进教与学优化算法的DNA微阵列集成分类
陈 涛
(陕西理工大学 数学与计算机科学学院,汉中 723000)
DNA微阵列技术是分子生物学领域一项高通量测序技术,在一次实验中可以同时测试细胞中成千上万个基因活性,使得对单基因的研究进入到基因组学研究时代.其中,基于DNA微阵列的数据挖掘成为生物信息学领域研究热点之一,对生物医学发展具有重要意义[1,2].然而,微阵列具有高维、小样本及高冗余等特点,易出现维数灾难和过拟合等问题,使得神经网络、支持向量机及贝叶斯等机器学习方法不能很好地解决微阵列的数据挖据问题.
近年来,“集成学习”被成功地用于微阵列数据挖据,其最大优势是:一个基分类器的错分可以被其他基分类器的正确分类所抵消而达到一种平衡,从而降低选择到性能较差分类器的风险,同时提高集成分类器的性能.Krogh 等[3]指出:增加基分类器之间的差异性和基分类器的个体精度是提高集成学习性能的关键所在.此后,Bagging、Boosting、随机子空间、随机森林和旋转森林等一系列集成方法被提出,并取得较好的效果.但是,这些方法集成了所有基分类器,导致以下问题:(1)多个分类器的存储需要消耗大量计算机内存;(2)对多个分类器的输出进行集成需耗费大量计算时间,降低了算法的运行效率;(3)参与集成的基分类器数量越多,其之间的差异性容易受到影响,从而降低集成系统的泛化性能.
2002年,周志华等[4]提出的选择性集成学习有效的解决以上问题,主要是从训练的所有基分类器中选择部分分类器进行集成而获得更好的分类效果,从而有效地解决了集成分类中内存消耗大、运行效率低及集成性能受限等问题.此后,选择性集成分类方法受到广大研究者的关注,陆续提出一系列选择性集成方法,如周志华等[4]采用遗传算法实现选择集成;Martinez等[5]采用启发式规则提出基于精确度的选择性集成方法;Bryll等[6]采用改进的粒子群算法实现基分类器选择;Castro等[7]采用人工免疫算法进行选择性集成;Li等[8]使用聚类算法构建选择性集成.其中,基于遗传算法、粒子群和人工免疫等启发式智能优化算法构建选择性集成是一种有效方法.
教与学优化算法(TLBO)[9]是2011年Rao等提出的一种基于自然的启发式群体智能优化算法.其主要思想是通过教师的“教”和学生之间的互相“学”,提高学生整体学习水平.与其他智能优化算法相比,TLBO最大优势在于不需要设置过多参数.智能优化算法参数设置是一件比较困难的事情,且算法参数往往对于算法性能影响较大,但目前没有较好的参数选择的方法或原则,这给智能优化算法的广泛应用带来一定局限.正因此,TLBO算法以其自身独特的优点被广泛应用于各种优化领域,取得较好的优化效果.然而,TLBO算法也因为种群多样性过早丧失而易陷入局部最优,导致优化精度不高以及算法搜索速度较慢等不足[10].
本文提出了一种新的集成分类方法,首先基于bootstrap和邻域互信息的双重扰动机制产生训练子集并训练基分类器,这将增加基分类之间的差异性和提高基分类器的个体精度;然后设计了改进的教与学优化算法实现基分类选择性集成;最后通过微阵列数据集上的仿真实验来验证算法的有效性.
1 邻域互信息模型
邻域互信息(NMI)是在互信息概念的基础上,将邻域引入Shannon熵理论,实现对变量之间的线性或非线性关系进行度量.邻域互信息可以直接处理连续型数据,有效地避免了互信息使用过程中进行离散化而带来的信息损失问题,因而对微阵列数据的属性约简更加有效[11].
定义设样本集U={x1,x2,…,xn},属性集F={f1,f2,…,fm},属性子集R,S⊆F,则R和S之间的邻域互信息定义为:
其中,δR(xi)、δS(xi)和δRUS(xi)分别表示在属性子空间R、S和RUS中样本的邻域.

算法1 基于前向贪心搜索策略和邻域互信息的属性约简算法
2 改进的教与学优化算法
2.1 教与学优化算法TLBO
TLBO算法是一种基于自然的启发式智能优化算法,其主要思想是通过教师的“教”引导学生学习,同时学生之间进行互相“学”习,最终提高学生整体学习水平.TLBO算法由教师的“教”和学生的“学”两个过程组成,“教”是让学生向教师学习,而“学”则是学生之间进行互相学习.其中,“教”使得每个学员都向教师学习,向班级中的最优者靠近,搜索速度较快.但正因为过早地向教师靠近,导致种群多样性的过早丢失,易陷入局部最优;“学”使学生互相学习,取长补短,优于学员在彼此之间小范围内学习,不会过早地向全局最优方向凝聚,一定程度上保持了种群多样性,保证算法的全局搜索性能.
TLBO算法最大优势是不需要设置过多参数,且具有原理简单、易理解、优化效果相对较好等优点,被广泛应用于各种优化领域.
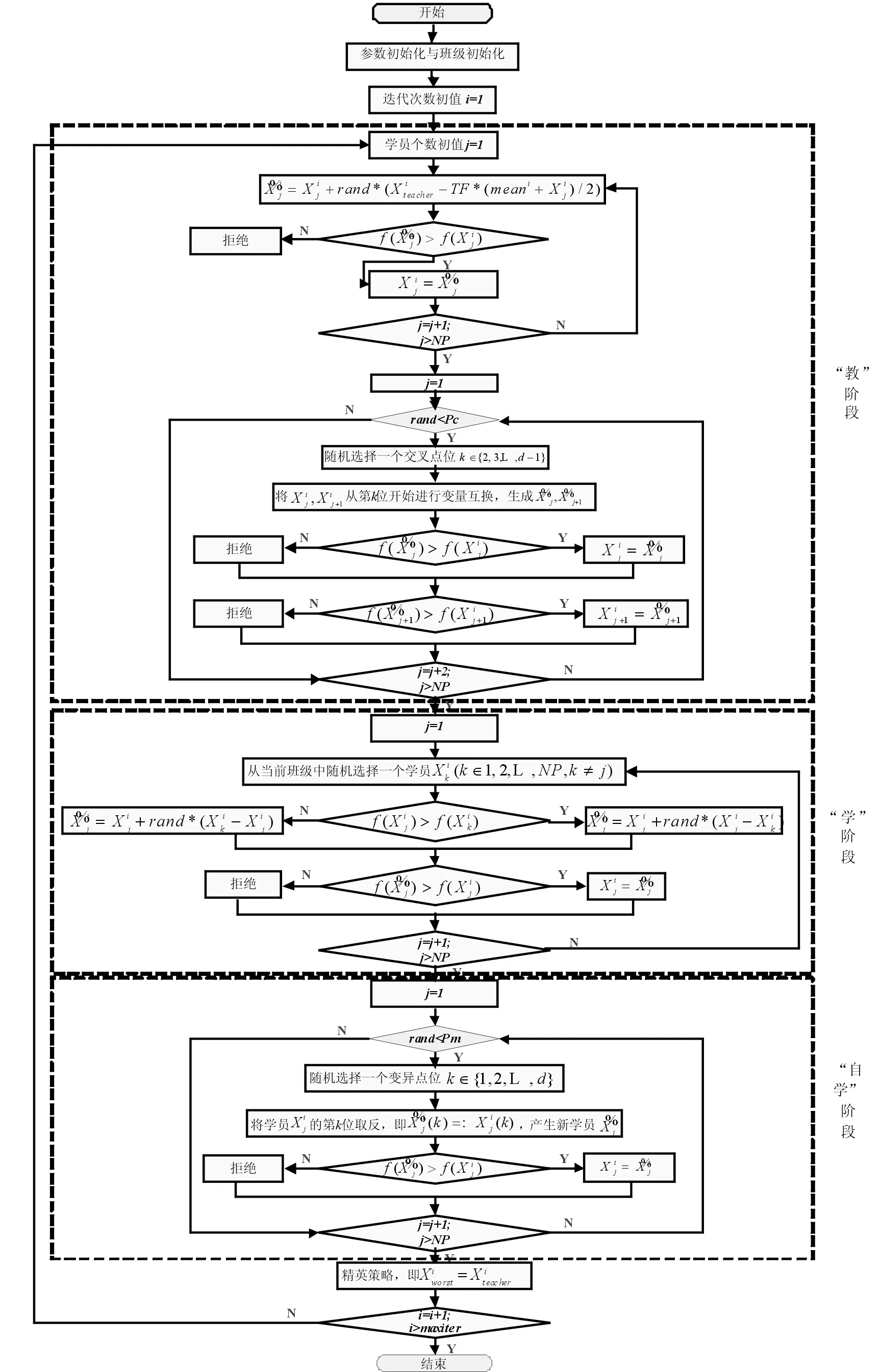
2.2 改进的教与学优化算法MyTLBO
TLBO算法也存在种群多样性过早丧失而易陷入局部最优、优化精度不高以及搜索速度较慢等不足[12],本文从以下三方面对算法进行改进,提出MyTLBO算法.
(1)“教”阶段改进
forj=1:NP
TF=round(1+rand(1,D));
end
2)“教”使得学员全部向教师学习,这样过早地向班级中最优个体聚集,虽能加快搜索速度,但往往导致种群多样性的过早丧失,易陷入局部最优.此处,借鉴遗传算法的“交叉”思想,在“教”之后,加入交叉操作,能把群体保持在合适区域内的同时,搜索新的解空间.
forj=1:2:NP
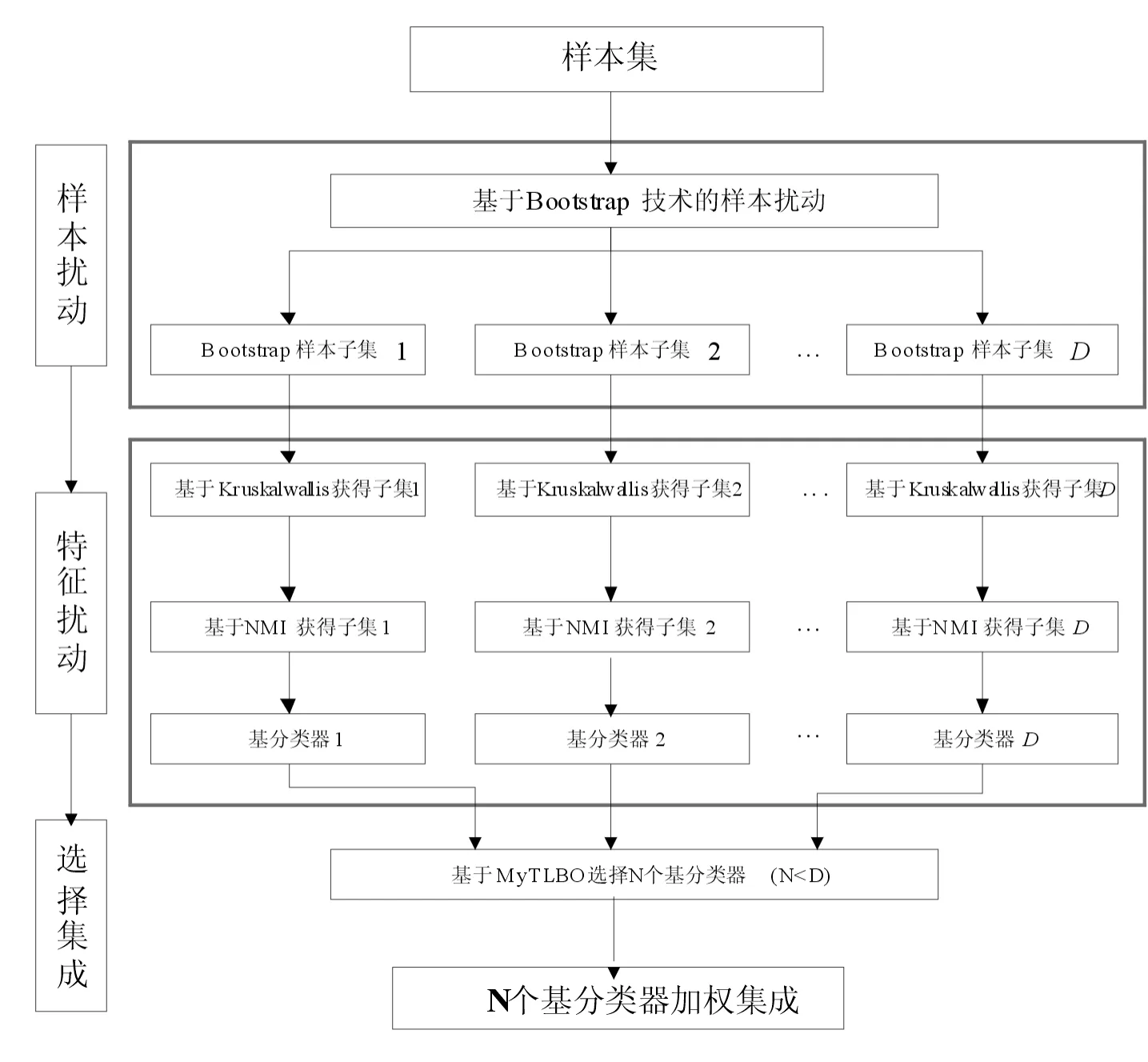
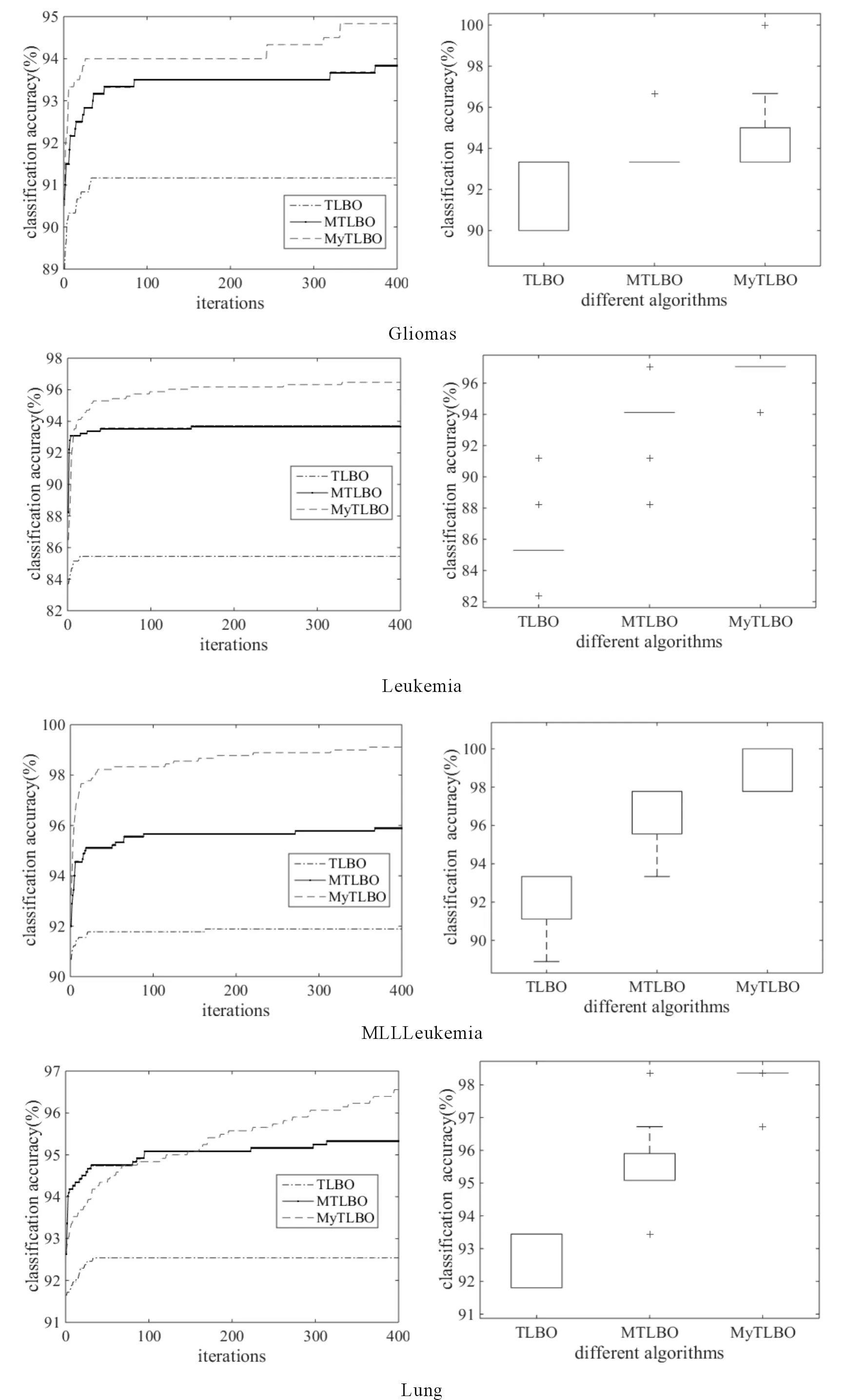
ifrand 随机选择一个交叉点位k∈{2,…,D-1}; end end (2)“自学”阶段改进 学员主要通过“教”和“学”两个过程进行学习,但没有考虑到个体自身学习,过分依赖他人,缺乏主观能动性和学习积极性.此处,借鉴遗传算法中“变异”操作使学员进行“自学”,获得更优解. forj=1:NP ifrand 随机选择一个变异点位k∈{1,…,D}; end end (3)精英策略 每代优化之前,选择种群中最好个体作为精英解,当种群经过一次优化后,用精英解替换当前种群中的最差解,保持最优解遗传到下一代,增强算法的收敛性能. 改进的教与学优化算法MyTLBO流程图见图1所示. (1)个体向量表示 班级中的学员被表示成一个由“0”和“1”组成的向量,代表从当前基分类器集中选择部分分类器组成的一个序列,如“010…101” ,其中“1”表示对应位置分类器被选,“0”表示对应位置分类器未被选中. (2)适应度函数构造 选择基分类器的目的是使得选择到的基分类器构成的集成分类器具有更高的分类精度,所以,算法中以分类精度作为评价学员水平的标准,即在训练集上采用交叉验证方法获得的平均分类精度作为适应度函数,其适应度值越大,则分类精度越大. 图1 改进的教与学优化算法MyTLBO流程图Fig.1 The flow chart of the improved TLBO algorithm 本文提出一种新的集成分类方法,整体框架如图2所示,具体步骤如下: (1)基于双重扰动样本集的方法训练产生基分类器.一方面,通过bootstrap技术实现样本扰动获得具有差异性的训练子集;另一方面,利用Kruskalwallis和邻域互信息方法进行属性约简实现特征扰动,既可加大训练子集之间的差异性,又通过属性约简剔除噪声,有助于提高基分类器的个体精度. (2)基于改进的教与学优化算法(MyTLBO)实现基分类器的选择性集成.针对教与学优化算法容易造成种群多样性过早丢失而陷入局部最优,设计了一种改进的教与学优化算法(MyTLBO)实现基分类器的选择性集成. 图2 本文算法的整体框架Fig.2 The overall framework of the algorithm 为验证本文算法有效性,采用公共微阵列数据集进行仿真实验,具体描述见表1. 表1 DNA微阵列数据集 为验证本文算法有效性,Bagging,AdaBoost,Ensemble 1(Bootstrap+Kruskalwallis+NMI),Ensemble 2(Bootstrap+Kruskalwallis+NMI+TLBO)和Ensemble 3(Bootstrap+Kruskalwallis +NMI+MTLBO) 等5种算法与本文算法进行对比,其中MTLBO[13]是Rao提出的一种优化精度和收敛速度较高的TLBO改进算法. TLBO、MTLBO和MyTLBO参数设置:班级规模为20,最大迭代次数为400,所有基分类器总数为40,Kruskalwallis预选基因数为300. 每个实验均重复20次,取20出实验结果的平均值为最终结果,可以排除试验结果的偶然性,其结果更具有一般性,更具说服力. (1)不同算法分类精度和分类器数量的比较 表2比较了不同算法的分类精度和基分类器的数量.很容易发现: 1)本文算法在所有数据集上的分类精度明显优于其他算法,至少分别被提高1%、2.79%、3.22%和2.7%,说明基于双重扰动和改进教与学优化算法构建的选择性集成分类系统具有明显优势.另外,与Ensemble 2和Ensemble 3比较,说明本文提出的MyTLBO比TLBO和MTLBO更有效,优化精度更高. 2)Ensemble 1在所有数据集上的分类精度明显优于Bagging和AdaBoost,至少分别被提高3.33%、20.7%、13.34%和3.34%,说明本文采用Bootstrap与Kruskalwallis及NMI的双重扰动方法,既增强分类器之间的差异性,又提升分类器的个体精度,有效地提升集成分类器的泛化性能.另外,本文算法、Ensemble 2、Ensemble 3与Bagging,AdaBoost、Ensemble 1对比发现,选择性集成是提高集成分类器精度的有效方法. 3)本文算法最终用于集成的基分类器数量在所有数据集上分别平均为13、5.85、14.1和6.5,远远小于40,表明仅用较少的分类器进行集成就可以获得更高的分类精度,既减少内存占用,又提高集成系统的泛化性能,再次证明选择性集成的效果明显. 表2 不同算法分类精度比较(%)Tab.2 Comparison of classification accuracy with the different algorithms(%) (2)TLBO、MTLBO和MyTLBO算法性能比较 表3对比了TLBO、MTLBO和MyTLBO算法构建的选择性集成器的分类精度,表中avg表示各算法在4个数据集上分类精度的平均值. 表3 TLBO、MTLBO和MyTLBO算法性能比较Tab.3 Performance comparison of TLBO、MTLBO and MyTLBO 从表3发现,无论是最优值、平均值和最差值,基于MyTLBO构建的本文算法分类精度明显优于MTLBO和TLBO设计的集成方法.特别从avg值来看,MyTLBO算法的最优、平均和最差分类精度相比其他算法至少提高1.39%、2.43%和3.4%,说明MyTLBO算法具有更强的收敛性和全局搜索能力,明显优于MTLBO和TLBO算法. 图3绘制了TLBO、MTLBO和MyTLBO算法的平均进化曲线图和多次试验统计盒图. 图3 平均进化曲线图和统计盒图Fig.3 The average evolutionary curve and statistical box chart 1)优化精度与速度比较 从图3看出,MyTLBO算法在所有数据集上的优化精度高于TLBO和MTLBO.TLBO容易陷入局部最优点,主要是因为迭代初期,班级成员均向教师聚集,导致种群多样性过早丧失而陷入局部最优.MTLBO算法因为增加了种群多样性,更容易跳出局部最优,寻找全局最优解.但从图中发现,MTLBO算法在迭代次数达到一定次数后,也因为种群多样性的丢失而陷入局部最优,所以MTLBO算法也很难搜索到全局最优解.MyTLBO算法既增强了种群多样性,使得迭代初期能保证较大的搜索范围,而不至于陷入局部最优;同时变异操作提升了种群的局部搜索能力,所以进化曲线随迭代次数的增加不断阶梯型递增,保持了更强的全局和局部搜索能力,保证了全局最优解的获得. 还发现,MyTLBO的搜索速度明显比MTLBO和TLBO快,即在迭代次数较小时就能达到与MTLBO、TLBO同样的优化精度,甚至更高. 2)算法稳定性比较 图3显示了三种算法20次实验结果的统计盒图.可以发现,除Gliomas,MyTLBO算法在其他数据集上的稳定性明显好于TLBO和MTLBO算法. 综合分析,MyTLBO算法相比MTLBO和TLBO算法,具有优化精度高、搜索速度快和稳定性好等优势,说明本文提出的MyTLBO算法是有效的、具有一定的优越性. (3)基于统计学理论比较算法性能 从表4看到,Bagging、Adaboost、Ensemble 1、Ensemble 2和 Ensemble 3等算法与本文算法的几何平均正确率r分别是0.8807、0.8836、0.9521、0.9710和0.9889,表明本文算法明显优于其他5种算法;从s统计量看,本文算法在所有数据集上结果均优于其他算法;从“平均”值看,本文算法的平均精度为97.11%,远优于其他算法. 进一步得到这些算法优劣排序依次是:本文算法、Ensemble 3、Ensemble 2、Ensemble 1、Adaboost和Bagging. 本文提出了一种新的选择性集成分类方法,该方法基于Bootstrap技术和Kruskalwallis与NMI属性约简方法实现数据集的双重扰动,增加基分类器之间的差异性和准确性,然后采用改进的教与学优化算法构造选择性集成分类器.仿真实验表明:本文算法在分类精度、稳定性等方面具有较强的优势.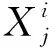
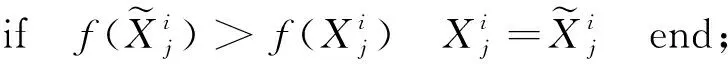
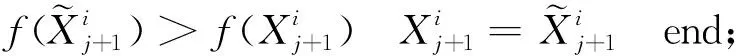
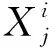

2.3 个体向量表示与适应度函数构造
3 本文算法
4 仿真实验
4.1 实验数据

4.2 实验方法与参数设置
4.3 实验结果及分析


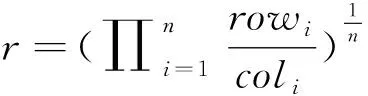
5 结语

