基于双窗口区域激励的边缘提取算法

廖义德,雷小舟,杨 凯，杨晓东

(武汉工程大学 机电工程学院，武汉 430205)

边缘提取是图像处理中的较为基础的问题之一，被广泛地应用在图像分割、模式识别、图像、图像加密[1]等领域. 在图像的边缘提取领域，较为传统且使用率较高的做法是使用梯度算子来实现，通常有Sobel, LoG,以及Canny，这些算法实现起来较为简单，但是存在一些问题. 如Sobel算法处理后的图像虽然一致性较好，但是提取出来的边缘可能较粗，因此无法提取出局部细节丰富的边缘图像；LoG和Canny在实际运用过程中，由于参数对环境的依赖性较强，所以对环境的适应性较差，而且产生的图像边缘可能不连续以及可能存在伪边缘. 因此，研究人员不断提出新的算法思想来解决图像的边缘提取问题. Mallat[2]等提出了利用小波卷积核来计算图像梯度的方法，通过求小波核函数的导数来求取图像梯度，计算过程相对稳定. Ren等[3]提出了将光强和内部色差融合的边缘提取算法，能获得更多的图像边缘信息. Ortiz等[4]提出了基于双色反射模型的彩色通道耦合分析来提取图像的边缘信息，其算法结构简单，对计算能力要求较低，且对噪声和图像光强变化不敏感. Drogoul等[5]提出了将拓扑梯度法应用于各种噪声和模糊图像的边缘检测和去噪，通过计算穿孔、裂纹域以及每个噪声模型的拓扑梯度来实现图像的边缘提取，实验表明此方法具有有效性、鲁棒性和快速性. 张捷等[6]提出了一种用于边缘提取的细胞神经网络(cellular neural networks，CNN)模板的设计方法，该方法通过将模拟退火粒子群算法与细胞神经网络结合来提取图像的边缘信息. 杨婷等[7]提出了基于像素空间分布的阈值自适应忆阻细胞神经网络方法来提取彩色图像的边缘信息，通过利用新型非线性两端电路元件忆阻器来解决 CNN 的硬件实现难题，并且提高了细胞神经网络在彩色图像边缘提取的自适应能力，具有良好的抗噪性.

可以看出，对于边缘提取这个图像处理中的经典问题，学者们进行了大量的研究. 本文通过将双窗口区域信息引入Sigmoid函数来获得图像的边缘信息，算法流程简单，性能稳定，通过设置不同环境下的多组实验表明，该方法可以提取出图像的边缘信息.

1 原理介绍

传统的微分边缘检测算法由于采用较为单一的图像像素点来进行微分计算，因此获得的信息较由一个像素点为中心的区域信息来说要少[8]. 通过引入区域信息，可以获得单个像素点为中心的周围区域内的综合信息，通过将这些信息加以利用，可以获得更为丰富的边缘信息. Etiene Vincent等[9]提出了一种函数，通过判别当前像素点是属于目标还是背景能够用来描述区域信息. 孙根云等[10]受Etiene Vincent算法的启发，提出设置Sigmoid 函数来传递该像素点所在区域的信息来检测图像的边缘，该方法原理简单，性能稳定，但是对于明暗不一致的情况适应性较差. 孙根云等设置的Sigmoid函数具有以下形式：

(1)

ω(x,y)=t(I(x,y)-Imean(x,y)),

(2)

式(1)中，ω(x,y)代表对比函数，用来表示区域内的综合信息；式(2)中，对于(x,y)处像素点，其灰度值为I(x,y)；以其为中心的某区域的像素平均值为Imean(x,y)；t为数值变量，也可设置为t=Imax(x,y)-Imin(x,y)，其中，Imax(x,y)及Imin(x,y)分别代表区域内的最大值与最小值. 通过采用如上的Sigmoid函数和对比函数ω(x,y)，孙根云等成功地提取出了模糊医学图像的边缘，且边缘宽度比较细. 但对于明暗不一致的图像，效果一般，为了弥补这个缺陷，与孙根云等提出的算法不同的是，本文采用的原理如下.

对于(x,y)处像素点，其灰度值为I(x,y)，设置以其为中心的双窗口区域分别为Ω1，Ω2，采用正方形或者圆形，双窗口大小分别为m，n，(m≠n≠0)，为正方形边长或圆形直径；窗口内的灰度平均值分别为IΩ1，IΩ2. 设置如下所示的Sigmoid函数以及对比函数ω(x,y).

(3)

(4)

式(3)中，Sigmoid输出的激励值范围为[-1,1]，而图像的有效显示区域为[0,1]，因此对于[-1,0]所在区间内的激励值设置为背景. 式(4)中，ε代表防止分母为0的极小数值常量，如10-9。

通过设计如上的双窗口区域的局部灰度均值的比值来消除光照的影响.

在实际的计算过程中，除了可以直接输出Sigmoid激励值以外，还可以采用如下的计算方法来输出当前像素点为中心的所在区域的总激励，以获得更丰富的边缘信息.

设置当前像素点为中心的所在区域为Ω3，窗口大小为k，总激励为Ss，其中

(5)

在实验中进一步发现，采用如下计算方法可以使输出图像的对比度有所提高.

设窗口参数大小为m，n，k对原图按照式(3)～(5)计算产生的总激励值为S(m,n,k)，相应的有S(n,m,k). 其中S(m,n,k)≠S(n,m,k)，代表意义不同，数值可能相同，不同是因为对比函数ω(x,y)中提到的区域灰度值发生了分子分母颠倒. 因此，将两者结合，计算综合灰度值Sc来获得高对比度图像.

(6)

为了获得更快的计算速度，也可设置为

Sc=|S(m,n,k)|+|S(n,m,k)|.

(7)

因为窗口的大小会影响边缘的宽度，当选择较大窗口时，边缘会随之变宽，因此实际使用过程中需要针对不同的对象选择合适的窗口大小. 除此之外，仍然存在图像对比度偏低的问题，通过引入对比度算法如自适应直方图均衡化算法(AHE)来提高图像的对比度[11].

具体算法步骤如下：

a) 输入图像并进行归一化；

b) 选择合适的窗口数值，即m,n,k值；

c) 按式(3)(4)计算Sigmoid激励值；

d) 按式(5)计算总激励Ss，结果保存为R1；

e) 对结果R1按式(6)或式(7)计算综合灰度值Sc，结果保存为R2；

f)对结果R1，R2进行图像对比度增强，分别获得结果R3，R4，人工比较结果R3，R4，选取两者中边缘提取效果较好的结果图像.

2 实验

为了验证本文方法的有效性，设计了多组实验，其中的一些实验结果如下所述. 如图1为光强分布严重不均匀的路标图像.

从图2～6的结果分别可以看出，Sobel算法的结果获得了较为完整的路标边缘，但砖块的边缘细节不够完整；LoG算法和Canny算法则存在明显的细节丢失，尤其是存在边缘线段不连续以及伪边缘的问题；孙根云等的算法对光照敏感，产生了大量的噪声和伪边缘，路标的外轮廓边缘几乎完全与伪边缘重叠. 本文算法产生的结果中路标边缘线段连续完整，而且能够保留足够多的砖块边缘细节. 除此之外，相比于LoG算法和Canny算法，本文算法仅有3个窗口的大小参数需要调整，其余采用固定的形式. 在这里，设定窗口大小为分别为m=4,n=8,k=8. 因参数不存在小数，故参数调整较LoG算法和Canny算法要方便. 而且本文提出的方法在一定程度上弥补了孙根云等提出的算法的缺陷，即对于明暗分布不一致的图像，能够准确的提取其边缘信息.

图1 受光强污染的路标Fig.1 A road sign with unevendistribution of light intensity图2 Sobel算法提取结果Fig.2 Algorithm results of Sobel 图3 LoG算法提取结果Fig.3 Algorithm results of LoG图4 Canny算法提取结果Fig.4 Algorithm results of Canny图5 孙的算法提取结果Fig.5 Algorithm results of Sun图6 本文算法提取结果Fig.6 Algorithm results of this paper

对于光照不均的情况，本文方法和Sobel算法明显优于LoG、Canny以及孙根云等的算法. 为了更全面地比较本文方法与Sobel算法之间的优劣性，另外考虑了两种情况，一种是背景复杂，局部细节丰富的图像，如图7所示的100美元图像，一种是模糊边缘的医学图像，如图8所示的人体头颅X光照图片.

图7 100美元图像Fig.7 100 dollar image

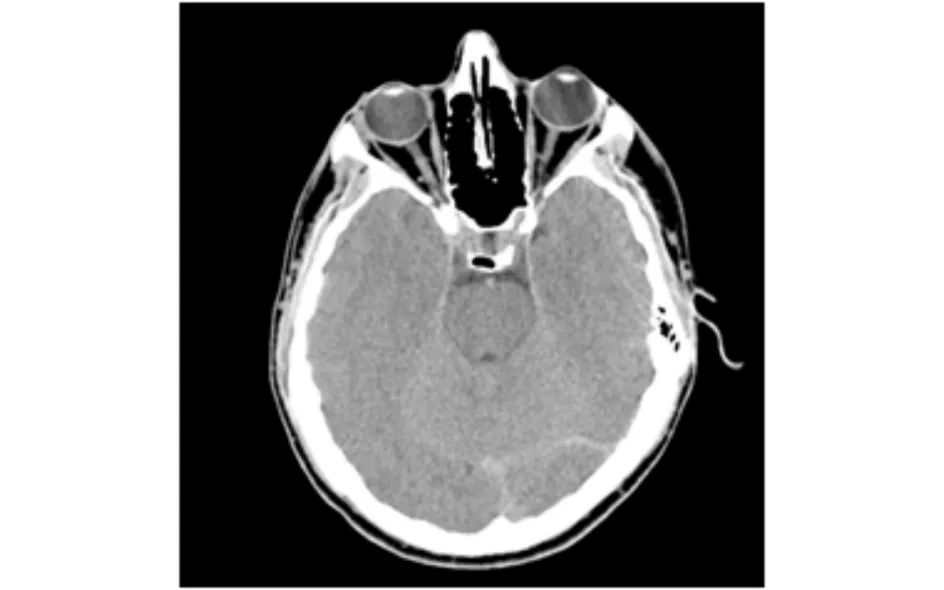
图8 人体头颅X光照图Fig.8 X ray image of human head

对于如图7所示的100美元图像，Sobel及本文方法边缘检测结果如图9～10所示.

图9 Sobel算法结果Fig.9 Results of Sobel algorithm

图10 本文算法结果Fig.10 Algorithm results of this paper

图10中，算法参数设置为：m=4,n=2,k=2. 从图9和图10对比可以看出，Sobel算法产生了较粗的边缘，且人物头像两侧的椭圆圈以及100字符两侧的花纹基本被白化带淹没(白化带的宽度可以用来形容边缘的宽度)，因此，对于椭圆圈以及花纹的边缘提取，Sobel算法并不理想.本文方法产生的白化带宽度较之Sobel算法要细，且100字符两侧的花纹清晰可见. 因此，此种环境下，本文方法产生的边缘的宽度质量比Sobel算法的效果要好，且在细节方面明显优于Sobel算法.

对于图8所示的具有模糊边缘的人体头颅X光照图片，Sobel算法及本文方法产生的结果分别如图11～12所示.

此处，参数设置为：m=4,n=2,k=2. 从图11中可以看出，对于这种具有模糊边缘的人体头颅X光照图片，Sobel算法产生的结果由于白化带较宽，存在边缘重叠现象，如头颅的外轮廓线以及左右两侧模糊区域. 因此，其边缘提取的结果不理想. 而本文方法虽然对比度没有Sobel算法高，但产生的白化带较窄，边缘较细，且可以明显地区分出头颅的外轮廓线及左右两侧模糊区域，因此，此种环境下，本文方法优于Sobel算法.

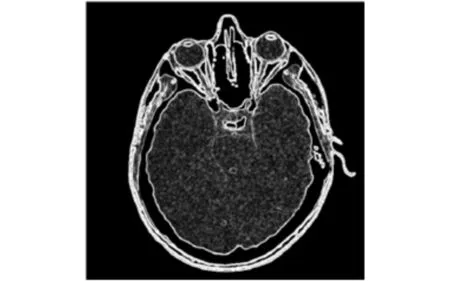
图11 Sobel算法结果Fig.11 Algorithm results of Sobel

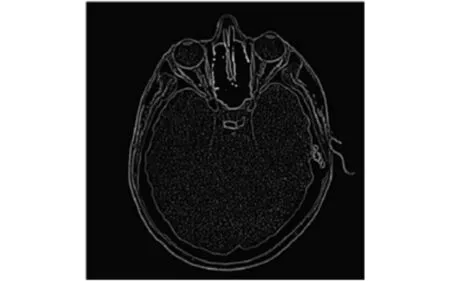
图12 本文方法结果Fig.12 Algorithm results of this paper

3 结语

3种不同环境下的实验可以看出，对于光照分布不均且边缘明显的图像，本文方法与Sobel算法都能获得较好的边缘检测结果.由于本文提出的方法引入了双窗口局部灰度均值的比值来度量边缘的显著程度， 与LoG、Canny以及孙根云等的算法相比，能更好地适应光照的变化. 在与Sobel算法的全面比较后发现，对于背景复杂、局部细节丰富及边缘较为模糊的图片，本文方法较Sobel算法处理后的效果更好，边缘宽度更细且局部细节更加丰富.因此，本文提出的方法具有一定的通用性，而且计算过程简单，性能稳定，具有一定的实用价值.