基于数字测高仪和GPS观测的三亚地区电离层-等离子体层总电子含量特征分析

罗伟华，何 康,朱正平

(中南民族大学 电子信息工程学院，武汉430074)

无线电波传播路径上单位截面柱体里的积分电子含量即总电子含量(TEC)是表征电离层特性的一个重要参数.为计算TEC，通常可利用数字测高仪观测和地基全球导航定位系统(GPS)观测[1-4].通过数字测高仪观测，可得到电离层电子密度随高度的分布，进一步可反演出当前时刻60～1000 km范围内电离层的总电子含量. GPS卫星距离地面高度约为20200 km，通过GPS观测可解算出0～20200 km范围内的总电子含量.GPS卫星在与地面通信时，无线电波会穿过电离层和等离子体层，利用GPS观测得到的TEC不仅包括了电离层的总电子含量还包括了等离子体层的总电子含量，等离子体层的总电子含量对信号的影响也需要考虑，即等离子体层的总电子含量是不能忽视的.结合电离层数字测高仪和GPS观测可得到约1000～20200 km范围内的TEC，而20000 km以上区域的电子密度太小对于整个等离子体层的贡献较小，可以忽略不计[5]，故由GPS观测得到的总电子含量(GTEC)与数字测高仪反演得到的总电子含量(ITEC)之差可近似认为是等离子体层的总电子含量[6](PTEC).对于等离子体层总电子含量的分布特征，已有少量研究.如Lunt等[7]利用GPS和NIMS卫星观测数据反演得到的总电子含量，发现在太阳活动强烈时等离子体层的总电子含量对整个TEC的贡献最高可达到50%.种小燕等[8]结合非相干散射雷达和GPS的观测资料发现Millstone Hill(42.6°N，288.5°E)地区等离子体层总电子含量在太阳活动低年(2005，2008年)的值约为3～7 TECU，在太阳活动高年(2000，2002年)的值约为4～14 TECU.张满莲等[9]利用COSMIC低轨卫星2008年的观测数据反演出等离子体层的总电子含量，发现等离子体层的总电子含量存在明显的经度变化，且不同经度链上的等离子体层的总电子含量存在不同的季节变化特征.当前对我国低纬地区(18°N)的相关研究还相当少.此外，当今国际上通用的电离层模型，如国际电离层参考模型[10](IRI)通常只包含了电离层的总电子含量，而很少考虑等离子层的总电子含量，因此通过对等离子体层总电子含量的特性研究，能进一步完善等离子体层总电子含量模型，还能对一些实际应用的误差修正提供一定的参考.本文将利用2012年海南三亚台站(18.34°N，109.62°E)数字测高仪和GPS的观测资料对等离子体层的总电子含量的变化特征进行分析.本文结果可为构建等离子体层模型奠定理论基础，具有一定的科学意义.

1 数据来源及数据处理

通过电离层数字测高仪获得电离层高度随探测频率变化的分布图，可以得到F2层峰高以下的底部电离层电子密度分布；F2层峰高以上的电离层电子密度分布，可利用α-Chapman方程反演计算[2]得到：

(1)

(2)

式(1)和式(2)中，NmF2、hmF2分别表示电离层F2峰值电子浓度和F2层峰高，HT表示标高，Ne(h)表示高度h位置上的电子密度.结合底部和顶部电离层电子密度分布可得到整个电离层的电子浓度剖面图，然后通过积分运算得到电离层的积分电子含量：

(3)

其中s表示60～1000 km的高度范围.通过上述方法得到的电子含量可以认为是电离层的总电子含量即ITEC.

GPS通过计算卫星发射出的无线电波信号的载波相位延时，比如可以通过差分群延时、差分载波相位、法拉第旋转等方法得到较为精确的斜向TEC[11].为了减小多路径效应带来的影响，我们选取了仰角大于25°的斜向TEC(STEC，定义符号NSTEC)，通过引入电离层薄层模型[4]，将STEC转化为天顶角方向上的垂直TEC(VTEC，定义符号NVTEC)：

(4)

NVTEC=NSTEC·cosχ,

(5)

式(4)和式(5)中，χ为天顶角，Re为地球半径，h为薄层高度，为400 km，α为卫星仰角.再通过估算并剔除硬件延迟得到总电子含量即GTEC.

由于20000 km以上区域的电子密度太小，对整个等离子体层的贡献较小，可以忽略不计， 故PTEC可认为是GTEC与ITEC的差值。为进一步分析GTEC与ITEC之间的关系，在本文中还计算了每月和每个时刻的GTEC与ITEC差值的均方根误差：

(6)

当计算每月的均方根误差时，n为24，xi和yi分别代表当月在时刻i的GTEC和ITEC的月均值；当计算每个时刻的均方根误差时，n为12，xi和yi分别代表当前时刻第i月的GTEC和ITEC的月均值.

2 GTEC与ITEC的比较分析

图1给出了2012年1～12月的月平均GTEC与ITEC的日变化特征.图中横坐标为世界时(地方时LT=UT+8)，纵坐标为GTEC和ITEC，时间间隔为1 h，图中的短竖线表示标准差.从图1中可以看出，由GPS导出的TEC与测高仪导出的TEC的变化特征一致，均表现出显著的日变化特征.极大值点出现在1400～1600 LT，极小值大约出现在0500 LT附近.春秋两季(春季为3～4月，秋季为9～10月)的GTEC和ITEC的最大值相对较高，夏冬两季(夏季为5～8月，冬季为11～2月)相对较低. GTEC月均值日变化极大值在50～75 TECU范围内，在10月达到最大(约75 TECU)，ITEC月均值日变化的极大值在40～58 TECU范围内，在10月达到最大(约58 TECU)这与我国广东、海南地区的TEC变化特征一致[12].

图2给出了2012年1～12月期间GTEC与ITEC关系对比散点图，图中横坐标代表ITEC，纵坐标代表GTEC，图中直线为GTEC与ITEC的最小二乘拟合的结果.从图2中可以看出相关系数平方约为0.88，这意味着GTEC与ITEC有良好的相关性.从拟合截距可知GTEC与ITEC之差平均值大约为7.5 TECU，这与已有的一些研究结果大致是相同的，如Belehaki等[3]在2000年10月至2001年9月期间得到雅典台站(38°N，23.5°E)此截距约为6.2 TECU. Makinnell等[13]在2005年3～6月期间南非Grahamstown台站(22.2°S，26.5°E)得到此值约为3.75 TECU.

图1 2012年1～12月，月平均GTEC与ITEC的日变化特征.深色线表示GTEC，浅色线表示ITECFig.1 The daily variation of the monthly average values of GTEC and ITEC during 2012. Dark line represents GTEC, Light color line represents ITEC

图2 2012年1～12月期间，GTEC与ITEC散点关系图Fig.2 Scatter plot of GTEC against the corresponding ITEC during the period January to December 2012

为进一步研究GTEC与ITEC的关系，图3给出了2012年1～12月每月的GTEC与ITEC的散点关系图.图中横坐标代表ITEC，纵坐标代表GTEC，直线表示最小二乘拟合的结果.

图3 2012年1～12月，GTEC与ITEC散点关系图Fig.3 Scatter plot of GTEC against the corresponding ITEC of each month in 2012

从图3中可以看出，在不同月份，相关系数平方均大于0.8，在冬季月份可达到0.95，说明GTEC与ITEC的逐月数据均有很强的相关性.夏季月份的拟合截距在10 TECU左右，且最大值不超过14 TECU.冬季月份的拟合截距在6 TECU以下.春季月份和秋季月份的拟合截距在5～10 TECU变化.

图4给出了每个月GTEC与ITEC的均方根误差和每个时间点的GTEC与ITEC的均方根误差，RMSE根据式(6)计算得出，横坐标分别为月份和世界时，纵坐标为均方根误差.

图4 2012年每月的GTEC与ITEC均方根误差(a)与不同时刻的GTEC与ITEC均方根误差(b) Fig.4 RMSE for each month (a) and each moment (b) between GTEC and ITEC

从图4(a)可以看出，GTEC与ITEC的均方根误差均小于14 TECU.其中冬季月份均方根误差较小，在10 TECU以下，夏季月份均方根误差在10 TECU左右，而在春季月份和秋季月份均方根误差较大，均超过10 TECU.从图4(b)可以看出GTEC与ITEC的均方根误差在0600～2200 LT时间段大于10 TECU，其他时间均小于10 TECU.在1900 LT前后达到最大值15 TECU.均方根误差的日变化趋势呈日出时分较小，然后逐渐增大，且在日落时分达到最大后逐渐减小.这说明利用α-Chapman反演得到F2峰值以上电离层电子浓度的方法是可靠的.

3 等离子体层总电子含量的变化特征

基于GTEC和ITEC的定义，GTEC和ITEC的差值可以认为是等离子体层的电子含量.图5给出了2012年1～12月月平均PTEC的日变化图，其中横坐标为世界时，纵坐标为PTEC，短竖线为标准差.从图5中可以看出，PTEC的极大值出现在日落前后，极小值出现在日出前后，冬季月份的PTEC在3～15 TECU范围内变化，在5月和9月最大值能达到22 TECU.

图6给出了2012年每个月PTEC占GTEC的百分比月平均值变化图，其中横坐标为世界时，纵坐标为PTEC占GTEC的百分比，短竖线为标准差.从图6中可以看出夜间的百分比要明显高于白天，白天普遍不高于30%，而在5月和12月0500 LT可以达到80%.

结合图1、图5和图6，可以明显看出在0800-1200 LT范围内，GTEC与ITEC的差值(即PTEC)很小，均不超过5 TECU，大部分在1～3 TECU甚至有的不到1 TECU，而且PTEC占GTEC的百分比也很小，大部分在10%以下，甚至接近0.因此，在精度要求不高的情况下，可忽略在这个时间范围内的PTEC差值.

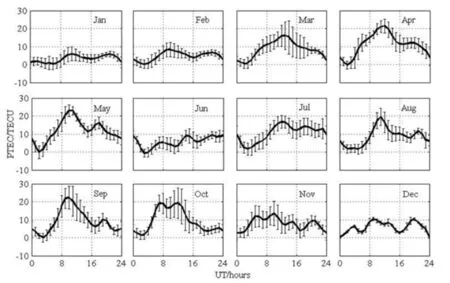
图5 2012年1～12月，月平均PTEC的日变化特征Fig.5 The daily variation of the monthly average values of PTEC for 2012

一般认为，在白天，电离层的电子含量迅速增大，使电离层有一部分电子向等离子体层输送，同时等离子层电子复合加快，导致等离子体层电子含量增大.在晚上，电离层电子含量迅速减小，等离子体层有一部分电子向电离层输送以维持夜间F2层，同时等离子层电子复合变慢，等离子体层电子含量减小[2].电离层的电子含量基数大、复合反应快等原因相对于等离子体层电子含量变化较大，虽然相互之间会有一部分的电子输送，但因等离子体层电子含量变化太小，导致等离子体层电子含量所占百分比在白天比夜间要低.

4 结语

本文利用三亚地区数字测高仪和GPS2012年的观测资料，比较了由GPS观测得到的总电子含量和数字测高仪反演得到的总电子含量，并进一步计算了等离子体层的总电子含量，对等离子体层电子含量的日变化特性、占总的电子含量百分比的日变化特性和随季节的变化规律进行了分析.具体结果可总结如下：

(1)电离层的总电子含量表现出显著的日变化特性，白天值较高，夜间值较低，在0500 LT前后最小，在1400～1600 LT左右达到最大. GTEC与ITEC的变化趋势相同，两者相关性很高，全年数据相关系数平方为0.88，各月相关系数平方都在0.85以上，冬季月份相关系数平方在0.95左右.

(2)等离子体层电子含量具有明显的日变化，从0800 LT前后开始上升，1800 LT前后达到最大后开始下降.等离子体层电子含量白天之值明显高于夜间.

(3)等离子体层电子含量占总的电子含量百分比也存在显著的日变化特性，在白天的占比值明显高于夜间的占比值，且每月月平均占比值均在0500 LT左右达到最大，月平均占比值的最大值在55%～80%范围内变化，其中12月的占比值可达到80%.

(4)等离子体层电子含量在北半球低纬地区冬季月份相对较小，春秋两季相对较大.冬季月份的PTEC在3～15 TECU范围内变化，在5月和9月最大值能达到22 TECU.

由于本文仅分析了一年的观测资料，等离子体层的有些特征可能并未完全揭示.更多地区和更长时间跨度的观测资料有待于进一步积累以开展更深入研究.

致谢本文所用数据均来自于中科院地质与地球物理研究所，在此表示感谢.

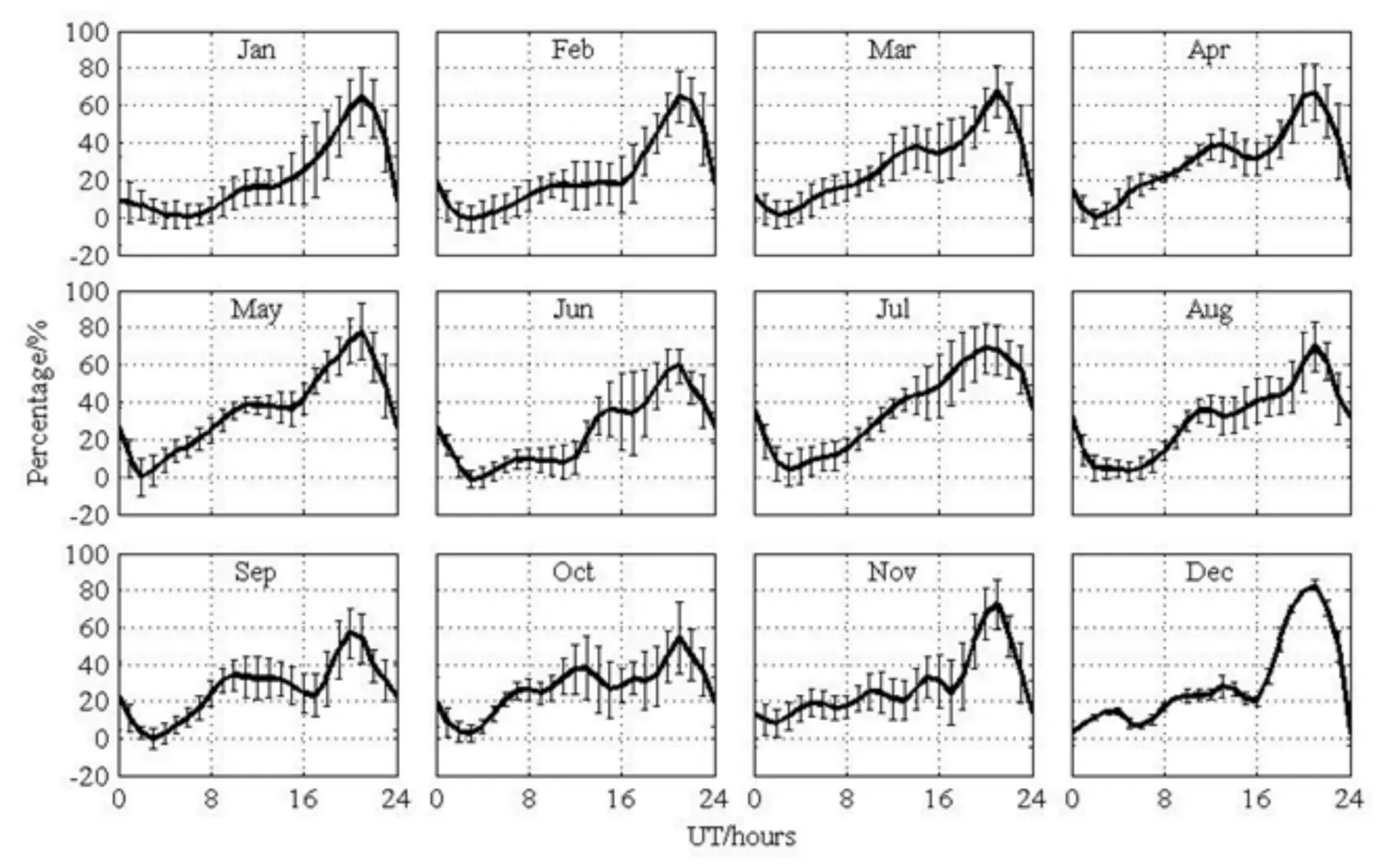
图6 2012年1～12月，月平均PTEC占GTEC百分比的日变化特征Fig.6 The daily variation of the monthly average values of the contribution of PTEC (to GTEC) during 2012