基于核密度估计的飞行高度层识别

谢春生，李少华

（中国民航大学空管学院，天津300300）

飞行轨迹是为航空器运行划设的“空中高速公路”，是连接机场与机场网络的纽带。随着信息技术和空间数据库技术的发展，大量快速存取记录器（QAR，quick access recorder）数据可直观显示航班运行的空域环境、管制员指挥习惯、飞行员操作习惯和飞机性能等信息，是“人机环”相互作用的综合体现[1]。近年来，碳交易市场的开放，使提高运行品质、加强航空公司节能减排技术的开发成为研究热点，而飞行高度层优化是提高飞行安全品质、降低飞行成本的一种有效措施。因此，从海量庞杂的历史飞行轨迹中识别出盛行飞行轨迹可为优化飞行高度层提供科学依据，具有非常重要的意义。

目前，国内外关于最佳飞行高度层的研究方法主要集中在以下方面。在管制适应性方面，优化飞行高度层可成为增加空域容量、降低管制员工作负荷的一种有效手段。牟奇锋等[2]提出在管制指挥过程中使用航空器飞行高度层指派，利用垂直剖面航迹进行优化。李诚等[3]从航路容量出发，建立航路交叉点处的最优高度层分配模型，同时，利用航空器在航路上运行的成本指数，建立0-1整数规划模型。在飞机性能优化方面，提升飞机性能、降低飞行成本。罗嘉[4]以飞行管理系统为依托，利用飞行力学原理优化飞行轨迹，阐述飞行管理系统的前景。张鲁红[5]采用改进粒子群算法实现飞行轨迹垂直剖面的优化，基于飞行轨迹优化的性能指标，分别构建了爬升段、下降段及巡航段的适应度函数。在航空公司安全经济适应性方面，提高航班飞行计划准确性也是优化飞行高度层的一个重要出发点。赵雷通[6]从飞行计划角度出发，提出经济飞行优化模型，研究优化航空运营直接运行成本的方法。

以上研究主要存在以下不足：飞行轨迹依托理论模型建立，与实际运行存在很大差异，然而飞行轨迹剖面是复杂因素的综合体，只从单一角度出发具有一定的局限性，将理论研究应用到实际航班运行值得商榷。因此，很难完全满足航班飞行高度层优化的实际运行需求。

对上述研究分析的基础上，首先，建立飞行轨迹间差异距离的计算模型，通过Hausdorff距离来定义两条轨迹之间的距离，采用核密度估计方法计算概率密度。然后，利用模拟退火算法搜索出最大的概率密度，该最大概率密度值对应的轨迹即是盛行飞行轨迹，分析该轨迹对应的飞行高度层，从而得到最优飞行高度层。最后，以某公司ZGNN-ZSNJ航班为例，快速、有效地识别盛行飞行轨迹，分析最优飞行高度层，结果表明该方法具有一定的可行性。

1 基于核密度估计的飞行轨迹识别

1.1 飞行轨迹定义

QAR数据可以记录飞机运行所处的大气环境以及飞机自身运动特征。一般情况下，QAR记录的周期为1 s，飞行轨迹Trj{p}则由QAR记录的一系列表征飞行特征的离散点组成，每一个离散点pi表征在某时刻t，航空器在第i点的位置、航向、速度、大气温度等信息，可表示为

其中：N、E和H为航空器在该空间位置的纬度、经度和高度坐标；heading为航向；V为飞机的真空速；T为大气温度。因此，飞行轨迹可表示为

其中，n表示飞行轨迹的离散点总数。飞行轨迹模型如图1所示，撤轮挡点为起点，挡轮挡点为终点。

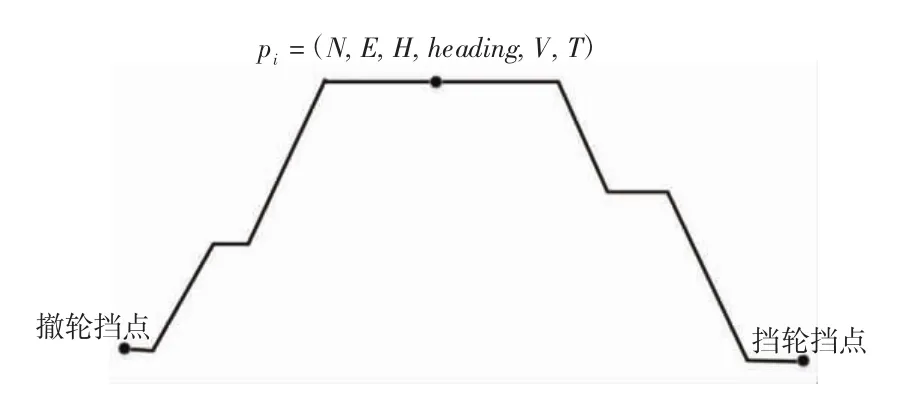
图1 飞行轨迹示意图Fig.1 Flight path diagrammatic sketch

1.2 轨迹间差异距离计算模型

飞行轨迹簇是指多条起点与终点一致的飞行轨迹组合，取该飞行轨迹簇作为样本参数，而盛行飞行轨迹表示飞行轨迹簇中最能代表大多数轨迹特征的一条轨迹。盛行飞行轨迹不仅可表示该航段运行受管制干预的影响情况，也是飞行高度层优化设计的重要参考。

为了快速准确地识别盛行飞行轨迹，揭示轨迹之间的差异和规律，以此表征航班运行特征，拟采用概率密度估计方法，获取最大概率密度值，则该最大概率密度值对应的轨迹即是盛行飞行轨迹。

轨迹之间的差异距离是确定概率密度估计的关键。由于轨迹由众多的航迹离散点组成，则定义轨迹间的差异距离是一个关键问题，这直接影响概率密度估计的准确性[7]。在历史研究中，距离的计算方法有多种，如欧式距离、切比雪夫距离、夹角余弦距离等。由于飞行轨迹数据是空间运行数据，其度量单位的不统一性及数据之间的无关联性使得这些距离的计算方法无法作为飞行轨迹差异距离的计算标准。通过分析发现，不同的飞行轨迹离散点个数不同，直接距离计算会出现计算距离异常增大的情况，对此应采用Hausdorff距离表征两个轨迹离散点之间的相似程度，距离的大小表明匹配程度的高低。

假设两个轨迹为

其中：pi={Hpi，Npi，Epi}；qj={Hqj，Nqj，Eqj}；Hpi、Hqj表示轨迹点的高度；Npi、Epi、Nqj、Eqj分别表示轨迹点的纬度和经度信息。则Trj{p}和Trj{q}之间的Hausdorff距离定义为

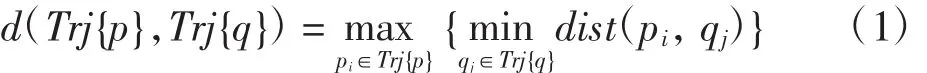
其中：pi、qj分别属于 Trj{p}和 Trj{q}中的轨迹离散点；dis（tpi，q）j表示pi与qj之间的欧式距离。

为方便表示n条轨迹之间的差异距离，建立差异度矩阵为

1.3 核密度估计概念

核密度估计[8]是由Rosenblatt等提出，又名Parzen窗，是非参数统计中非参数估计的一种方法。该算法不需要假设样本服从某种特征分布，同时，也不受模型参数设定的限制。大量的样本数据可使核密度估计逐渐收敛于某一概率密度。因此，采用核密度估计是处理大批飞行轨迹样本的一种有效方法，可求解出轨迹样本的特征分布函数。

假设样本D有n个样本点表示为

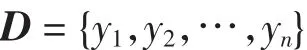
则核密度估计函数表示为

其中：K（·）为核函数；Hw为带宽。常用的核函数有均匀核函数、三角核函数、Epanechikov核函数、四次方核函数、三权核函数、高斯核函数、余弦核函数和指数核函数等。由于高斯核函数平滑性较好[9]，因此，该核密度估计的核函数采用高斯核函数，即

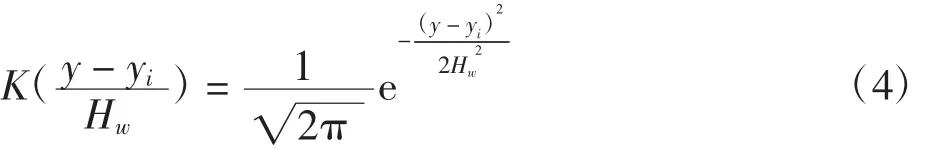
综上所述，将式（4）代入式（3），得到飞行轨迹簇的概率密度函数为

2 最优飞行高度层识别方法

飞行高度层是指以1013.25 hPa（1 hPa=100 Pa）气压为基准的一系列等压面，各等压面之间间隔一定的气压差。中国民用航空局按照东单西双的规则将各高度层相互错离。管制员将航空器分配在不同的高度层上，以此保证航空器之间存在规定的安全裕度，这是有效避免航空器与航空器之间、航空器与其他障碍物之间存在危险接近的重要措施[10]。根据实际飞行轨迹确定飞行高度层，需考虑实际运行情况下飞机性能及交通管制的干预。因此，识别最优飞行高度层可为仅依靠经验拟定飞行高度层提供科学依据，提高实际运行中制作飞行计划的准确性，避免因航班少加油存在的潜在安全隐患，或多加油引起的油耗增加，造成运行成本增加。

最优飞行高度层识别的方法可按如下步骤进行：

1）根据1.2节构造轨迹Trj{p}和Trj{q}之间的差异矩阵A；

2）根据式（5）进行核密度估计，计算核密度估计值；

3）采用模拟退火算法寻找最大概率密度值，可找到全局最优的概率密度点Den；

4）确定全局最优概率密度点对应的轨迹Trj{b}，即该轨迹为盛行飞行轨迹；

5）分析该飞行轨迹平飞航段的高度层及对应的经纬度坐标，确定转换点处经纬度坐标，则该点为飞行高度层转换点，对应的高度层为最优飞行高度层。

3 实例分析

以某公司2016年一年的执行ZGNN-ZSNJ航班的318条飞行轨迹为例进行分析，该数据未做任何处理，可真实反映该航段的实际运行情况。通过对该航班2016年1～12月的数据进行统计分析，具体如表1所示。根据民航航班运行周期，分为冬春航季和夏秋航季，规定冬春航季从每年10月至次年3月，夏秋航季从4月至当年10月。图2和图3分别给出了飞行轨迹二维图和三维图，其中，H为飞行高度（ft，1 ft=0.3048 m，下同）。

表1 2016年1～12月ZGNN-ZSNJ航班执行情况Tab.1 ZGNN-ZSNJ flight execution from Jan～Dec 2016

图2 飞行轨迹二维图Fig.2 Flight path 2D graph

图3 飞行轨迹三维图Fig.3 Flight path 3D graph

通过表1可看出，该航班全年10个月的飞行油耗执行率超过100%，因此航班在实际运行中存在安全隐患，通过分析该航班计算机飞行计划拟定的飞行高度层为FL311，因此需要针对该航班进行高度层优化分析。

首先利用Matlab软件计算318条轨迹点之间的Hausdorff距离，建立差异度矩阵A318×318，定义带宽Hw=5000，利用式（5）进行核密度估计，求解出飞行轨迹的核密度函数值。由于数据量过大，只给出部分飞行轨迹的核密度函数值，如表2所示。

采用模拟退火算法求得全局最优的概率密度点Den=34，则该概率密度点对应的飞行轨迹为盛行飞行轨迹，如图4所示。图5给出盛行轨迹三维图。

对最优飞行轨迹分析，第一平飞航段飞行高度层为FL266，第二平飞航段飞行高度层为FL291，高度层之间的转换点为VQ（大榕江），开始下降点为SAGUD。该航班因受管制干预，飞行高度层无法达到预设高度FL 311，因此最优飞行高度层为FL266 VQ FL291。

表2 部分飞行轨迹核密度函数值Tab.2 Kernel density function value of partial flight path

图4 飞行轨迹及盛行飞行轨迹Fig.4 Flight trajectory and prevalence filght trajectory

图5 盛行飞行轨迹三维图Fig.5 3D prevalence filght trajectory

表3 飞行高度层调整前后油量对比表Tab.3 Oil volume before and after flight level adjustment kg

通过表3可看出，最优高度计划飞行油量比预设高度计划飞行油量冬春航季多260 kg，夏秋航季多355 kg。根据2016年1～12月ZGNN-ZSNJ航班统计表可看出，高度层调整之后的计划轮挡油量比平均实际轮挡油量最少多286.79 kg，轮挡油耗执行率冬春航季最大为93.21%，夏秋航季最大为95.42%，可保证安全运行，同时减少油耗浪费。

4 结语

从海量庞杂的飞行轨迹中分析轨迹间空间特征和总体走向，利用Hausdorff距离方法定义两条轨迹之间的距离，建立轨迹间差异度矩阵。采用核密度估计方法计算概率密度函数值，利用模拟退火算法选取全局最大密度值，实现了盛行飞行轨迹的识别，分析盛行飞行轨迹的特征，定义最优飞行高度层。实例结果表明，该方法可快速有效地识别盛行飞行轨迹，同时定义的最优飞行高度层与预设飞行高度层相比，既可保证飞行安全，也可达到节能减排目的。