基于VOF方法的大水滴袋状破碎的仿真研究
张文英, 常士楠, 蒋 斌, 雷梦龙
(北京航空航天大学 航空科学与工程学院, 北京 100191)
0 引 言
冻雨的形成是由于大量存在于高空云顶的冰晶粒子或液态水滴在暖层中凝结下落,穿过较薄的冷层,由于高层大气缺少凝结核而未能发生相变,仍以液态水的形式存在。以冻雨或冻毛细雨形式存在高空中的大水滴(d>50 μm),我们称之为过冷大水滴(Supercooled Large Droplets,SLD)。
由于大水滴在空中较之地面的数密度和雨强贡献率较大,它对飞机表面的撞击结冰比常规尺寸的水滴危害更大[1]。研究常规尺寸的水滴可以忽略在运动中的形变和破碎,假设其始终为球形,且不会发生飞溅等现象。而大水滴由于直径较大,水滴的Oh数(Ohnesorge数)较小(通常远小于0.1),意味着水滴表面张力和内部粘性力的量级小于所受的气动力,这表征着在水滴撞击机翼表面前就会发生水滴的变形和破碎,并且在撞击飞机迎风表面后会发生飞溅,生成尺寸更小的子水滴,或将在未设防护的较大区域上发生二次撞击,出现不可控的结冰,危害飞机的安全飞行。由此可见过冷大水滴导致的飞机结冰现象较之常规水滴更为复杂,引起了各国研究人员的重视[2-14]。
围绕运动液滴的破碎与变形,国内外的研究人员倾注了大量的心血,并取得了一些重要的研究成果。国外对于大水滴的实验研究起步较早,Hinze[2]早在上世纪中期就开展了在高液-气密度比和高Re数条件下液滴破碎的研究,提出了在一定Oh数条件下,破碎模式随着We数改变而变化。Krzeczkowski[3]在Hinze的基础上进行了继续研究,确定了破碎模式和We数的对应关系,并且分析了典型的袋状和剪切破碎的形态特征。Chou和Faeth[4]做了在高液-气密度比和低Oh数(Oh≪0.1)条件下的液滴破碎的瞬态特性研究,提出了袋装破碎时间与水滴特征时间相关的结论。Rimbert和Castanet[5]认为可以用R-T不稳定性来解释袋状破碎的机理,或者是由于液滴内部的流动导致。Guildenbecher[6]对液滴破碎的实验文献做了综述,并且提出液滴袋状破碎的机理是其内部液体由两极向赤道位置的流动。
尽管在实验文章中,研究人员们已经给出相对可靠的破碎模式和We数对应的范围,但是由于测量技术的限制,难以得到流场中的压力分布和液滴内部的流动,因此水滴变形和破碎的机理尚未明确。伴随着计算机技术和图形学的发展,研究人员针对液滴的变形和破碎在数值仿真方面也取得了一定的成就。Zaleski[7]进行了大液滴在Re=1000条件下的数值仿真,追踪了相界面的细节变化和液滴变形处气流的涡流结构。Desjardins[8]、Lebas[9]、Sander和Weigand[10]各自做了液滴在不同We数条件下变形破碎的仿真研究,但是由于研究的重点不同,他们更关注的是直接数值仿真或者是大涡模拟的算法应用,在防冰以及大水滴的破碎等方面应用略显不足。
国内的相关研究主要以仿真为主。西北工业大学的胡剑平[11]以及上海交通大学的罗辉[12]等人侧重于应用现有的水滴动力学模型去仿真研究SLD对飞机部件结冰的影响。他们的研究结果证明了,考虑大水滴动力学特性的仿真结果相较于只考虑常规尺寸水滴更贴近实验结果,充分证明了研究大水滴运动变形的必要性。然而仅仅从宏观角度对水滴运动行为学进行研究,不能从机理上解释水滴变形破碎和飞溅的现象,因此,针对单个水滴的运动和变形破碎进行研究是很有意义的。在此方面,北京航空航天大学的常士楠课题组[13-14]做了关于水滴袋状、复合破碎过程中变形特性研究,对相关的理论模型进行了改进,实现了水滴变形量和破碎时间的预测。
本文应用VOF方法对不同韦伯数下的水滴进行数值模拟,关注两相界面变化,得到与实验一致的变化规律,应用R-T不稳定性解释袋状破碎现象;统计了水滴的变形、破碎时间和运动速度等瞬态特性,与前人的实验数据和理论模型加以对比,揭示其特性与原理。
1 数值方法与物理模型
在两相流的数值仿真方向,主要有两大类方法:界面追踪法(Interface tracking Method)和界面捕获法(Interface capturing Method),它们分别是基于拉格朗日和欧拉方法。前者将两相流其中一相视为大量微小粒子的集合,然而它的局限性在于不能自动修改拓扑结构,并且很难实现并行运算。而基于欧拉方法的界面捕获法,包括本文采用的VOF(Volume of Fluid)方法和LSM(Level Set Method)方法。VOF方法追踪每个网格内液体的体积分数,因此有着较好的质量守恒特性;但是,在两相界面陡峭的条件下,LSM方法能够更好地捕捉界面。但是LSM方法守恒性较差,随着数值迭代的积累,在界面变化时液体体积可能会丢失,并且它的计算开销较之VOF方法更大。综上所述,本文选择了VOF方法进行仿真。
本文的研究对象为相对于静止空气有较大的初速度的大水滴,由于与环境温差小并且液滴尺寸相对较小,在研究过程中可以忽略传热传质现象,湍流影响和重力作用[15],因此水滴运动变形的流场可以视为二维轴对称不可压缩的层流流场,求解相应的N-S方程和连续方程。动量方程的控制方程,即考虑表面张力项的N-S方程为:

式中F为液体体积分数,定义如下:

由F定义可知,式(1)中
ρ(F)=ρlF+ρg(1-F)(3)
ρl、ρg分别是液相和气相的密度。
同理可得
μ(F)=μlF+μg(1-F)(4)
式中μl、μg分别是液相和气相的动力黏度。u为速度矢量,t是时间,应变率张量由D=(u+uT)/2给出。式(1)中最后一项即为表面张力项,σ为表面张力系数,而κ为气液界面曲率,δs为表面狄拉克δ函数。
数值模拟的计算模型示意图如图1所示,流场为1.5×40 mm的矩形,x轴为轴对称条件,其他三个边界均为常压压力出口条件。初始条件为流场空气静止且为常温常压(20 ℃,一个大气压),一个直径为0.62 mm的初速度为u0的球形水滴出现在流场中,并从距入口1.5 mm处开始运动。

图1 水滴在静止空气中运动破碎示意图Fig.1 Schematic of a high-speed droplet movement and breakup in still air
影响水滴变形、破碎的参数主要有水滴初始直径d0,水滴-气流相对速度u,水滴-气流表面张力σ,水滴、气流的密度ρl、ρg,动力黏度μl、μg等。进行无量纲化后得到无量纲参数表达式如下:
We=ρgu2d0/σ(5)
Re=ρgud0/μg(6)

采用上述无量纲参数,可列出算例条件见表1。
由于VOF模型对于网格质量和密度的依赖性较强,本文选用了三套网格进行独立性验证。在水滴运动变形的区域网格尺寸分别是25 μm,10 μm和5 μm,网格数目分别是25万,60万和120万。验算表明,当网格尺寸较大时,液相界面较粗糙,不能准确把握变化迅速的水滴变形破碎的特征。但是当网格过密时,增加了大量的计算时间且计算结果没有明显的改善,综合比较之后,选择了最小尺寸为10 μm的网格进行计算。
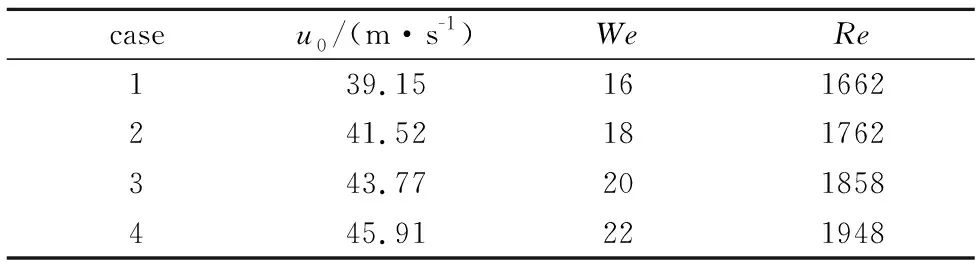
表1 算例初始条件设置(Oh=0.00473)Table 1 Summary of the simulation initial conditions (Oh=0.00473)
本文对压力耦合方程的求解采用了半隐方法,即SIMPLEC算法,在文献[19]中对二维层流流动的计算结果表明,SIMPLEC算法的收敛特性远优于SIMPLE算法。压强计算采用了PRESTO格式,其他物理量采用QUICK格式离散。
2 计算结果与分析
2.1 大水滴典型袋状破碎形态特征
在不同的We数下,液滴的破碎呈现出不同的形态特征,Guildenbecher[6]对这些破碎模式做了总结性的分类,它们分别是振动破碎、袋状破碎、复合模式破碎、剪切破碎和破坏性破碎。可以由表2看出,这些破碎类型之间并不存在We数的明确界限,不同的研究人员往往给出了不同的结果。这主要是因为目前对破碎模型的定义只是定性而不是定量的,并且由于实验条件的不同(激波管、风洞或者喷嘴),都对水滴破碎产生了较大的影响。
对于表1所列出的速度范围,即流体相对速度较低时,大部分数值分析选择了层流流动进行计算,此时对水滴破碎的分析往往基于不稳定性理论。对这一部分的分析往往考虑以下因素:表面张力作用(R-P不稳定性),水滴被环境空气加速/减速(R-T不稳定性),以及在液滴边缘表现出的剪切不稳定性(Kelvin-Helmholtz不稳定性,简称K-H不稳定性)[20]。最后一项常见于剪切破碎模式下的分析,本文暂不考虑。在对于非紊流袋状破碎的研究中,R-T不稳定性被广泛应用于解释实验结果[21-23],本文中也将R-T不稳定性应用于解释袋状破碎初期的现象。

表2 不同的液滴破碎模式We数范围划分(Oh数远小于0.1)Table 2 Different breakup regimes as a function of We(Oh is far less than 0.1)
因此,本文针对不同研究人员确定的袋状破碎区间,选择了We数为14~22的水滴,作为典型袋状破碎算例进行形态特征的分析和研究。如图2所示,可以观察到水滴在静止空气中以中等速度运动,并逐渐发生变形破碎的过程。从中可以明显地观察到破碎的典型特征和发生的时间,在接下来的章节中将对这些特征和各类重要的瞬态性能进行分析和研究。 在水滴破碎过程中通常使用特征时间tc来对各种瞬态性能进行无量纲化分析,tc的表达式如下:


图2 We=16水滴随时间变形破碎过程(水滴运动方向从左至右)各图对应无量纲时间为:t/tc=a) 0, b) 0.33, c) 0.55, d) 0.77, e) 1.22, f) 1.77, g) 2.12, h) 2.19.此处tc=452 μs.Fig.2 Numerical simulation for droplet moving from left to right with We=16 at t/tc=a) 0, b) 0.33, c) 0.55, d) 0.77, e) 1.22, f) 1.77, g) 2.12, h) 2.19. (tc=452 μs)
根据仿真中观察到的水滴变形和破碎的形态特征,本文首次提出,将袋状破碎分为五个特征阶段,具体如下:
1) 梯形变形阶段
图2(a-c)的过程,水滴由球形开始发生形变。由于水滴运动方向从左至右,在迎风侧的变化较为迅速,由图3(b)可见,水滴迎风侧靠近驻点的位置由于该处的高压被挤压变平。而与之相对应的,水滴在背风侧的变化较为缓慢,仍基本保持球体不变,这与早期的实验所观察到的现象一致[4]。此后由于惯性力和气动阻力的共同作用,水滴整体逐渐被挤压变平,在无量纲时间t/tc=0.55时,可以观察到明显的梯形结构。
2) 延伸发展阶段
图2(c-d)是水滴纵向延伸并且厚度均匀的阶段。由图3(c)可见,在运动前方驻点处和液体内部压力作用下,水滴在x方向受力逐渐被挤压。又由于水滴边缘处空气的速度增大,静压减小,水滴在y方向不断延展,最终形成了一个厚度均匀的圆饼形水滴。这个由球体逐渐变为扁平的过程在无量纲时间t/tc=0.77时,可以显著观察到。
3) 水环形成阶段
图2(d-f)是水环结构出现的阶段。水滴由厚度均匀的饼状向中心较薄边缘较厚的袋状结构发展,中部的液体向边缘移动,水环不断变厚并且作为支撑结构承力,在t/tc=1.77时可以明显观察到水环的形成。而水滴中心部位反速度方向延展,形成袋状薄膜。这主要是由于袋状凹陷处,气流在驻点处的高压区挤压液体在水滴内部由赤道位置向极点位置运动导致。并且由图3(e)可以看出,液滴的表面出现了压力波动,然而这些扰动还处在表面,由于袋状薄膜的厚度未达到临界值,这些微小的扰动没有穿透液滴。
4) 袋状破碎阶段
图2(f-g)是袋状结构不断向后延展变薄,最终破碎断裂与水环分离的过程。这个过程可以用R-T不稳定性来解释。R-T不稳定现象可以简单表述为:当两种不同密度流体的分界面做加速运动且加速度方向垂直于界面时,此界面是否稳定取决于加速度的方向是否从大密度流体指向小密度流体。由于受到气动阻力,并且水滴所受加速度方向由轻质流体(空气)指向重质流体(水),就会出现R-T不稳定现象,表现为袋状薄膜上出现压力的扰动,见图3(f-g)。
这个过程可以用R-T不稳定性来解释,如文献中所述[21],假定传统的二维不稳定性理论可以扩展至三维条件,根据R-T理论,可以证得在液滴表面出现特定波长的扰动时,扰动振幅的增长速度最快,这一特定波长见式(9):
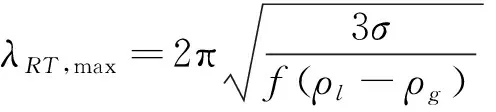
其中f是盘状液滴在静止空气中的加速度,其表达式如式(10)所示:
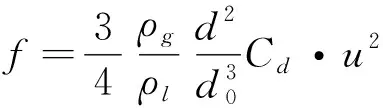
这种特定波长的扰动迅速在液滴的迎风面上形成并发展,扰动的幅度也逐渐增大,形成孔洞最终穿透液膜并迅速扩大.在无量纲时间t/tc=2.12时,可以观察到膜状结构破裂,与水环分离。
5) 子液滴回缩阶段
图2(g-h)是袋状薄膜破碎成更小的子液滴的过程。如图2(h)所示,可以观察到中心薄膜上和与水环相接处,均出现了正弦波的形状。
按照实验观测和R-P不稳定性的假设[20],受到恒定加速度作用的黏性流体在运动过程中会由于不稳定性诱导而破碎。即对于特定形状的流体,存在一个特征频率(fc)的扰动,这个扰动的周期(λc)一定而成长率最大,在运动过程中占据统治地位,导致流体发生破碎。
在这一假设条件下对实验和仿真结果进行分析:Jain[18]在液滴破碎实验中观察到子液滴的粒径呈双峰分布,分别是水环破碎和袋状薄膜破碎产生的,即袋状薄膜破碎后产生的子液滴粒径均一。此外,如图2(g)所示,本文仿真结果中同样观察到,临界破碎时薄膜表面出现的正弦波是等振幅的,与前文实验观察结论结合,可以由理论计算预测袋状破碎后子水滴的粒径分布。
在无量纲时间t/tc=2.19时,可见到断裂后的正弦周期状液面不断回缩,在表面张力的作用下呈表面积最小化的趋势,形成圆形液滴。此外,虽然袋状薄膜破碎,但外围的水环仍保持了原有形状不变。

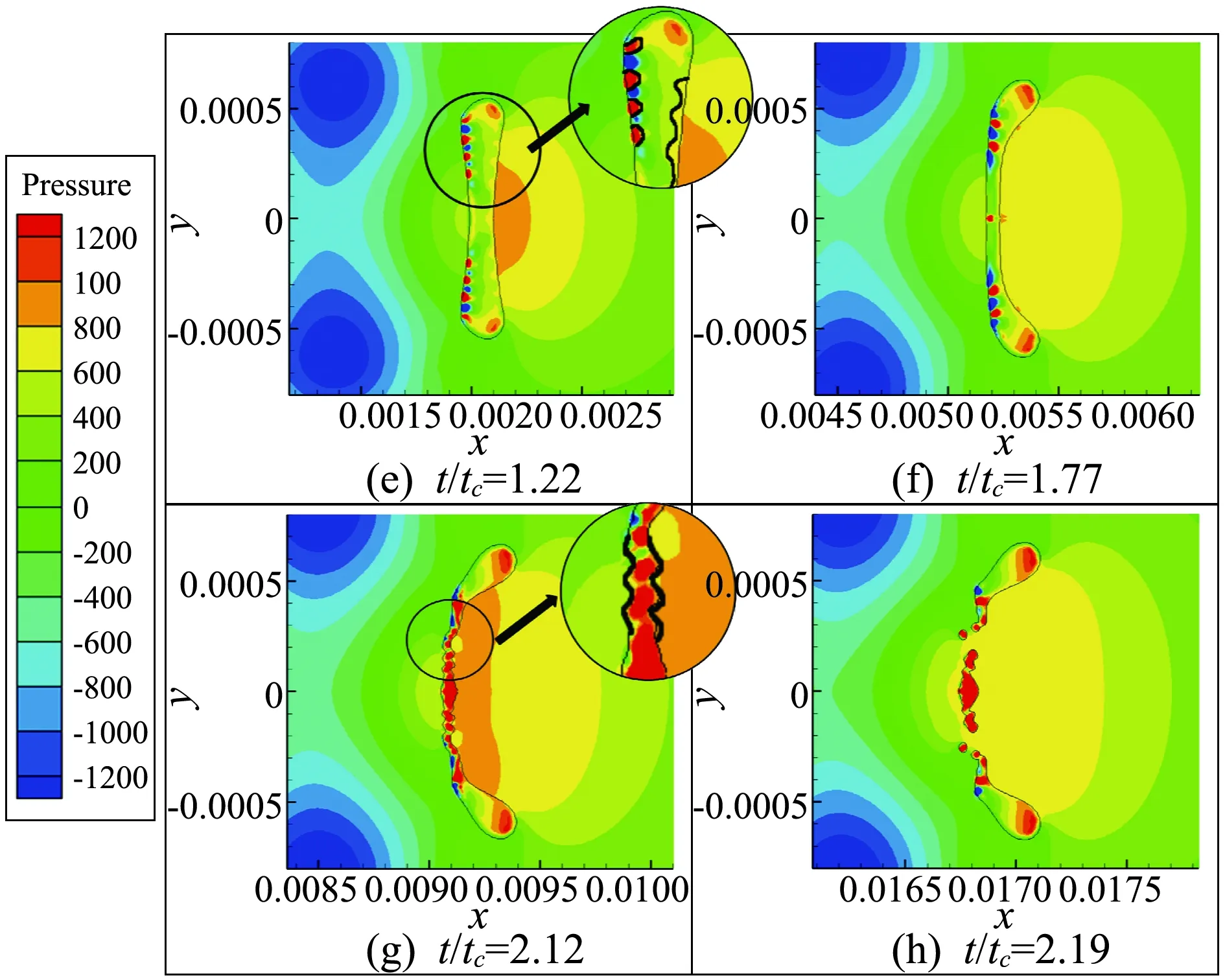
图3 We=16水滴袋装破碎压力云图(水滴运动方向从左至右)(tc =452 μs)Fig.3 The pressure nephogram of water drop (We=16) during bag breakup(tc =452 μs)
2.2 大水滴典型袋状破碎瞬态参数分析
2.2.1 水滴形变及破碎时间分析
水滴袋状破碎过程中的形变和破碎所需的时间是值得关注的重要参数。在前人的工作中,Gordon[16]建立了简易的圆柱体水滴模型用于预测水滴破碎时间,模型假设液体为刚性,气动力将水滴从柱体空间内推出即为水滴破碎;此后又有Rourke&Amsden提出基于弹簧振子系统的TAB模型[17];本课题组创立了将变形过程等效为椭球形水滴的BTB模型[14],认为在变形过程中,当半个水滴的质心在直径方向上发生一定的相对位移后破碎。BTB模型引入修正系数Cm,将相对变形量D=d/d0表示成We数的函数,如式(11)所示。
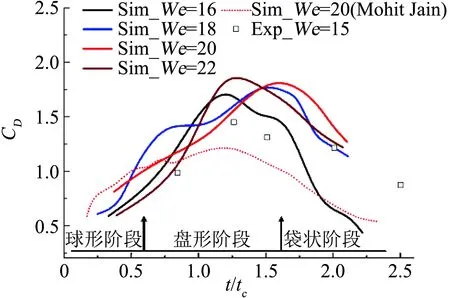
(D-1+D5-2D-4)=80CmWe(0 本文对袋状破碎进行仿真研究,并且将仿真结果与基于BTB模型的计算结果和前人的实验结果[3-4,18]进行比对,如图4所示。其中包括来自Krzeczkowski(We=13.5)、Chou &Faeth (We=15)和Mohit Jain(We=20)。图4中给出了不同We数下袋状破碎水滴随着时间形变的曲线(实验为系列点),并以箭头标出了相应的水滴破碎点。其中y轴坐标为水滴无量纲形变量,即水滴迎风直径d与初始直径d0的比值(在水滴破碎后,迎风直径视为水环的外径);x轴坐标为无量纲时间,即实际时间t与特征时间tc之比。图中水滴We数为16~22,Oh均小于0.005。 图4 水滴相对变形量d/d0与无量纲时间t/tc曲线图Fig.4 Drop cross-stream diameter as a function of time during bag breakup 首先需要明确的是,水滴破碎变形过程主要受到以下几种力的作用:气动力,表面张力和黏性力。其中气动力是发生变形的主因,表面张力和水滴内部的黏性力是减缓和阻止水滴变形的作用力。式(5)中给出的常用参数正是对这三个作用力进行了无量纲化:We数代表气动力比表面张力,Oh数代表了水滴内部黏性力比表面张力。在本文关注的袋状破碎大水滴领域,水滴Oh数远小于0.01,We>10,即黏性力远小于水滴表面张力的量级,而气动力又远大于表面张力,即在水滴运动的短暂时间间隔内动量来不及传递,这意味着水滴将先变形而不是改变速度。因此本文分析的重点放在了气动力和水滴形变上,兼顾表面张力的影响。 由图中三组曲线(仿真组、实验组和拟合组)可以看出,在每组中曲线中,随着We数的增加,水滴的相对变形量也不断增大。此外,在仿真组和实验组的曲线中可以观察到,水滴破碎后曲线斜率明显增大,即水滴残余的水环迅速扩大。联系图3(g,h)的压力云图可以分析得出,水滴袋状薄膜向后凹陷处,存在一个迎风驻点处的高压区,而水滴边缘处由于气流速度增大而静压减小,导致液滴破碎后外侧水环在y方向受力,有一个侧向的加速度,快速膨胀。但随着水滴的破碎,这个压差迅速消失,水环保持一个匀速的膨胀速度直到破碎。本文之所以关注此处水环的变化,是因为在其破碎后形成的水滴虽然数量较少,但却是子水滴群中体积分数最大的部分,在子水滴群中占统治地位。 对于水滴袋状破碎过程中的变形,在Chou和Faeth的实验文献中,不仅给出了实验数据,还提出了相关的经验公式,指出在水滴变形初期过程,相对变形量与无量纲时间呈线性正相关,此后为二次函数关系,具体公式如式(12)所示: 在对本文仿真数据进行拟合后,发现在We=16的条件下,结果与经验公式吻合很好,如式(13),且线性段相关系数R2=0.995: 但随着We数的增长,线性段曲线斜率增大,逐渐偏离经验公式,分析数据后认为这一经验公式更适用于We较低(We=16)的袋装破碎。并且从图中数组曲线可以看出,对于相对形变仿真的结果在全范围内都与试验数据吻合较好;而BTB模型主要关注的是水滴在袋状薄膜临界破碎时期变形量和破碎时间,因此在破碎后期与实验数据贴合更好。 在水滴破碎时间的预测上,BTB模型效果很好:虽然比起实验结果略微偏大,但最大相对误差小于15%,并且在We=20的条件下与实验结果(图5)极为贴近。而仿真数据则普遍偏小,对这一结果进行分析,可以参照水滴破碎试验结果。考虑到实际实验中水滴临界破碎时,不断拉伸的袋状薄膜厚度不断减小,曲率半径随之减小,表面张力不断增加,与气动力达到平衡,保持形态的稳定不发生破碎。直到变形过程中,液膜曲率半径与水环半径一致不再变化,气动力的扰动克服了表面张力,薄膜才发生破碎。但在仿真中,所使用的网格步长为10 μm,大于了临界破碎的水膜厚度,在计算中无法实现水膜的急剧变薄的过程,导致较之实验过早地发生了破碎。对此应做的改进是结合计算经济性,在运算中使用自适应网格,在薄膜处进一步细化网格,才能更好地表现出水膜破碎的完整形态。 图5 水滴在We=20条件下的袋状破碎试验照片[18](气流方向从右至左, tc=110 μs)Fig.5 Experimental observations[18] for We=20(tc=110 μs) 此外从水滴破碎点中可以看出,随着We数的增长,三组数据都显示出一致的趋势:水滴破碎的时间减小,而临界破碎的相对变形量明显增加。 2.2.2 水滴速度与阻力系数 在研究袋状破碎过程中大水滴的速度和受力时,常常要考虑形变带来的影响。显而易见,随着水滴在不同阶段中形状的改变和迎风直径的增大,受到的阻力比起初始球形有着明显的增大,在对阻力和速度进行分析时,常常会引入阻力系数CD,将形变与受力以经验系数的形式联系起来,CD的表达式如式(14)所示,其中u是水滴质心的瞬时速度,a是计算得到的加速度。 图6给出了不同条件下水滴主体无量纲速度变化量(u0-u)/u0和无量纲时间t/tc的关系,以及阻力系数CD曲线。其中除本文仿真结果外,还对照Chou和Faeth[4]的实验结果(We=15)以及Jain[18]的三维数值实验结果,验证仿真正确性。 (a) (b) 从图6(a)中可以观察到,液滴质心无量纲速度在运动初期和末期变化平缓,在t/tc=0.6~1.7之间,发生较为剧烈的变化,即在水滴呈盘形的阶段,速度的相对改变量约为7%。如图6(b)所示,阻力系数CD随着水滴的扁平化,也就是水滴迎风直径的增长而不断增大,并且在迎风直径最大时达到峰值(CD~1.8),此后随着袋状薄膜开始形成,迎风直径不再显著变化,而水滴的背风面形成了光滑的过渡,水滴前后压差减小,CD显著降低。 此外,在起始阶段球形液滴的阻力系数约为0.58,与理论值和实验数据吻合较好。但在峰值处,根据Chou & Faeth[4]的阻力系数拟合曲线,袋状破碎的阻力系数最大值约为1.6,而仿真的结果(CD,max~1.8)比起实验结果偏大,但与不可压缩流(Re<2000)中盘形的阻力系数理论值1.7相近[24]。 本文应用VOF方法,对大水滴典型袋状破碎过程中的特性进行了探究,得到的主要结论如下: 1) 袋状破碎分为五个特征阶段:梯形变形阶段、延伸发展阶段、水环形成阶段、袋状破碎阶段和子液滴形成阶段; 2) 水膜的破碎可以用R-T不稳定性来解释,子液滴的粒径可以应用R-P不稳定性进行预测; 3) 水滴破碎后残余的水环迅速扩大。这是由于水滴袋状薄膜凹陷处,即迎风驻点处存在一个高压区,水环在y向受力导致的; 4) 水滴变形初期过程,相对变形量与无量纲时间呈线性正相关,此后为二次函数关系的关系式,与经验公式吻合很好; 5) 水滴破碎时间随着We数的增长减小,而临界破碎的相对变形量明显增加。 6) 阻力系数CD随着水滴迎风直径的增长而不断增大,最大值约为1.8,此后显著降低。
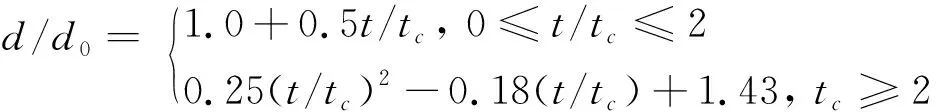
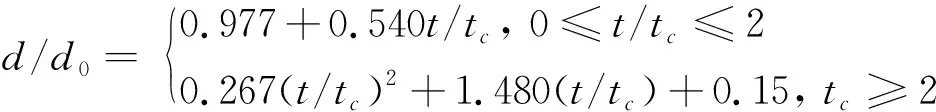

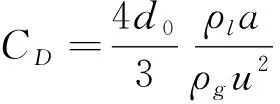

3 结 论

