火星探测器气动热环境和气动力特性的数值模拟研究

刘庆宗, 董维中, 丁明松, 江 涛, 高铁锁

(中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000)

0 引 言

火星是地球轨道外第一近邻，各项自然条件与地球较为接近，是行星探测的首选目标。早在20世纪60年代初，前苏联和美国就逐步开始了火星探测活动。前苏联的火星探测任务大多失败了，美国也只有7次成功着陆火星[1-2]，火星探测充满了困难和挑战。近年来，火星探测又掀起了新的高潮，美国、欧空局、俄罗斯、日本、印度等国都制定了相应的计划，如Scout计划、ExoMars计划、样本返回(MSR)计划等[3-5]。越来越频繁的火星探测计划需要我们对火星大气环境有着更深刻的认识。

火星大气主要由95.7%的CO2、2.7%的N2和少量的Ar等其他组分组成。CO2是三原子分子，具有多个振动模态，且CO2第一振动能级很低，热力学模型比地球大气的更复杂；CO2在较低温度下就容易离解，高温下与N2等气体发生离解、复合、电离等复杂的化学反应，化学特性十分活跃；火星大气十分稀薄，大气压力与密度很低，会导致非平衡松弛时间增大。因此，与地球再入相比，火星大气环境下的热化学非平衡效应十分严重，给准确预测探测器进入火星大气过程中的气动热环境和气动力特性提出了挑战，需要建立合理可信的热化学非平衡模型和计算方法。

20世纪60年代，McKenzie等[6]首先研究了高温CO2-N2混合气体的化学反应体系。90年代，Park等[7]综述了激波加热条件下带电离的CO2-N2-Ar混合气体的非平衡化学反应模型，将激波管数据和燃烧学原理综合起来，给出了适用于火星高超声速进入问题的化学动力学机理。20世纪70年代，Evans等[8]通过求解无黏流加边界层的方法计算Viking绕流流场。90年代，Candler[9]通过求解包含McKenzie化学反应模型和两温度热力学模型的轴对称NS方程，初步研究了火星探测器的热化学非平衡流场。Chen等[10]研究了化学模型、表面催化、输运参数等对火星探测器热表面热流的影响。Mitcheltree等[11]将LAURA程序应用到火星大气的计算中，研究了MPF的表面加热和烧蚀问题。Papadopoulos等[12]对火星大气进入数值模拟CFD程序GASP、GIANTS和LAURA就数值方法、物理化学模型、计算结果等方面进行了详细的说明与对比讨论。目前，美国已经有了成熟的非平衡流场计算程序，能够考虑热力学非平衡、复杂化学反应、表面催化模型以及湍流转捩等一些复杂问题，如GASP、LAURA、DPLR等[12-14]，并与风洞试验数据进行了大量对比验证[15-18]，且在火星探测器Phoenix和MSL上得到应用。

国内火星探测研究还处在起步阶段，数值模拟大多采用简化的完全气体等效比热比方法，也有研究中采用了非平衡方法。杨肖峰、唐伟等[19]基于正激波假设选取完全气体等效比热比，对MSL高超声速流场和气动特性进行了分析。吕俊明、苗文博、程晓丽等[20-23]采用非平衡模型，对火星探测器的气动力/热特性进行了研究。十几年前，作者团队的董维中等对含CO2的热化学非平衡流场进行了数值研究，但主要用于地球再入碳基烧蚀或者混合气体高温辐射计算[24-27]；近年来，丁明松等对国内外火星探测方面的研究进行广泛调研，开展了对火星探测器的绕流流场和气动特性的数值模拟工作[28]。

本文在以前的工作基础上，采用纯CO2化学反应体系以及包含CO2-N2混合气体的化学反应体系，考虑CO2多振动能级的热力学一温度以及两温度模型，耦合表面温度计算方法，建立了完善的数值模拟探测器进入火星大气的热化学非平衡流场计算方法，并与国外平头圆柱试验结果以及MESUR火星探测器计算结果进行对比分析，验证了物理化学模型与计算方法的可行性和可信度，同时针对典型火星探测器，开展了气动热环境和气动力特性的数值模拟研究。

1 数值计算方法

对于高温火星大气非平衡气体模型，比较成熟和实用的热力学非平衡模型是一温度模型和两温度模型，控制方程是三维热化学非平衡Navier-Stokes方程，无量纲化形式如下[29]：

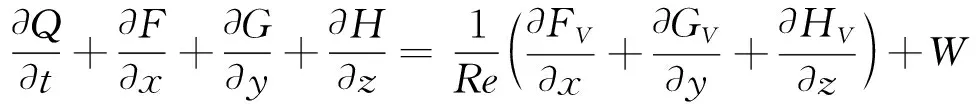
其中，对两温度模型，

Q=(ρi,ρEV,ρ,ρu,ρv,ρw,ρE)T，

W=(wi,wV,0,0,0,0,0)T，

对一温度模型，

Q=(ρi,ρ,ρu,ρv,ρw,ρE)T，

W=(wi,0,0,0,0,0)T。

ρi是组分i的密度，u、v、w为直角坐标系下的速度，E为总能，EV为分子组分的总振动能，Re是雷诺数，F、G、H与FV、GV、HV分别对应不同方向的对流项与黏性项，W为非平衡源项，wi是组分i的化学非平衡源项，wV是振动非平衡源项。

方程(1)中对流项采用AUSMPW+格式离散，黏性项采用中心差分格式离散，时间推进采用全隐式LU-SGS方法，非平衡源项采用隐式处理。

2 物理化学模型

2.1 化学反应模型

国外使用较多的化学反应模型有McKenzie模型[6]和Park模型[7]，这两种模型的组分和化学反应方程式有一定区别，化学反应速率和碰撞效率差别很大。McKenzie模型包含了13种组分19个反应，Park模型包含了18种组分35个反应。Candler、Chen、Mitcheltree等[9-11]为了简化计算，均采用了8组分模型；在纯CO2风洞试验条件计算中，一般采用5组分模型[33]。典型的8组分模型化学反应方程式见表1。化学生成源项计算参考文献[29-30]。

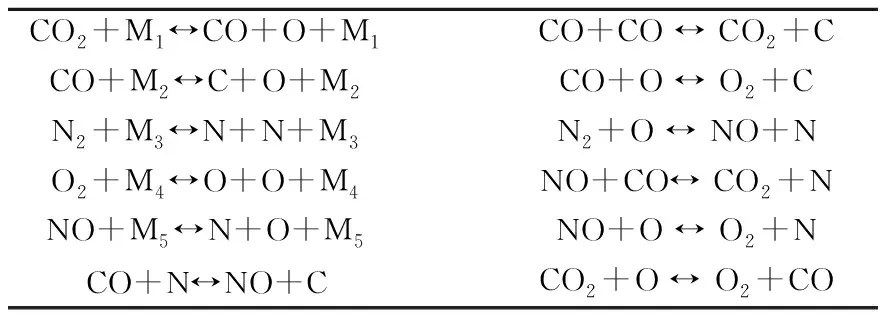
表1 火星大气高温化学反应模型Table 1 Chemical reaction model

2.2 热力学模型

在热力学一温度模型中，假设表征平动、转动、分子振动激发以及电子激发的温度是相等的，只用一个温度T来描述；在热力学两温度模型中，假设分子振动能与平转动能不平衡，分别用平转动温度T和振动温度TV来描述。能量关系式见文献[29-31]。

CO2分子振动能为各振动模态能量之和：

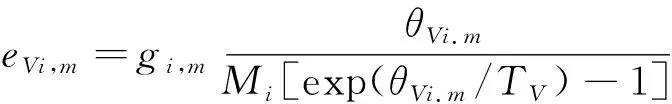
这里θVi.m和gi,m分别是组分i第m个振动模态的振动特征温度和简并度，nmod是振动模态总数，Mi是组分i的分子量。各分子组分振动特征温度和简并度如表2所示。

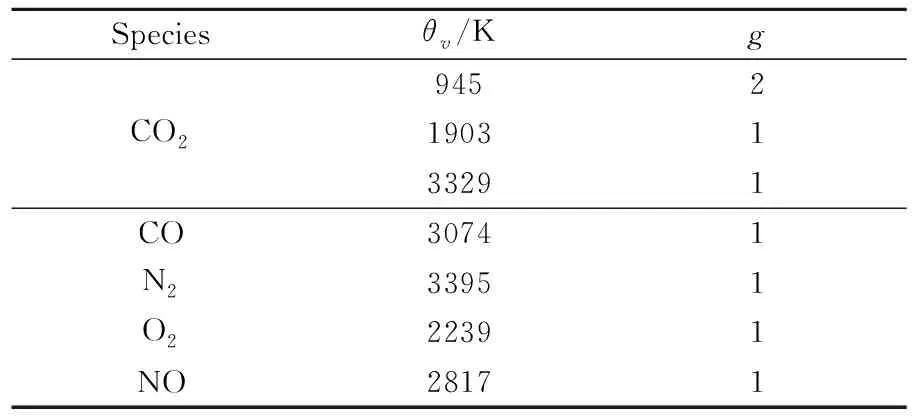
表2 高温火星大气分子组分振动特征温度和简并度Table 2 Vibrational characteristic temperature and degeneracy

振动非平衡源项一般考虑非平衡振动能与平衡振动能之间的松弛过程以及非平衡源项的生成：

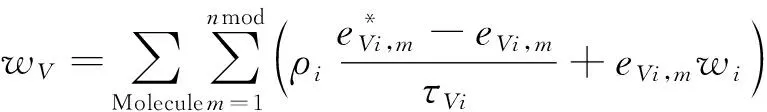
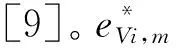
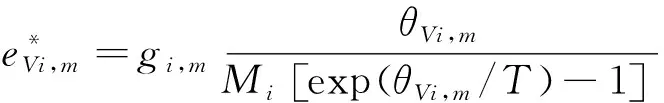
2.3 表面计算模型

表面材料的催化特性一般按完全非催化条件(NCW)和完全催化条件(FCW)两种方法处理。

表面温度条件通常采用等温壁条件，但实际情况中，飞行条件对探测器表面温度影响较大，且不同部位的表面温度差别较大，会给精确预测探测器气动热环境和气动力特性带来一定偏差，可进一步考虑表面辐射效应和催化效应，使用辐射平衡表面温度分布条件[34]：

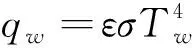
其中qw是飞行器表面热流，ε是表面材料辐射系数，σ是斯特藩-波尔兹曼常数。

3 计算方法验证

3.1 平头圆柱试验模型

为验证物理化学模型和计算方法的正确性，首先选取带有试验和计算数据的平头圆柱算例[35]。试验模型尺寸如图1所示，试验条件见表3。化学反应采用5组分Park模型，热力学模型采用一温度模型，等温壁Tw=300 K，表面催化分别采用NCW和FCW条件。该算例主要考核激波位置、压力以及表面热流分布。

图1 平头圆柱实验模型尺寸Fig.1 Schematic of test model

表3 平头圆柱试验模型计算状态Table 3 Test conditon of blunt cylindrical model

图2为FCW条件下流场温度云图，激波位置和流场结构十分清晰。图3为驻点线组分分布与文献对比，图4和图5为表面压力、热流与文献和试验结果的对比。可以看出：本文计算的流场组分、压力与文献和试验结果一致；表面催化条件对热流影响较大，FCW热流明显比NCW热流高，试验得到的热流几乎处于两者之间，接近于完全催化结果。总的来说，计算结果与文献和试验结果一致，物理化学模型和计算方法的正确性得到验证。

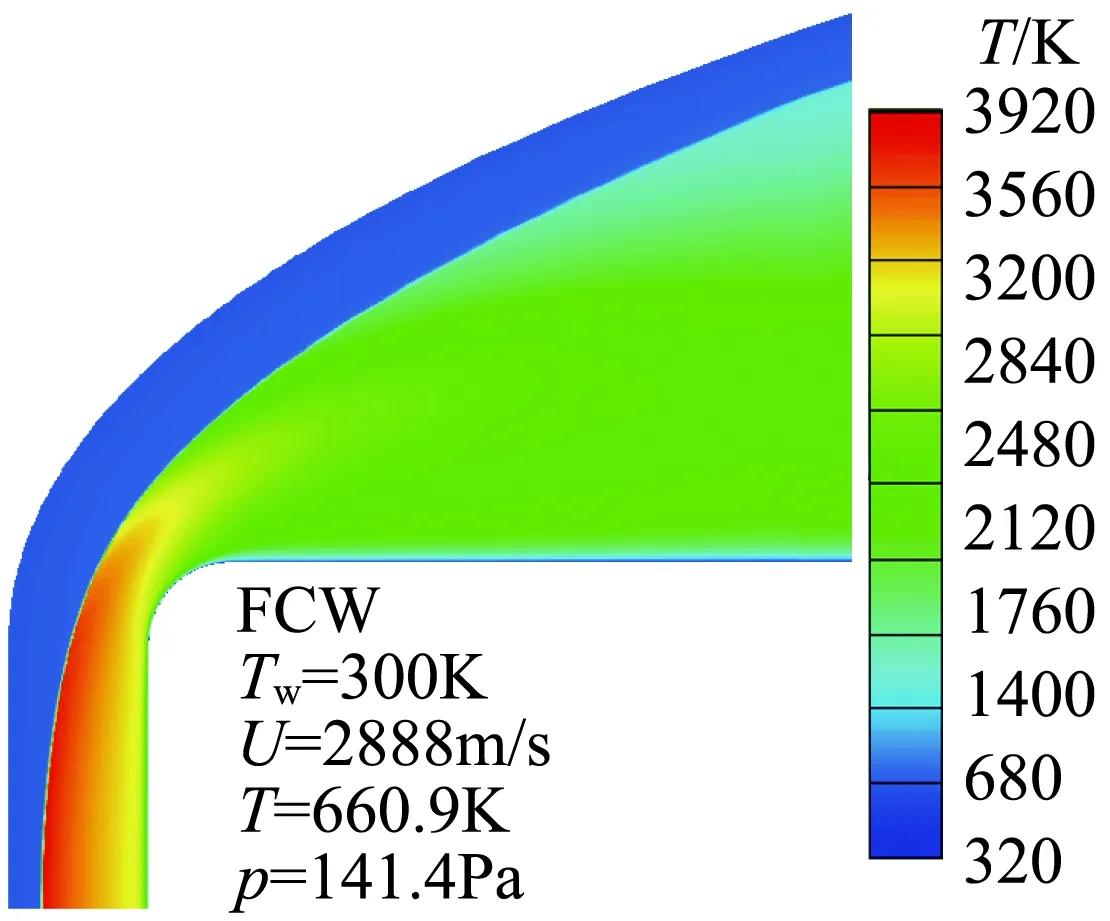
图2 平头圆柱流场温度云图(FCW)Fig.2 Temperature contours

(a) NCW

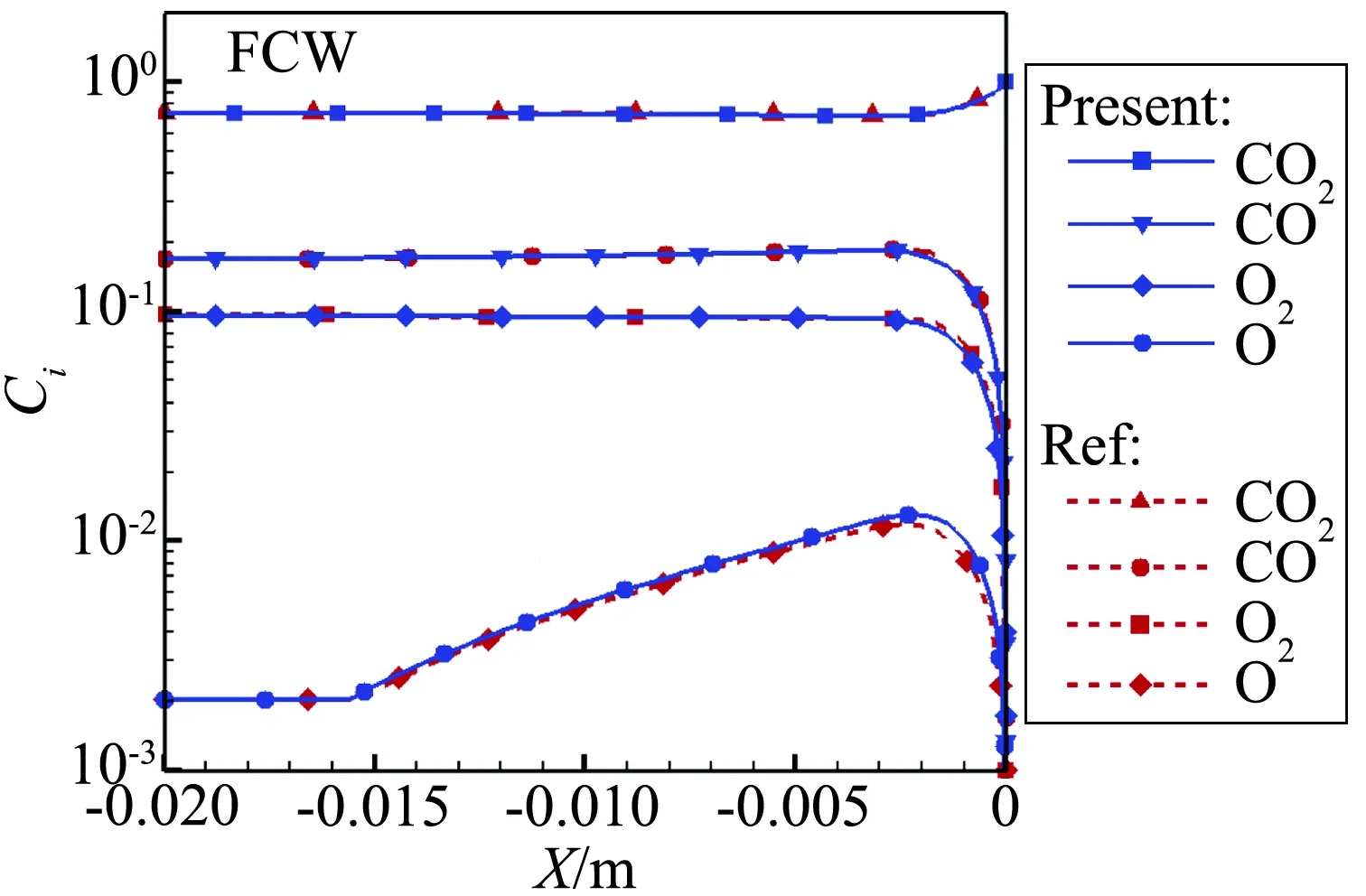
(b) FCW

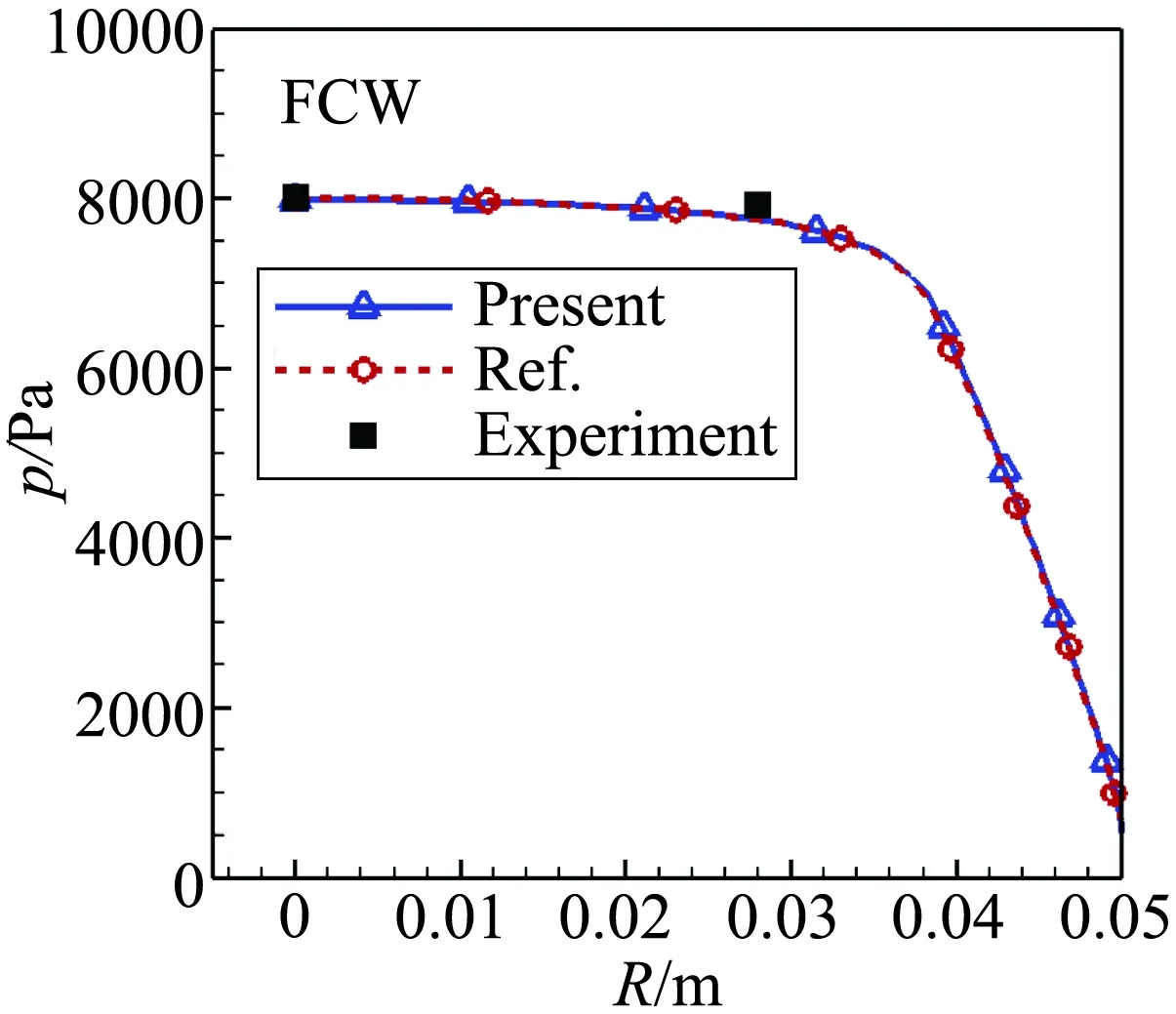
图4 平头圆柱表面压力与文献和试验对比(FCW)Fig.4 Surface pressure (FCW)

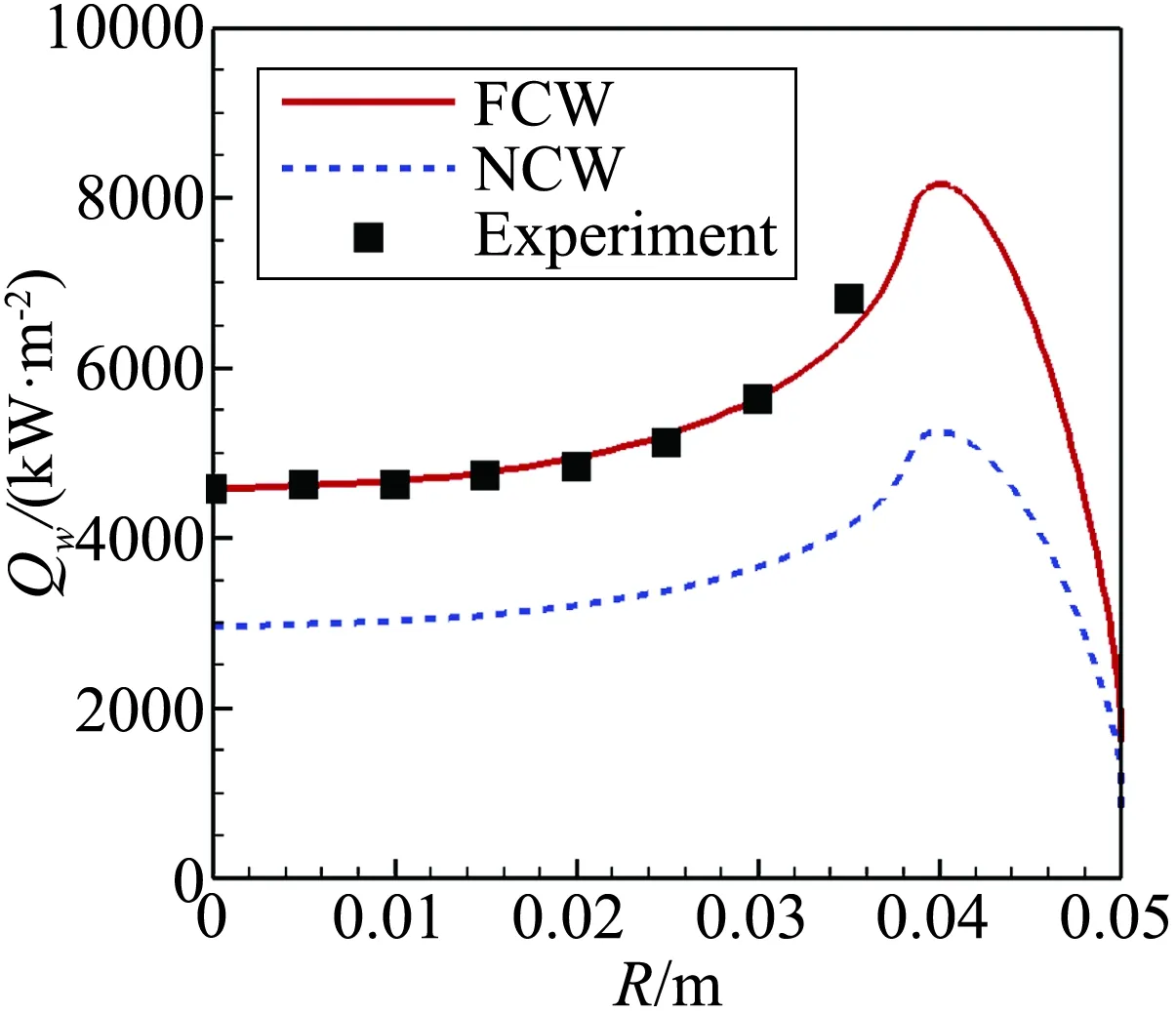
图5 平头圆柱表面热流与试验对比Fig.5 Surface heating rates

3.2 MESUR大底模型

为进一步验证物理化学模型和计算方法适用于火星探测器外形计算，并考核辐射平衡表面温度模型的有效性，选取了MESUR大底外形算例[10]。计算状态见表4，化学反应采用8组分Park模型，热力学模型采用两温度模型，壁温采用辐射平衡条件。

表4 MESUR探测器计算状态Table 4 Computational condition of MESUR probe

图6为两温度模型下流场CO2分布云图，流场中CO2大部分区域离解程度在90%以上，化学反应非常剧烈。图7和图8为表面温度和热流计算结果与文献对比，总体上本文结果与文献结果吻合得很好，表面热流偏差在5%以内，表面温度偏差在1%左右，说明本文建立的物理化学模型和计算方法适用于典型火星探测器外形的气动热计算，辐射平衡表面温度模型的正确性也得到验证。

图6 MESUR流场CO2分布云图Fig.6 Mass fraction of CO2

图7 MESUR表面温度分布与文献对比Fig.7 Surface temperature

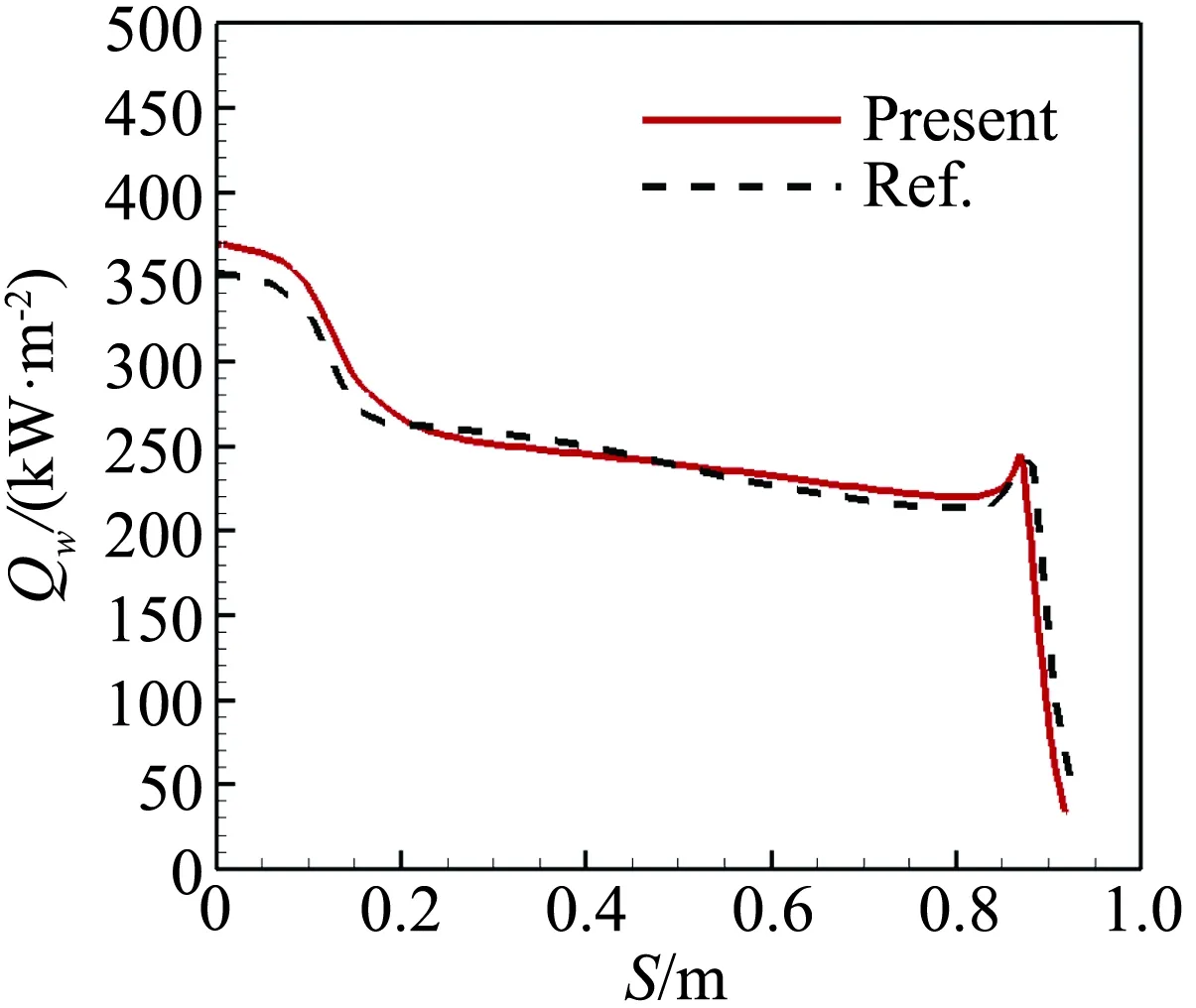
图8 MESUR表面热流分布与文献对比Fig.8 Surface heating rates

4 气动热环境计算分析

为分析化学反应模型、热力学模型、表面催化特性和迎角等因素对探测器气动热环境的影响和变化规律，对典型外形火星探测器进行了数值模拟。计算状态为H=40 km、30 km，速度V=4.2 km/s、3.0 km/s；迎角为0°～30°；壁温Tw=300 K；表面催化分别采用NCW和FCW条件。热力学模型分别采用一温度(1T)和两温度模型(2T)；化学反应采用8组分Park模型，标记为Park，对比时还采用了8组分McKenzie模型，标记为McKenzie。

图9为H=40 km时流场平动温度和CO2分布云图。可以看出，探测器大底前激波较薄，激波后温度很高，大部分在3500 K左右，最高达到7000K以上；流场中CO2组分变化较大，离解程度可达60%以上，热化学反应十分剧烈；离解产生的混合气体随流动向后拓展，将火星探测器包裹在强烈的热化学非平衡反应气流中。

(a) 平动温度

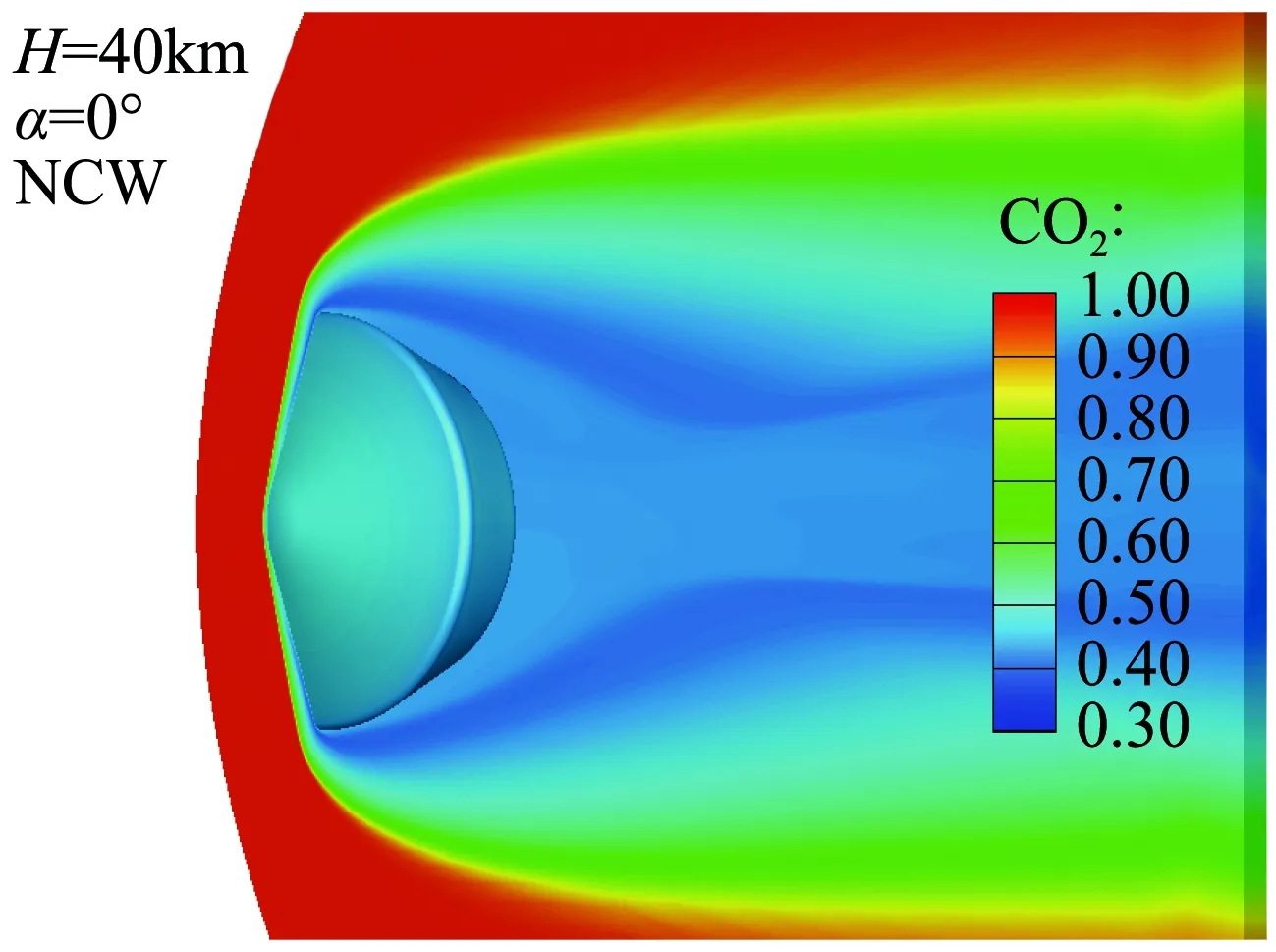
(b) CO2质量分数

图10为H=40 km时两种化学模型得到的表面热流分布。可以看出，两种化学模型的热流分布规律相似，但热流值差别较大；NCW条件下，McKenzie模型的热流比Park模型高出50%～60%，NCW热流结果对化学反应模型比较敏感；FCW条件下，McKenzie模型和Park模型热流结果相差较小，FCW热流结果对化学反应模型不太敏感。说明不同化学反应模型对表面催化效应的敏感程度有差别，化学反应模型对气动热计算影响较大。

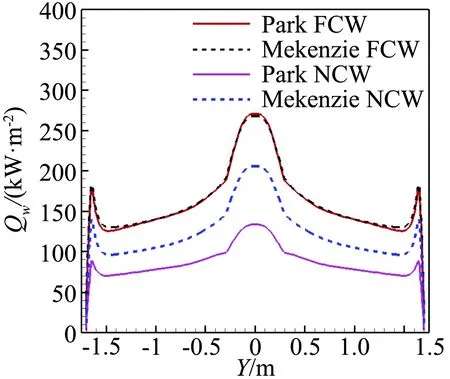
图10 不同化学模型的表面热流结果对比Fig.10 Surface heating rates

图11和图12分别为H=40 km时两种热力学模型得到的头部轴线温度分布和表面热流分布。可以看出，两种模型头部轴线温度有一定差别，存在热力学非平衡现象；两种模型热流分布规律基本一致，热流值有一定差别，FCW条件下一温度模型与两温度模型的热流峰值差别在7%左右，NCW条件下二者差别在3%左右，热力学模型对表面热流的计算有一定影响。

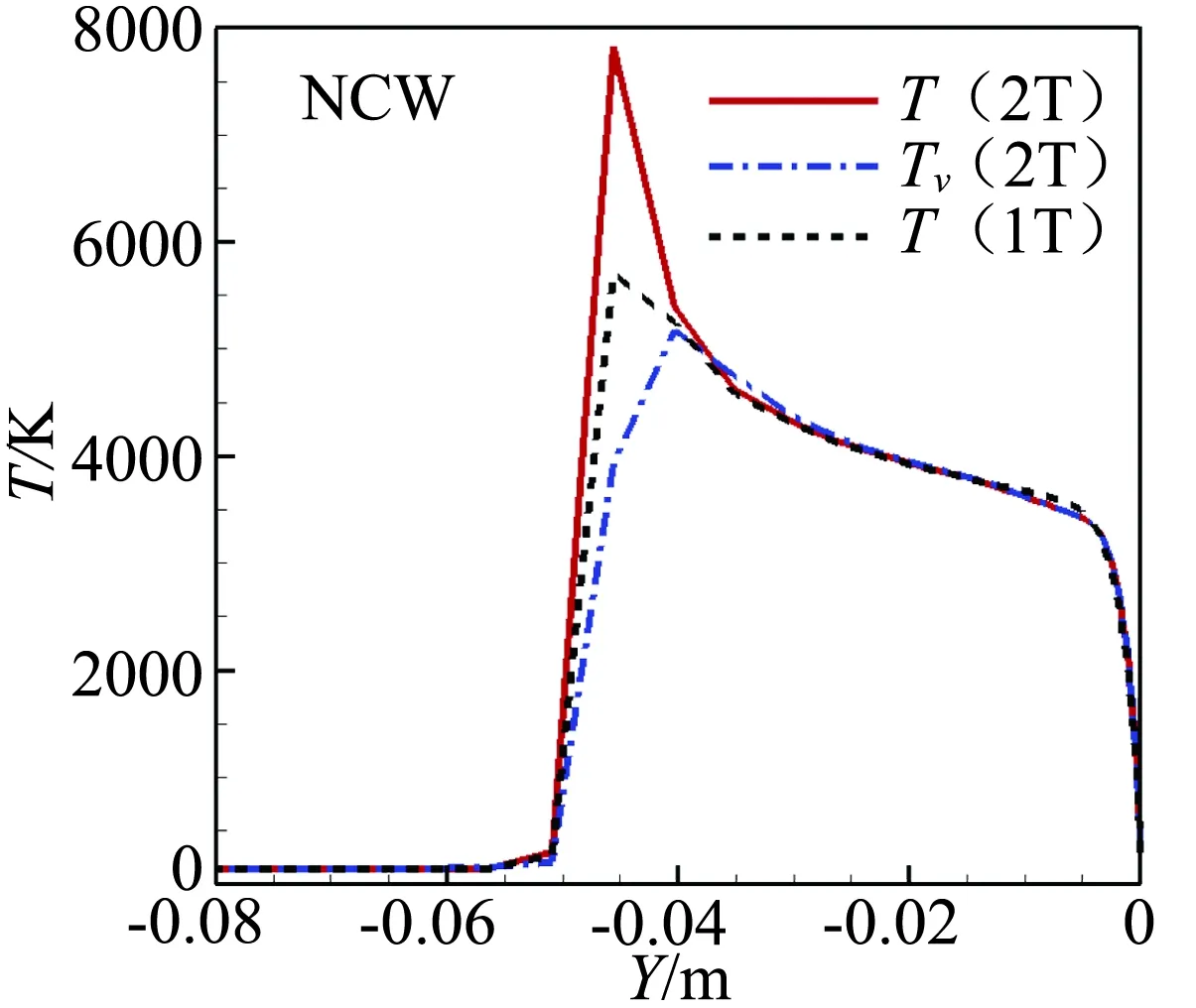
图11 不同热力学模型头部轴线温度对比Fig.11 Temperature along axisymmetric line

图12 不同热力学模型表面热流结果对比Fig.12 Surface heating rates

图13为探测器不同弹道高度表面热流，图14为头部轴线温度和CO组分分布。由图可知，弹道高度高时，飞行速度大，头部附近流场温度高，壁面附近CO组分浓度大大增加，FCW和NCW热流相差变大；在H=40 km时，防热大底区域内的FCW热流达到NCW热流的2倍到2.5倍。说明弹道高度和飞行速度增大时，化学反应增强，催化作用对热流影响增大。

图15为探测器大底顶点附近和迎风肩部附近热流峰值随迎角的变化。可以看出：随着迎角增大，顶点附近热流峰值有减小的趋势，肩部附近热流峰值有增大的趋势；在30°迎角时，肩部附近热流峰值急剧增大，FCW条件下热流达到350 kW/m2左右。

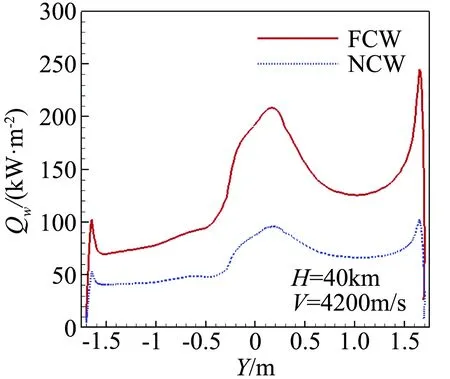
(a) H=40 km

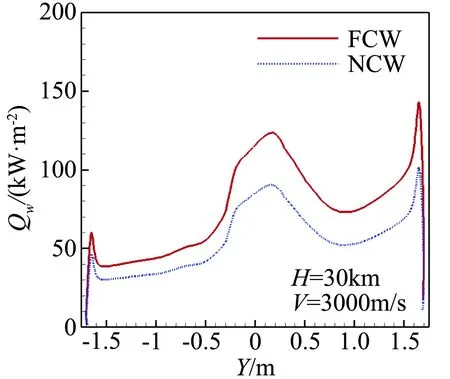
(b) H=30 km

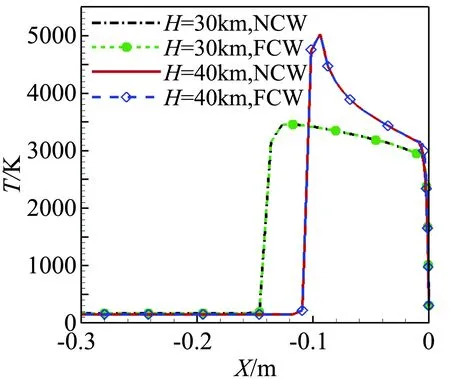
(a) 温度

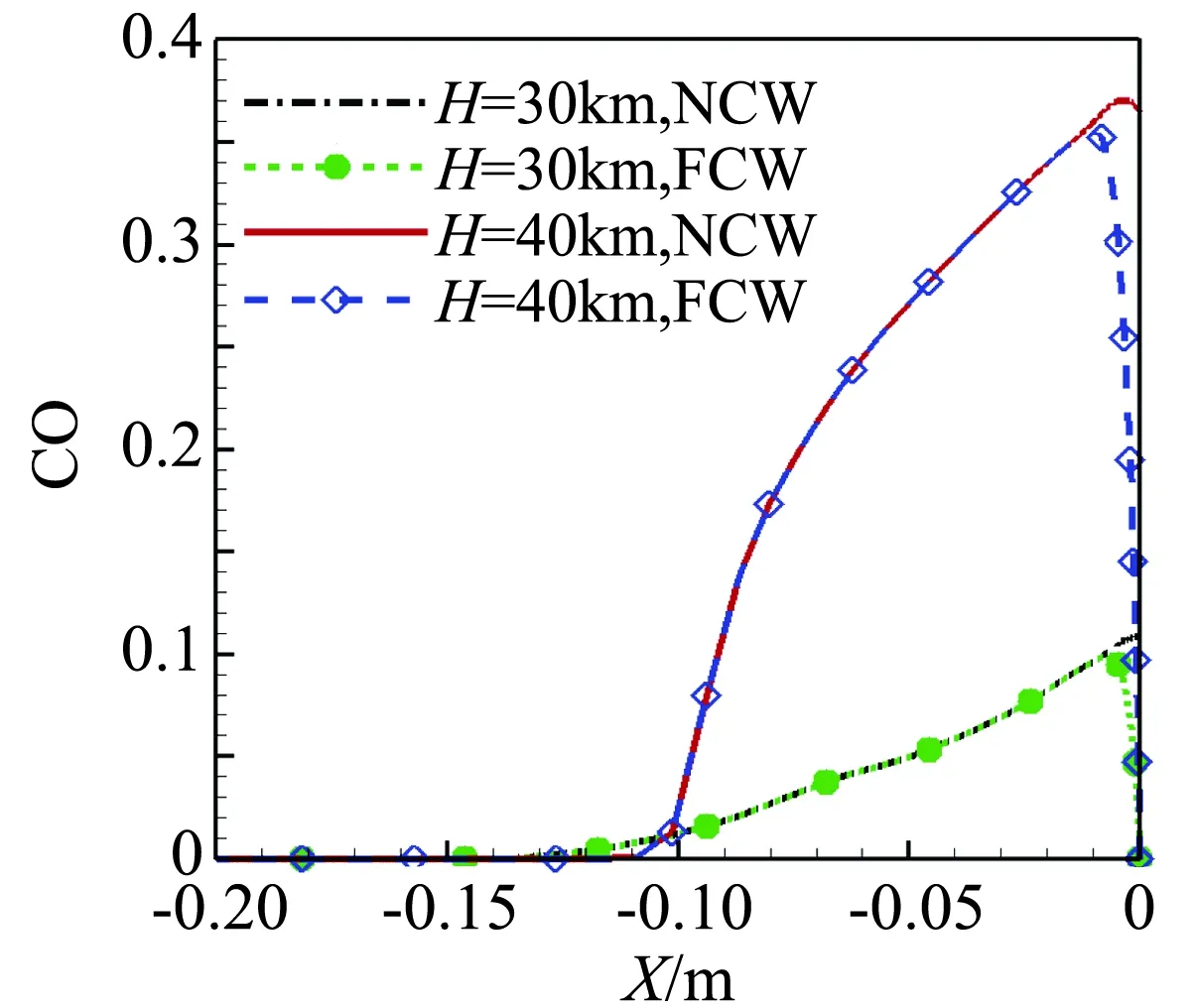
(b) CO

(a) 顶点附近

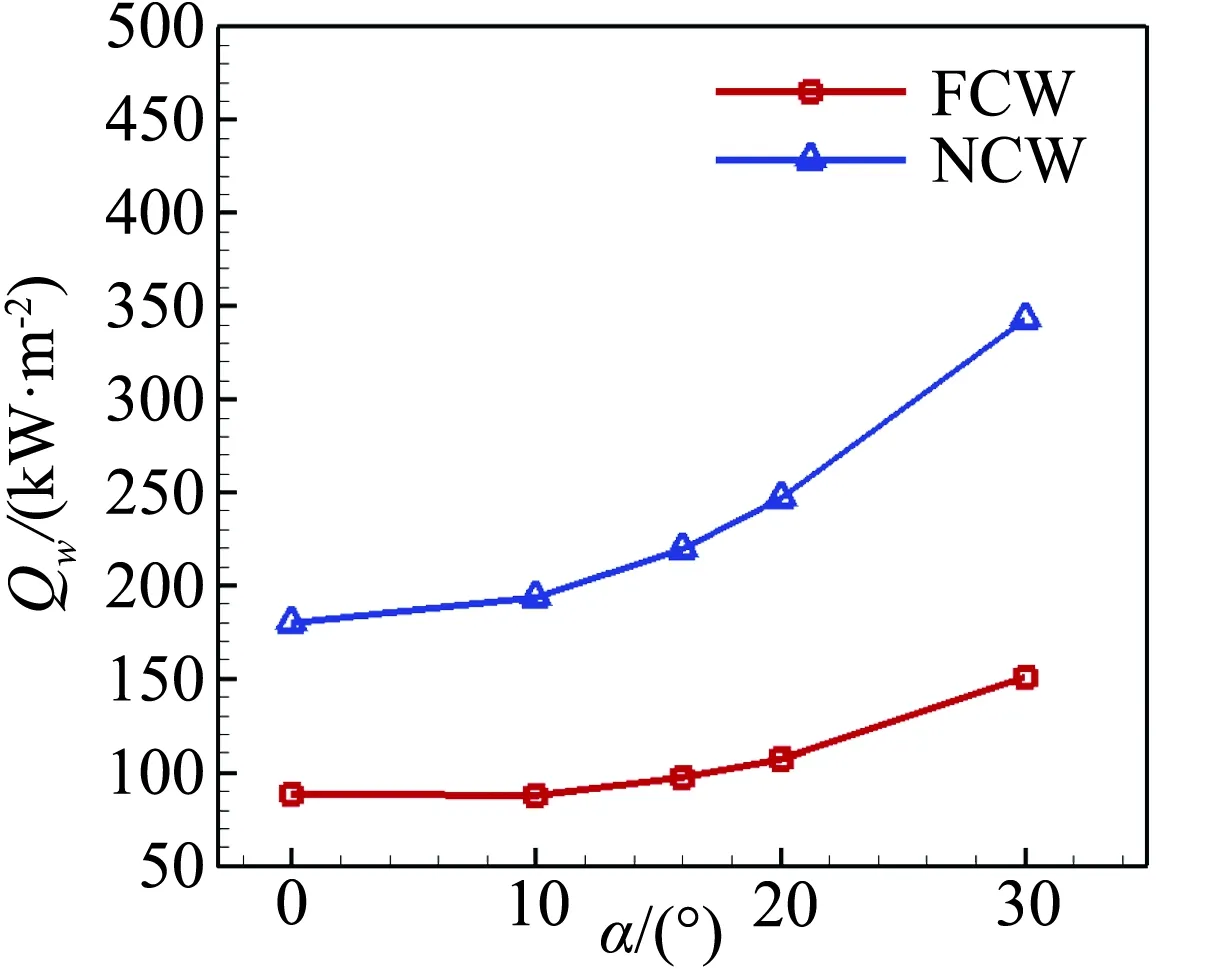
(b) 肩部附近

5 气动力特性计算分析

为研究流场中的非平衡效应对火星探测器气动力特性的影响，采用完全气体模型和非平衡气体模型，对探测器的气动力特性进行了数值计算。在此基础上，进一步分析非平衡气体模型中表面温度条件和表面催化特性对气动力特性的影响。

计算状态为H=41.6 km，V=4650 m/s，迎角为0°、11°、16°和20°。非平衡模型中采用热力学一温度模型和8组分Park化学模型。完全气体模型中，等效比热比分别取为γ=1.1、1.15、1.2、1.3。

图16为一温度非平衡气体模型和不同比热比完全气体模型头部轴线温度及轴向力系数对比。可以看出：与等效比热比较大的完全气体模型相比，非平衡效应使得激波脱体距离和波后温度减小，轴向力显著增大；完全气体模型中，随着等效比热比的减小，激波脱体距离和波后温度逐渐减小，轴向力有明显增大；本文状态的非平衡流场激波脱体距离、波后温度分布以及轴向力系数与完全气体模型γ=1.1比较接近。总的来说，完全气体模型与非平衡气体模型计算的流场和气动力特性有较大差异；完全气体模型计算方法的计算速率十分快，但等效比热比的选取问题是该方法中的一个难点；非平衡气体模型能更真实的模拟探测器流场情况，在精确计算气动力特性时，建议采用非平衡气体模型。

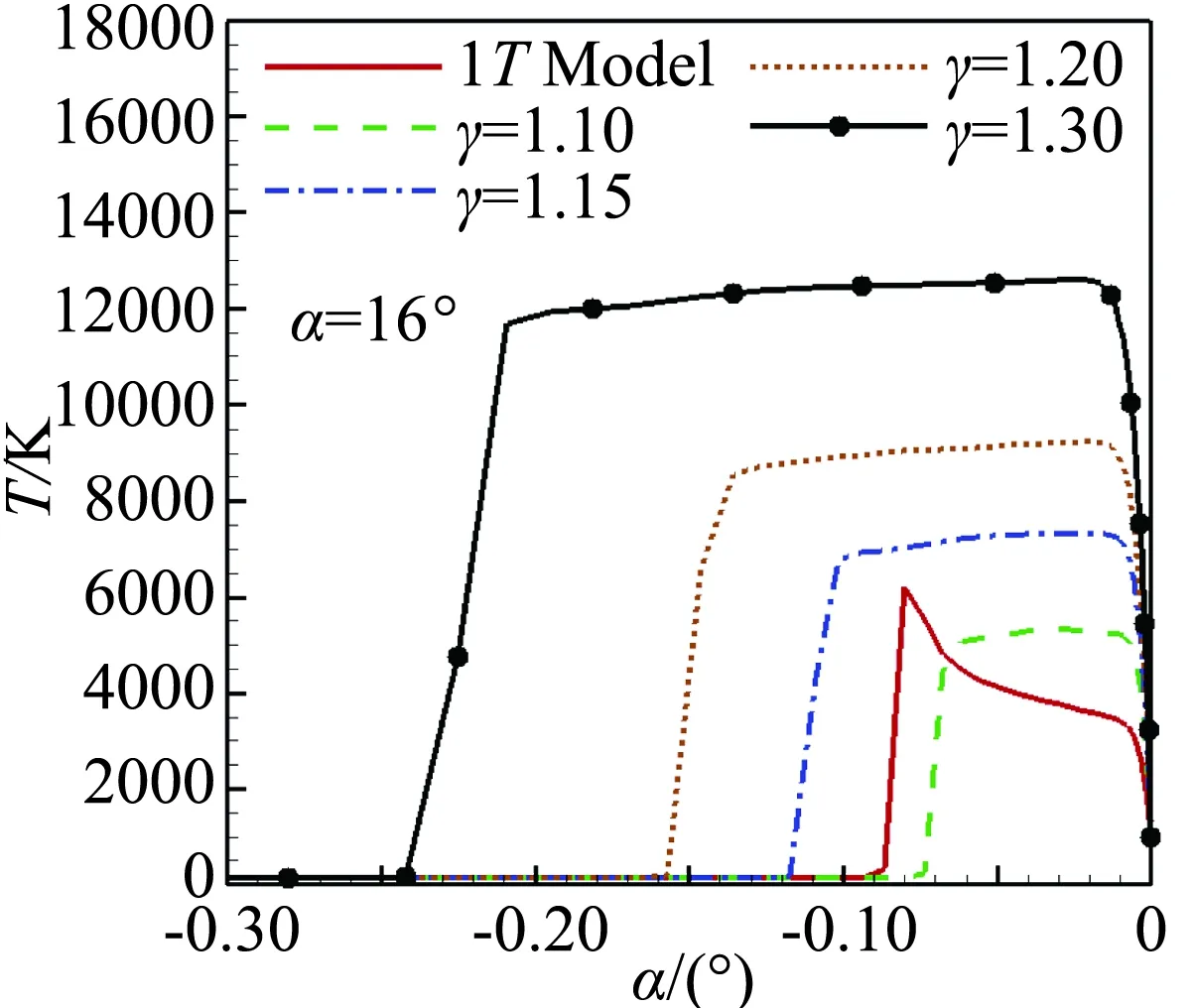
(a) 头部轴线温度分布(α=16°)

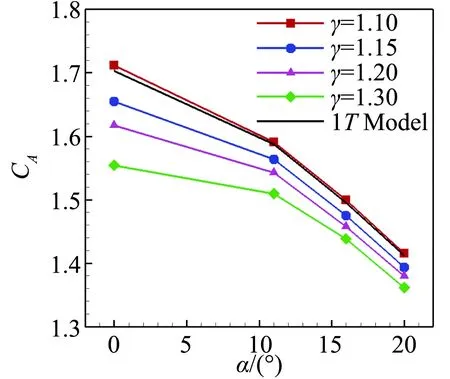
(b) 轴向力系数

图17为不同壁面温度条件下的轴向力系数，图18为不同表面催化条件下的轴向力系数，可以看出，表面温度条件和表面催化特性对气动力系数的影响较小。

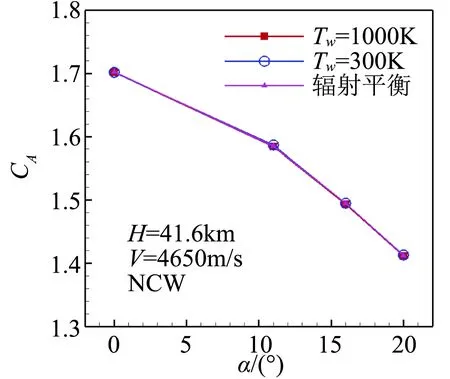
图17 不同表面温度条件下的轴向力系数Fig.17 Axial force coefficients of different wall temperature conditions

图18 不同表面催化条件下的轴向力系数Fig.18 Axial force coefficients of different surface catalytic conditions

6 结束语

通过本文的研究，建立了完善的火星大气高温热化学非平衡流场数值计算方法和程序，该程序可以考虑不同化学反应模型、不同热力学模型(一温度/两温度)、不同表面催化条件(NCW/FCW)以及不同表面温度条件(等温/绝热/辐射平衡)，能够数值计算火星探测器热化学非平衡气动热环境和气动力特性，并采用平头圆柱试验模型和MESUR火星探测器进行了考核验证，计算结果与试验和文献一致，可信度高。采用该方法和程序，针对火星探测器的多个典型飞行状态，开展了非平衡流场气动热环境和气动力特性数值模拟研究，得到以下结论：

1) 对于本文的计算状态情况，火星探测器流场中化学非平衡效应非常严重，存在一定的热力学非平衡效应。在化学非平衡效应非常严重时，流场中CO2离解程度非常高，主要组分是CO2，CO，O2和O；不同气体模型计算的头部激波位置和温度分布差异比较大；一温度和两温度非平衡气体模型计算的温度分布和气动热也有一定的差异。

2) 热力学模型、化学反应模型和表面催化特性对气动热计算都有着重要影响。不同化学反应模型得到的完全非催化热流差别很大，完全催化热流差别较小；热力学模型对气动热计算有一定影响，最大差别在7%左右；表面催化对热流影响很大，完全催化热流达到非催化热流的2倍到2.5倍。精确预测探测器的气动热环境时，建议采用两温度热力学模型，选择合适的化学反应模型，考虑表面催化特性和表面温度分布。

3) 火星探测器防热大底上一般在大底顶点附近和肩部附近会出现热流峰值；随着飞行迎角的增大，顶点附近的热流峰值有减小的趋势，迎风侧肩部附近的热流峰值有增大的趋势。

4) 表面温度条件和表面催化特性对气动力系数的影响较小，完全气体模型与非平衡气体模型计算得到的流场和气动力特性有较大差异。精确预测气动力特性时，完全气体模型存在选择合适等效比热比的难题，建议采用非平衡气体模型。

基于本文建立和完善的火星大气高温热化学非平衡流场数值计算方法和程序，可以进一步开展如下三个方面研究工作：1) 表面有限催化特性研究。本文只研究了完全非催化和完全催化两种情况，探测器表面催化速率一般为有限值，受飞行器表面温度、表面材料种类等多种因素影响，而表面催化强弱又反过来影响表面温度的高低和表面附近气体组分的质量分数，进而影响整个热化学非平衡流动。2) 高空稀薄火星大气热化学非平衡流动研究。本文的计算状态主要是气动热严峻的较低高度，气体密度降低会使热化学非平衡的松弛时间变长，在更高空的火星大气环境中(如H=50 km以上)，火星大气更加稀薄，热力学非平衡效应可能更加严重。3) 考虑多个振动温度的火星大气热力学非平衡流动研究。火星大气主体成分CO2包含多个振动能级，高温下各振动能级激发程度往往不一致，其它火星大气分子(N2、O2、CO、NO等)振动激发程度也各不相同，需要用不同的振动温度来描述。