弯曲和旋转修正的湍流模型在旋转翼身组合弹箭中的应用研究

石 磊, 杨云军, 周伟江

(中国航天空气动力技术研究院, 北京 100074)

0 引 言

高速旋转会产生很强的壁面剪切层[1-2]，湍流剪切应力对流线弯曲和模型旋转很敏感，在凹角区域及旋转管道的抽吸侧，湍流都得到了增强，在凸表面及旋转管道的受压侧，湍流都得到了削弱，传统的基于Boussinesq线性涡黏性假设的湍流模型(如一方程Spalart-Allmaras(SA)模型、两方程k-ωShear-Srtess-Transport(SST)模型、k-epsilon(k-ε)模型)不能准确的捕捉到这种特性[3-4]，因为当模型旋转时，科氏力(Coriolis forces正比于二阶应力分量)以旋转生成项的形式在雷诺应力张量中体现，但是输运方程中应力张量的对角项是相互抵消的，旋转效应体现不明显。雷诺应力方程中可以显含弯曲和旋转效应的生成项，但是其昂贵的计算代价，使得在实际应用中还鲜有见到。对涡黏性模型进行弯曲和旋转效应修正，使其实现或近于实现：1)单纯的旋转运动不引入额外的湍流；2)近壁面的流线弯曲在湍流特性中有体现；3)不增加太多的计算计时；4)能应用到工程问题中，是近半个世纪高速旋转问题研究中众多学者不懈奋斗的方向。

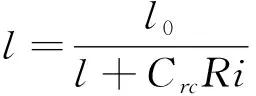
1997年Spalart和Shur[10-11]提出了一种半经验的通用三维修正模型(SARC，RC代表弯曲和旋转修正)，在生成项前引入fr1函数，函数中引入应变率张量拉格朗日导数(Lagrangian Derivative)对湍流中的弯曲和旋转量进行简单模化，为保证伽利略不变性(Galiean-invariant)，求导沿着主应变轴进行。随后对雷诺数Re=11500～36000、滚转数Ro=0.0～0.21管道旋转流动进行了计算，与实验和直接数值模拟(DNS)结果比较后发现壁面速度型、分离区、凹凸区域的摩擦系数都比SA和SST模型有了很大改善，但存在在小滚转数下摩擦速度偏大，大雷诺数下弯曲特性预估不足、再附区偏长等问题。1998年Hellsten[12]通过对三维流动中弯曲和旋转效应敏感的物理量进行分析，在k-ωSST模型中引入弯曲函数F4，同时修正壁面边界的ω值，提出了一种通用修正模型(SSTRC)，并对马赫数Ma=0.2，Re=35000旋转管道流进行了计算，发现Ro小于0.21时与实验符合很好，大滚转数时失效，随后对ONERA-A翼形计算发现与原始的k-ωSST结果相差不大。2004年Mani[13-14]使用Wind代码，对Ma=0.2，Re=3.28×106亚声速U型管算例对比了SARC和SSTRC修正模型，发现在分离区前都与实验结果符合很好，但是分离区出现压力过估、再附区出现摩阻预估不足的问题。2012年Sunil[15]使用FOAM代码，通过模化湍流输运方程中的湮灭项实现对旋转和流线弯曲的控制，并对旋转的槽道、凹曲面的边界层进行了数值模拟，发现比SSTRC模型预测结果略优。2013年Nash[16]使用FUN3D代码，采用SA和SARC模型，对Ma=0.15、Re=4.6×106翼尖涡脱落及向后传播的历程进行了数值模拟，发现SARC模拟的涡核轴向速度和压力与实验结果符合更好。2015年Rumsey[17]使用CFL3D和FUN3D代码，对Ma=0.2，Re=4.2×106、迎角α=6°～37°的NASA梯形翼进行了计算，发现SARC、SSTRC模型预测的升力更大、对翼尖涡及向下游传播的历程刻画更精细，但没有改善翼尖附近的压力分布。

国内对湍流模型中弯曲和旋转效应修正的研究还比较少见，只调研到1997年李卫东[18]采用不同的紊流黏性系数构造了一种修正的k-ε模型，并计算了液-液旋流分离器内锥变截面流场。弯曲和旋转修正的湍流模型在弹箭旋转气动特性方面的研究，国内、外还未见到。为此，本文采用完全时间相关的非定常Navior-Stokes(N-S)方程，以一方程SA湍流模型和两方程SST湍流模型为基础，对典型带翼弹箭开展研究，从气动特性和流场结构分析了SARC及SSTRC修正模型对计算精度的影响。

1 数值方法

1.1 控制方程

积分形式的时间相关三维可压缩N-S方程为：

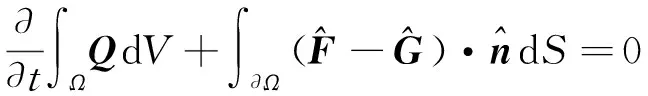
本文计算采用的湍流模型包括SA一方程湍流模型：

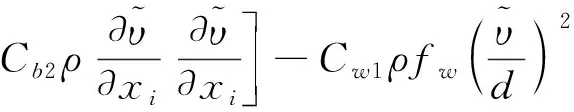
以及k-ωSST两方程湍流模型：

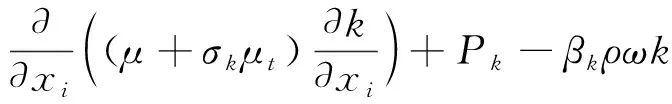
第一种弯曲和旋转修正采用文献[10]中的Spalart发展的SARC方法：

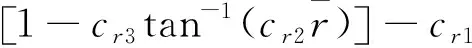
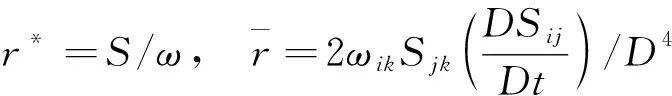
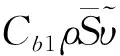
第二种弯曲和旋转修正采用文献[12]中Hellsten发展的SSTRC方法：

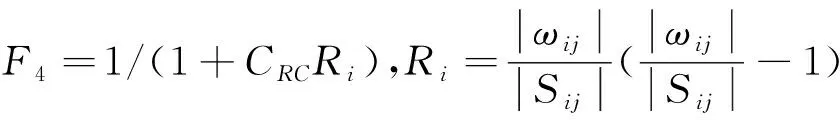
其中，F4为弯曲函数，作用于ω方程中的衰减项ρβωω2来实现对弯曲和旋转效应的修正，Ri下界为-1/4，系数CRC参考文献[12]中取为3.6。

1.2 数值求解方法

求解采用格心格式的结构有限体积法，Roe格式计算无黏通量，反距离权重最小二乘法计算单元梯度，Venkatakrishnan限制器抑制间断附近的过冲和振荡。基于Riemann条件的远场边界条件，Riemann不变量构造时需要计及网格速度；壁面边界条件要求壁面流体速度和网格运动速度相同。非定常计算采用双时间步法，物理时间层采用二阶向后差分离散，伪时间层采用Low Upper Symmetric Gauss-Seidel(LU-SGS)隐式时间推进。

1.3 计算模型及计算网格

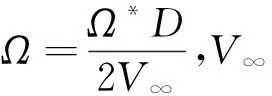
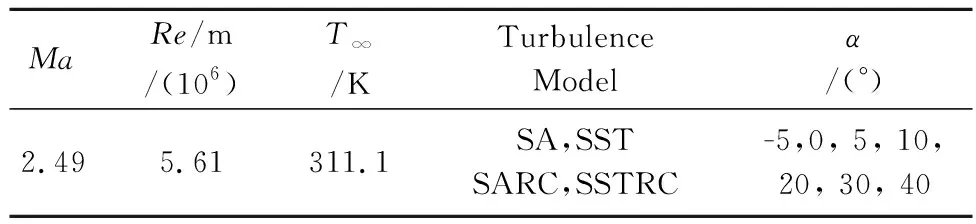
表1 AFF计算条件Table 1 Calculation conditions

本文参考文献[20]的网格分布，生成的计算网格(图1)流向×法向×周向为：250×200×250，网格单元数共1255万，法向第一层网格间距均为5×10-6m，保证壁面y+≤1。

图1 AFF对称面计算网格Fig.1 Computational grids for AFF

1.4 旋转周期和角度定义

图2给出了旋转周期及角度定义，从弹体底部向前看，逆时针旋转为正，周向角θ=0°～90°、270°～360°为背风区，周向角θ=90°～270°为迎风区。沿x、y、z轴分别为轴向力、法向力、侧向力，绕x、y、z轴分别为滚转力矩、侧向力矩、俯仰力矩。可知侧向力系数CZ即为马格努斯力系数，偏航力矩系数CMY即为马格努斯力矩系数。

图2 计算坐标系及角度定义Fig.2 Coordinate system and angle definition

2 计算结果与分析

2.1 马格努斯力和力矩系数数值模拟结果

图3给出了迎角α=-5°～40°动态气动特性随迎角变化规律，并与AEDC实验[19]及美国陆军研究实验室(ARL)计算结果[20]进行了对比。从图中可知侧向力矩旋转导数CMYΩ随迎角增加呈减小趋势，侧向力旋转导数CZΩ随迎角增加先减小后增大，在a=14°附近出现拐点，拐点附近的计算值比实验值略小。总体而言本文计算结果与实验及文献结果吻合很好，验证了数值方法的可靠性。

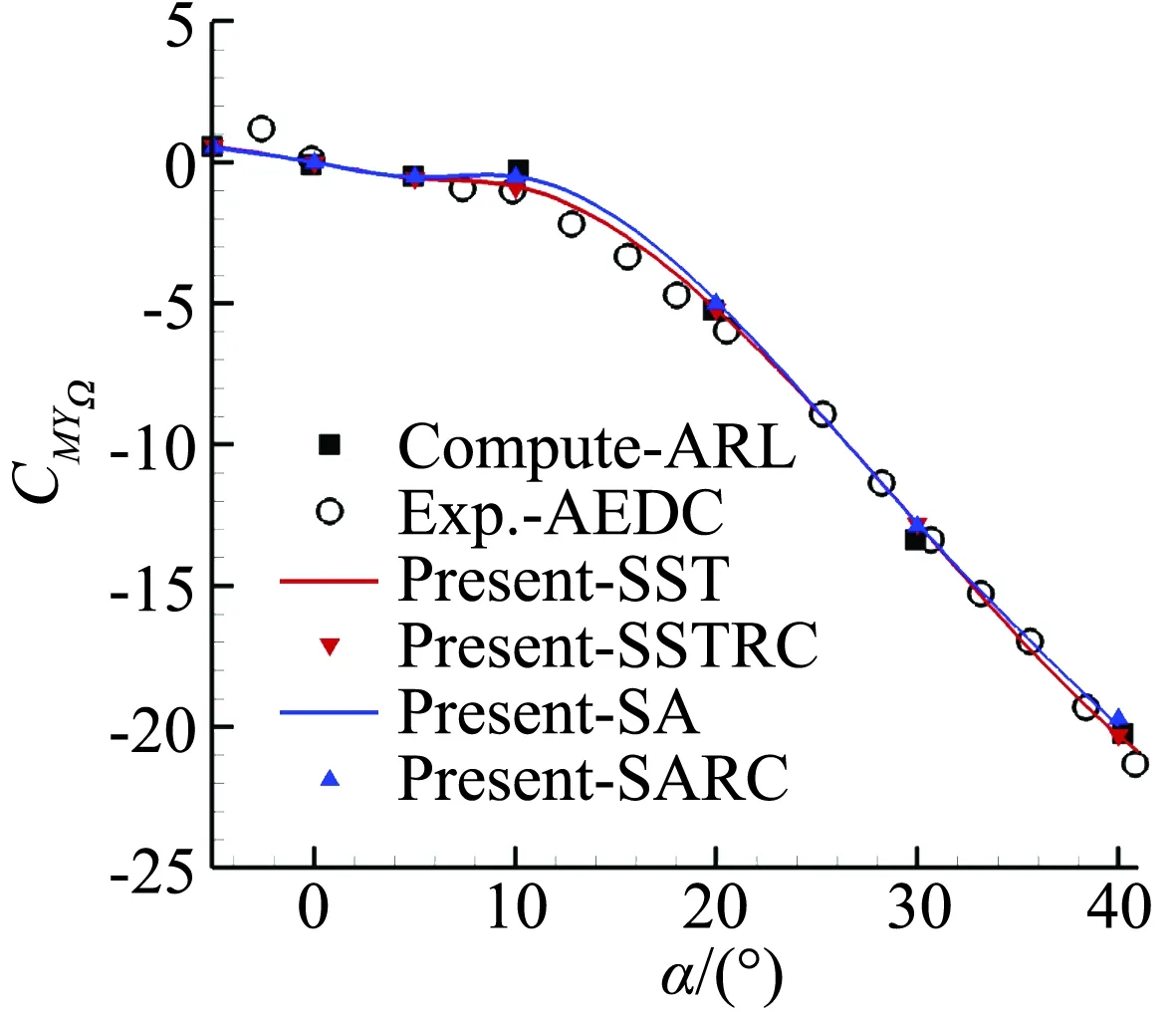
(a) 侧向力矩旋转导数CMYΩ

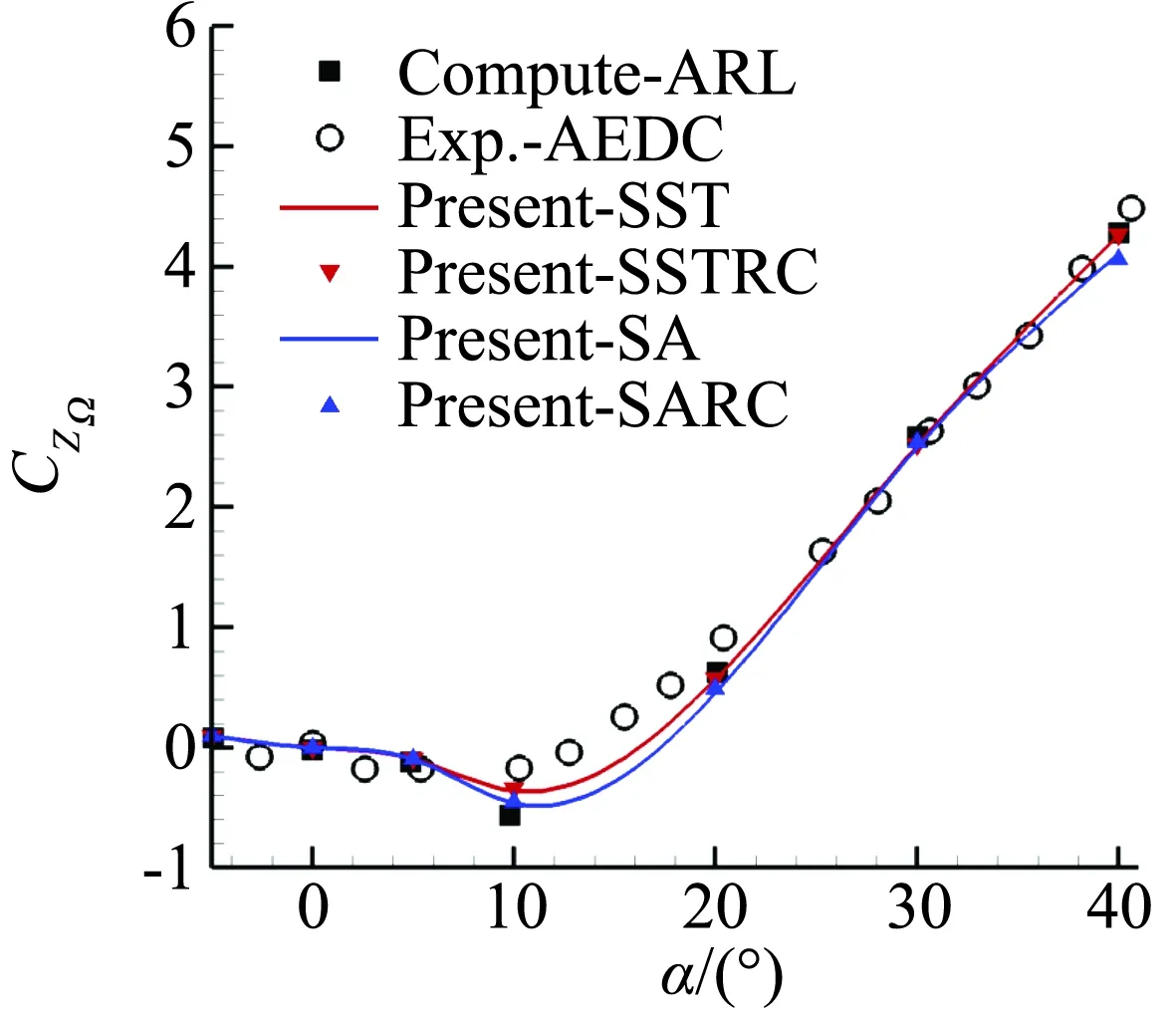
(b) 侧向力旋转导数CZΩ

对比SA、SST湍流模型及修正后的SARC、SSTRC模型可知，弯曲和旋转修正后的计算结果基本与原始模型重合，在实验和ARL结果的分散区间内。侧向力和力矩旋转导数差异主要在α=5°～20°，侧向力矩旋转导数SA偏大，与SARC最大偏差5.6%；侧向力旋转导数SA偏小，与SARC最大相差4.5%，由于5°～20°迎角范围侧向力和力矩旋转导数在零值附近，绝对差量很小，在图中体现不明显。

2.2 工程估算与数值模拟结果对比

工程估算方法是通过风洞实验数据或数值模拟数据，整理归纳出具有理论解析表达式的形式，应用于工程设计中。早期的学者对超声速旋成体马格努斯特性总结了很多工程估算方法，得到了很多规律性结论，如马格努斯力矩导数随马赫数增加(Ma=1-2.5)呈线性变化[21]，随船尾角增加呈非线性变化等[22]，对于本文这种带翼外形，选取四组典型估算公式进行分析，以考量工程估算方法的适用性。

1) Martin公式：

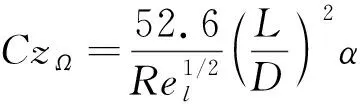
2) Kelly和Thacker公式：

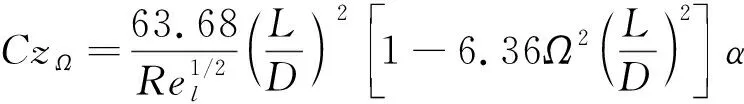
3) Vaughn和Reis公式：

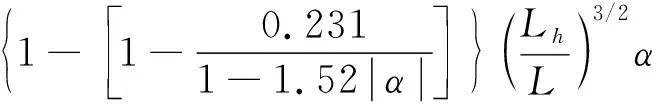
4) 吴承清提出的公式：

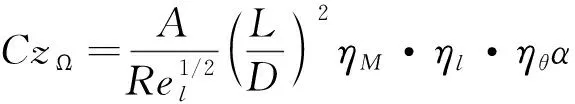
式(8)-(11)中的各参数定义见文献[20-22]，图4给出了工程估算方法与本文计算的侧向力旋转导数CZΩ随迎角变化曲线，可以发现：1) 工程算法中CZΩ随迎角α多接近线性分布，数值计算的CZΩ随迎角α非线性变化未能体现；2) 数值模拟与工程估算结果在整个迎角范围α=5～40°差异都很大，不满足工程估算公式可用性标准(误差<15%)，且随着迎角的增加差异越来越大；3) 分析差异原因可能是工程估算多是针对旋成体(尖拱+圆柱、尖拱+圆柱+船尾)外形，对于本文翼-身组合外形，弹翼的存在引入很大误差，弹翼的影响不可忽略，导致工程估算方法失效。

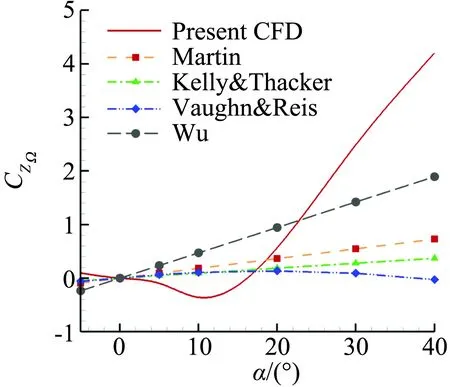
图4 不同方法得到的侧向力旋转导数变化曲线Fig.4 Comparison between CFD and estimation methods for CZΩ

2.3 沿轴向弹身表面压力及摩阻分布

图5给出了t=T、α=5°、40°背风区典型周向角下弹身表面沿流向的摩阻分布，从图中可知α=5°时摩阻系数变化平缓，系数范围[0.75，4]，从头部到尾翼前缘逐渐减小，只在肩部有一次转折，翼-身干扰使尾翼所在截面摩阻略有增加；α=40°时摩阻抖动很大，系数范围[-0.2，1]，大迎角和旋转使弹身表面流场变化剧烈，摩阻系数无明显规律。

比较两湍流模型可知，SA计算的摩阻系数比SST偏大；比较修正模型与原始模型可知，左右两侧摩阻系数差异都不大，只在弹体尾部区域有微小差异，而且摩阻本来就是小量，对全弹的影响很小。

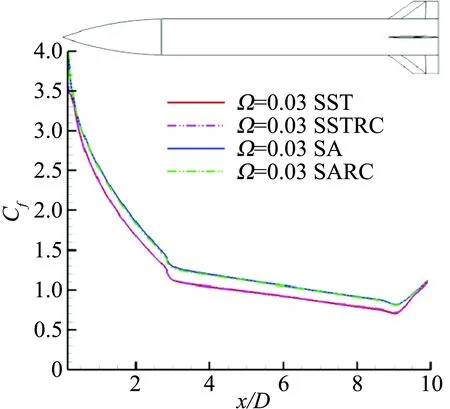
(a) θ=45°，α=5°

图6给出了t=T、α=5°、40°背风区典型周向角下弹身表面沿流向的压力分布，从图中可知α=5°时从头部到尾部为膨胀-压缩-膨胀过程，p/p∞范围[0.75，1]；而α=40°时从头部到尾部先膨胀-压缩，随后恒压段，最后再膨胀-压缩，由于弹体对来流的遮挡效应更强，压力系数明显减小，p/p∞范围[0.18，0.35]。

比较修正模型与原始模型可知，α=5°时SSTRC模型比SST模型计算的压力略小；α=40°时SARC模型比SA模型计算的压力稍大，差异主要在弹身后部及尾部，由于背风区压力量值很小、左右两侧压力抵消作用，全弹侧向力系数原始模型与改进模型差异不大。

2.4 沿周向截面和对称面空间流场分布

图7给出了t=T、α=40°、x/D=8截面SST和SSTRC模型空间压力云图及流线分布。从压力分布

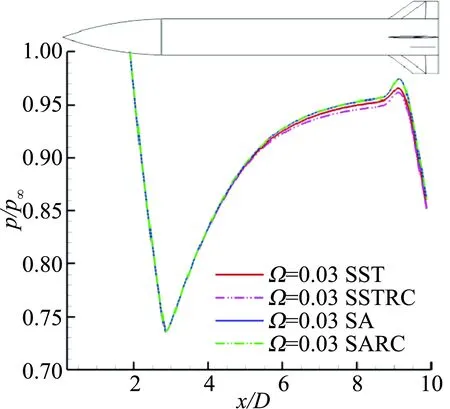
(a) θ=45°，α=5°

(b) θ=45°，α=40°

(a) SST

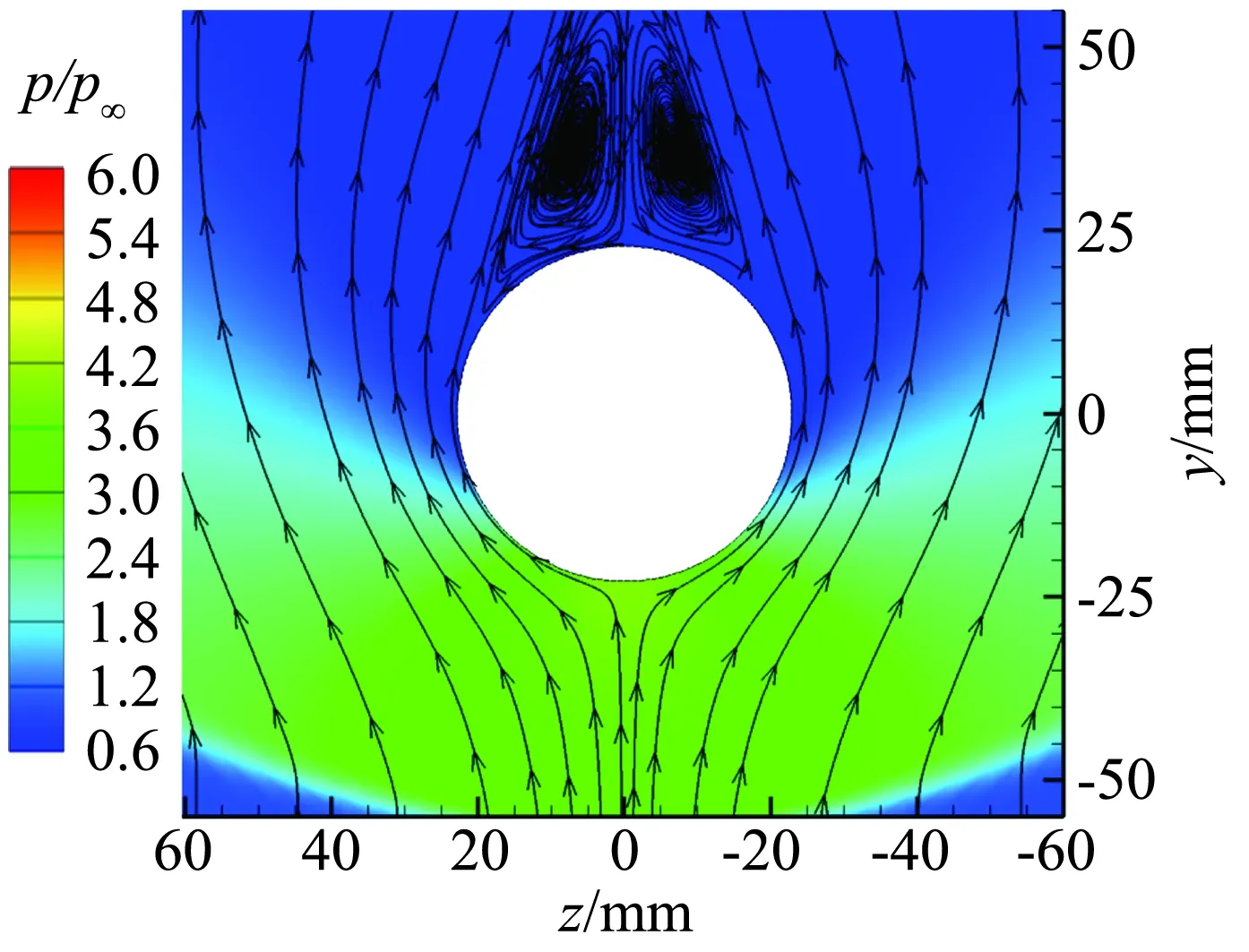
(b) SSTRC

可知头部激波向后发展，在弹身尾部迎风区存在很大

的弧型激波，背风区为膨胀区域，压力云图左右两侧差异不明显。而流线分布不再对称，正向旋转使弹体左侧速度向下，而正迎角时来流速度分量向上，两者相互阻碍使流线更脱体，易于分离；右侧旋转速度与来流同向，流线更贴体，不易分离，分析认为这是分离涡左侧比右侧大的原因。对比两模型结果可知，背风区SSTRC捕捉到的分离涡比SST大，可见弯曲和旋转修正使模型对分离流动的抑制能力减弱。

图8给出了t=T、α=40°、对称面SA和SARC模型计算的马赫数云图分布。可以看到两模型模拟到的头部激波、背风区膨胀波及舵上二次压缩激波基本相同，主要差异在弹体底部，SARC计算的底部低速区更大，即修正模型预测的底部分离区更大，恢复区更长。

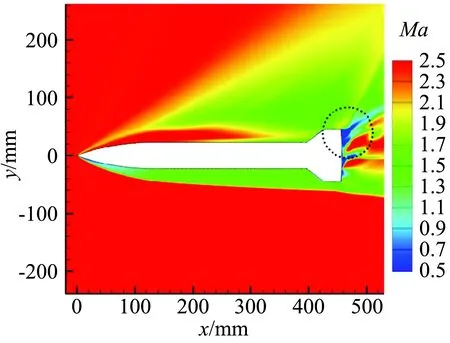
(a) SA

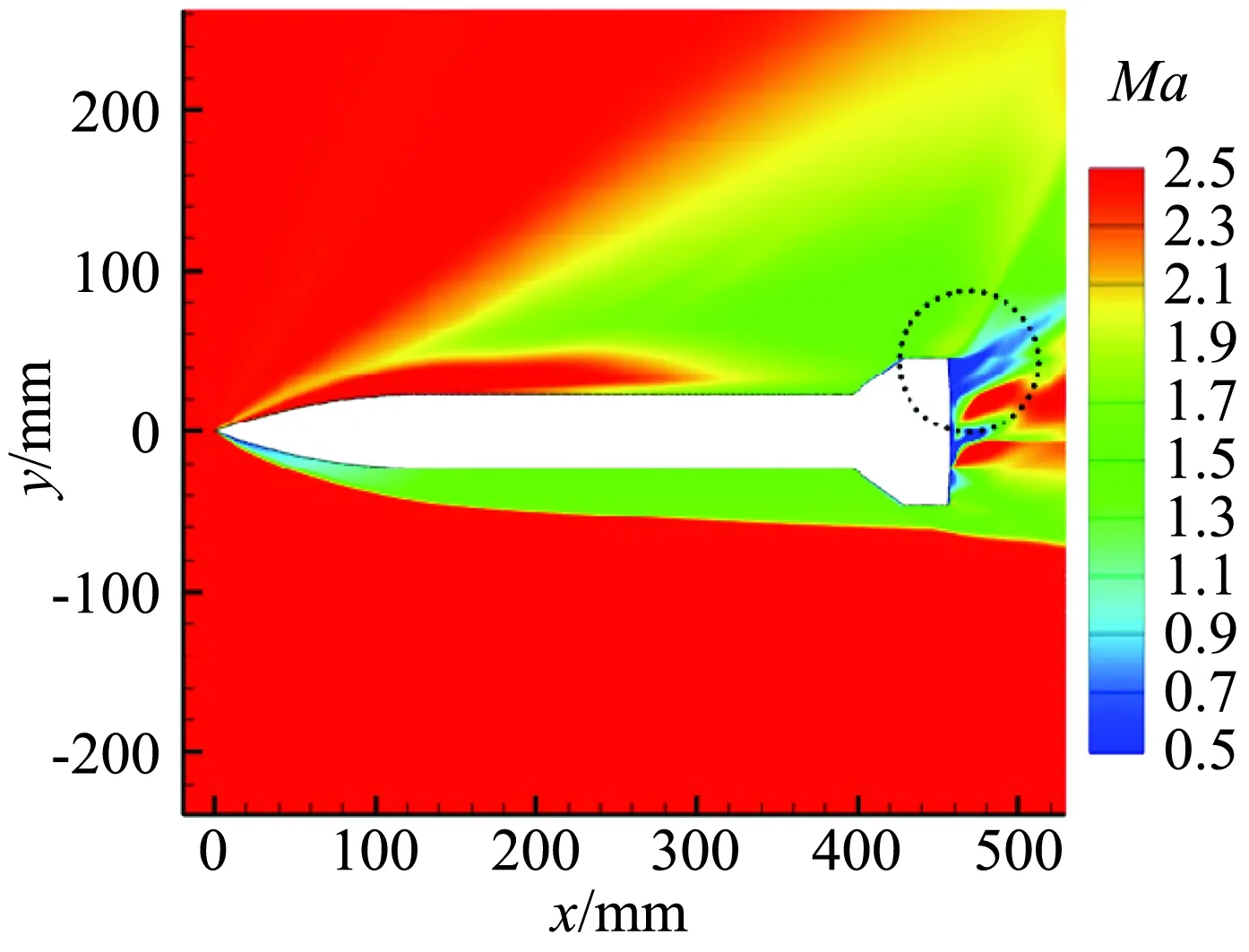
(b) SARC

3 结 论

本文采用完全时间相关的非定常N-S方程，对超声速带翼旋转弹箭开展计算，研究了弯曲和旋转修正的湍流模型SARC和SSTRC对弹箭旋转气动特性和流场结构产生的影响，通过数据分析得出以下结论：

1) 对全弹侧向动态特性而言，弯曲和旋转修正的湍流模型与原始模型精度相当，侧向力和力矩旋转导数最大差异<6%，工程估算方法不适用于本文翼身组合外形。

2) 对流场结构而言，修正模型使物面压力左右两侧同时偏大或偏小，与原始模型相比并没有加剧或削弱不对称效应，因此全弹马格努斯特性变化不大，弯曲和旋转修正模型预测的分离区更大，对分离流动的抑制能力减弱。

3) 修正模型与原始模型结果差异不大的分析有两点：一是原始模型预测结果已经很好，改进模型提升效果不明显；二是当前计算工况下逆压梯度引起的流线弯曲占主导，大于旋转和弯曲效应影响。修正模型对旋转弹箭的适用性还需做更多的研究。