基于曲柄滑块机构变刚度关节的设计与分析

，，

(苏州大学机器人与微系统研究中心，江苏 苏州 215000)

0 引言

变刚度关节的刚度调节功能是由电机驱动相应的刚度调节机构，通过改变柔性体的结构或力臂来实现。依照调节刚度部件的不同，变刚度关节可分为弹簧类[1-4]、磁铁类[5-7]和橡胶垫类[8-9]。其中，弹簧类研究最普遍丰富，可分为扭簧类、弹簧片类和圆柱(拉、压)弹簧类。

其关键技术难题主要集中在2点：第一，变刚度关节机构原理突破难；第二，变刚度关节轻量模块化难。从刚度调节机构来看，能够实施的机构有凸轮棍子机构、滑轮组合、齿轮齿条组机构和滚珠丝杠机构等传统传动机构，缺少更简洁的传动机构。

针对目前变刚度关节研究存在的机构方面的问题，提出一种以改变悬臂梁臂长为变刚度的力学模型，以曲柄-滑块机构为刚度调节机构的新型变刚度关节，并为此进行了变刚度关节的结构设计、数学建模和仿真实验分析。

1 变刚度原理

变刚度关节的关键部件是刚度调节机构和柔性构件。该方案中采取一种较为便宜易得、工艺较为成熟的板簧作为柔性元件，采取的刚度调节机构为结构简单易控的曲柄-滑块机构。

通过曲柄-滑块机构改变受力支点位置，以改变弹性元件有效的工作长度，这种刚度调节的机构原理如图1所示。其力学模型为悬臂梁，根据其挠曲方程，易得知其刚度：

(1)

从刚度表达式中可以知道，悬臂梁的刚度值与其臂长成非线性反比关系。悬臂梁的臂长越长，其刚度越小，反之，则刚度越大。图1和式(1)中，L为板簧有效工作长度；a为曲柄长度；b为连杆长度；φ为曲柄转角；s0为曲柄中心至板簧外力作用端水平方向距离；h为曲柄中心至板簧外力作用端竖直方向距离；s为曲柄中心至滑块距离；F为外负载力；E为板簧弹性模量；I为板簧惯性矩。

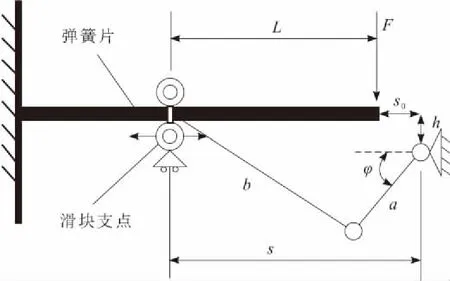
图1 刚度调节机构原理示意

2 关节结构设计

关节整体的三维建模如图2所示。该变刚度关节主要由4部分组成：位置驱动机构、刚度调节机构、柔性输出机构和柔性角度测量机构。其中，位置驱动机构由瑞士Maxon电机、同步带轮系和谐波减速器等组成。

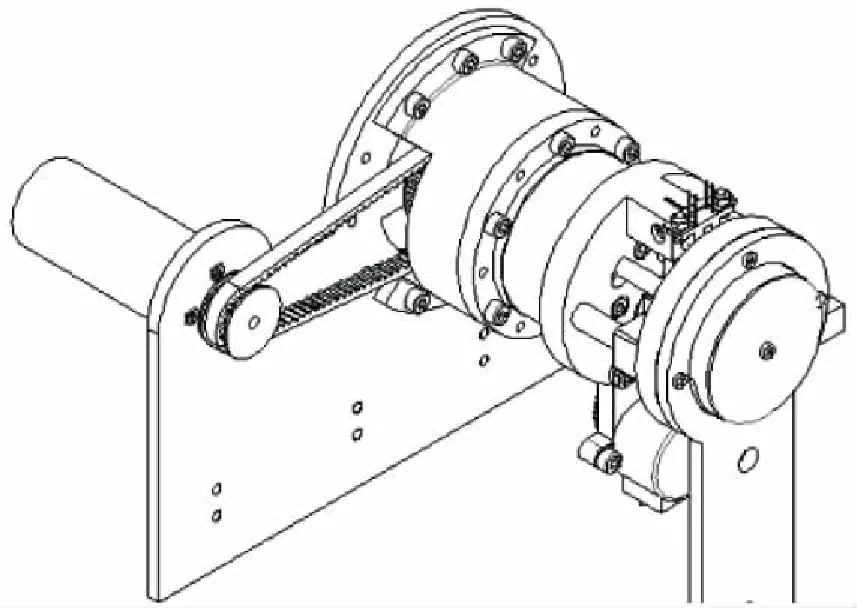
图2 完整关节模型

变刚度关节的刚度调节机构模块结构设计如图3所示，由输入支架、伺服电机、一级传动齿轮系、轴、曲柄板件、连杆板件、支撑滑块、十字型导向支撑输出件、1对连接柱、弹簧片、1对簧片夹持棒、1对限位保护柱、复位光电开关、复位光电开关保持架、光电开关挡板、输出轴套筒、码盘、码盘读头、输出盘，以及一些螺钉连接标准件等部分组成。

变刚度关节的刚度调节机理是利用曲柄滑块机构的运动特点，即输入为旋转运动，输出为直线往复运动，改变柔性元件受力支点位置即力臂长度大小，实现柔性元件弹簧片表现为不同的刚度。由于弹簧片承担着传递关节运动的承接作用，因此整个关节也具有不同的刚度特性。显然这种刚度特征的表现程度取决于弹簧片的刚度特性。具体表现为弹簧片的刚度系数越大，则关节刚度越大，反之，则关节刚度越小。从而可以通过调节曲柄滑块机构，使关节根据不同的实际刚度需求情况，表现为不同的刚度特征变化。

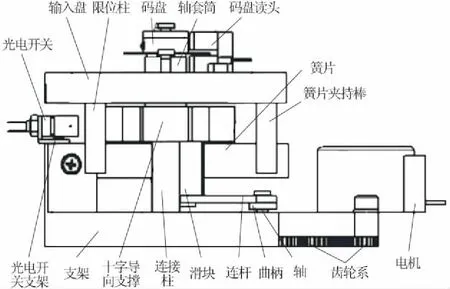
图3 刚度调节机构详细注解

码盘和码盘读头共同组成柔性角度测量机构。主要用于测出关节因外界冲击而产生的缓冲角度，与刚度调节机构相配合，实现对主动控制关节输出刚度特性的闭环控制。

3 数学建模

变刚度关节简化轮廓如图4所示。图4中，T为关节外力矩；R为关节半径；θ为关节偏角。已知关节的刚度定义为所受微小外力矩与关节产生的微小角度的比值，定义式[3]为：

(2)

图4 变刚度关节简化轮廓

曲柄滑块作为平面连杆机构设计中常用的结构，其结构见图1，由几何关系可推导出曲柄与滑块的位置对应关系式：

m1scosφ+m2sinφ-m3=s2

(3)

其中，m1=2a,m2=2ah,m3=a2-b2+h2。 曲柄旋转中心与板簧中轴线设计为共处一条线上。取h=0，整理可得：

(4)

由图1可知板簧有效工作长度：

L=s-s0=

(5)

已知板簧刚度公式：

(6)

δ为板簧变形角。由板簧受力情况与关节扭转之间关系，可知：

dT=dF·R

(7)

代入关节刚度定义式可得：

(8)

一般情况下，板簧和关节的扭转变形通常都是微小的，则有：

dδ=dθ·R

(9)

从而求得板簧刚度至关节刚度的函数映射关系：

(10)

相反，在关节的较大扭转变形的情况下，则有：

(11)

从而可求得板簧刚度至关节刚度的函数映射关系：

(12)

由式(5)和式(6)可得板簧刚度与曲柄角位置之间的关系式：

(13)

同理，在微小变形情况下，可得关节刚度与曲柄转角的关系：

(14)

在较大变形情况下，关节刚度与曲柄转角及关节偏转角度的关系：

(15)

4 仿真实验

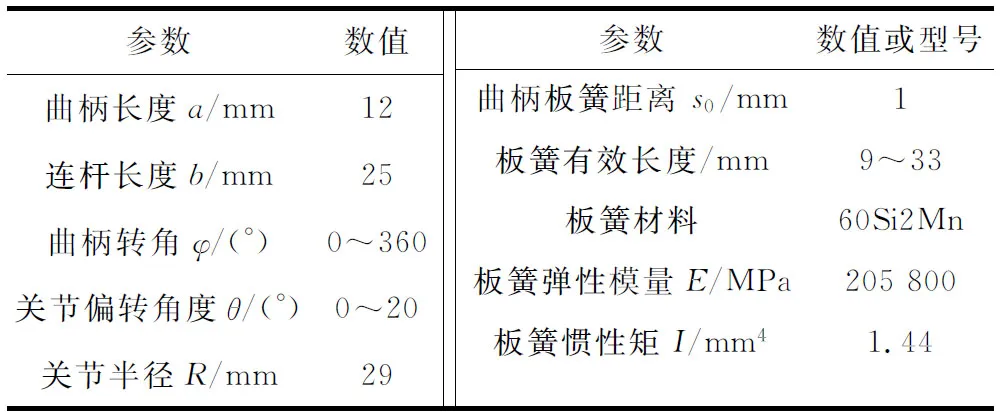
已经搭建的刚度调节机构及关节样机如图5所示。变刚度关节机构参数的详情如表1所示。

图5 变刚度关节样机机械部分

板簧工作长度分别为10 mm,15 mm,20 mm时，关节刚度与关节偏转角度之间的关系曲线如图6所示。由图6可知，在关节允许偏转角0～20°的范围内，关节刚度值未发生显著的变化，3条曲线的最值比(最小值/最大值)分别为0.988 8，0.989 2，0.988 8。因此，该变刚度关节在正常工作情况下，关节刚度基本保持稳定。

图6 关节刚度与关节偏转角度之间的关系曲线

在板簧有效长度范围内(9～33 mm)，关节刚度的变化曲线如图7所示。由图7可知，在板簧有效长度9～15 mm的范围内，关节刚度值随着板簧有效长度的增大而迅速变小；在15～33 mm的范围内，关节刚度值随着板簧有效长度的增大而缓慢变小；33 mm以后，关节的刚度则基本保持不变，考虑到对关节刚度的控制精度问题，选择此范围内的有效长度进行控制，可得到较为理想的刚度值。

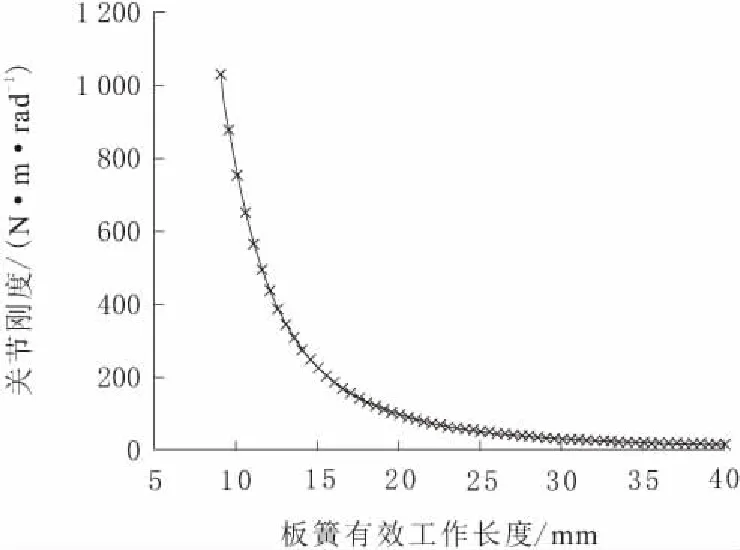
图7 关节刚度与板簧有效长度之间的关系曲线

在曲柄输入转角(0～360°)范围内，关节刚度的变化曲线如图8所示。由图8可知，在曲柄转角0～180°的范围内，关节刚度随着曲柄转角的增大也均匀变大；在180～360°的范围内，关节刚度则随着曲柄转角的增大而均匀变小；该曲线的前后半部分是对称的。因此，通过调节曲柄滑块机构输入转角即可实现关节刚度的调节。

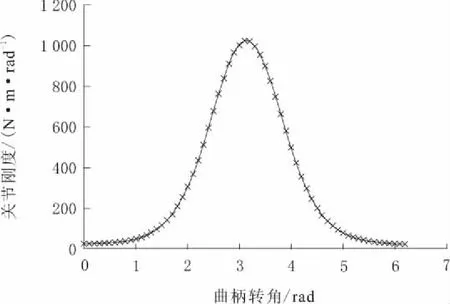
图8 关节刚度与调节机构输入转角之间的关系曲线

综上可得，关节刚度受外在冲击影响较小，随板簧有效长度的增大而减小，为控制关节刚度，可根据其对称变化特性选择较小功耗的曲柄转角来实现。

5 结束语

阐述了基于曲柄滑块机构的变刚度关节变刚度原理、结构组成、刚度调节机理和数学模型。分析了变刚度的过程和特点，获得了关节刚度的数值特性，理论上验证了该方案的可行性。

后续的工作则集中于实验系统电气部分的搭建，以及研究设计变刚度关节的控制系统，确保关节刚度可调及位置的精确控制。