基于多元回归模型的斜坡影响因子分析

覃 强, 董建辉

(1.中国地质科学院探矿工艺研究所，四川 成都 611734； 2.中国地质调查局地质灾害防治技术中心，四川 成都 611734； 3.成都大学建筑与土木工程学院，四川 成都 610106)

0 引言

自20世纪80年代以来，我国的地质灾害进入了一个新的活跃期，特别是“5.12”汶川地震以后，地质灾害频频发生，规模也越来越大，特别是滑坡灾害的存在，严重威胁着当地群众生命财产安全和阻碍当地经济的发展。目前国内研究人员积极运用各种试验和方法开展探索滑坡时空的预测、滑坡灾害的致灾因素和变形破坏机理等方面研究，此类型的研究对于滑坡灾害的预防及治理研究有着极其重要的社会意义和经济价值。

但由于滑坡灾害本身是一个复杂的系统，有着较多的不确定性因素，滑坡时空预测的研究仍是领域内学者们的重要研究方向之一。随着我国基础建设的高规模、高规格、高速发展，如建筑场地和道路建设、矿产开采、水利水电工程开发，这些工程建设经常遇到边坡问题逐渐演化成滑坡灾害问题，因此对于其致灾因素也越来越关注，也越来越重视。目前运用数学理论模型进行边坡稳定性分析的文献越来越多[1-5]，对于运用多元回归分析进行滑坡预测分析也有了一定的深度和广度[6-8]，也有学者运用多元非线性回归分析对单体滑坡进行了滑动时间预测[10-12]。但是运用多元非线性回归分析对斜坡的影响因子研究相对较少，通过本文的研究做到摸清滑坡灾害的影响因素的变化，从而进一步了解滑坡的各种特性。

1 多元回归模型

多元回归模型是以时间序列模型为基础展开的，而统计分析理论作为时间序列模型的基础，应首先明确某个事件的自变量和因变量之间存在关联，通过寻找一个能表达自变量与因变量间的函数关系来阐述。变形监测模型中运用回归模型的案例较多，其原理是利用监测数据来明确回归方程中的自变量系数，目前常用的方法有最小二乘法，利用该方法建立的模型属于统计数学模型中的“后验模型”[13]。

根据实际的监测数据建立回归模型，变形组(自变量)(X1t,X2t,X3t,…,Xkt;Y)(t=1,2,3,…,N;N≥k)的N组观测数，Y为变形效应量。

建立线性回归方程：

Y=B0+B1X1+B2X2+…+BkXk

(1)

将观测数据进行最佳拟合，求出自变量系数(B0,B1,B2,…,Bk)，建立自变量(X1,X2,X3,…,Xk)与Y变形效应量之间的数学模型，这是典型多元回归方程。在实际案例运用过程中证明，多元回归方程中大部分情况是非线性的。多元线性回归方程可以是指数、多项式等等形式，以下以指数和多项式为例。

(1)对于指数形式的回归模型

lnW=B0+B1lnZ1+B2lnZ2+…+BtlnZt

(2)

只要令Y=lnW,X1=lnZ1,X2=lnZ2,…,Xt=lnZt，则该指数形式回归模型就转化成多元线性回归问题。

(2)对于多项式的回归模型

(3)

只要令X1=W1,X2=W2,X3=W12，X4=W22,X5=W1W2,…，则该多项式回归模型就转化成多元线性回归问题。

经典多元回归方程的计算值和实测值的拟合程度以及预报值的精度检验指标主要有剩余平方和Q、回归平方和U、复相关系统R以及剩余标准差S等。

2 工程案例

2.1 影响因子选取

对于回归模型运用到斜坡中，其关键就是选择合理的影响因子和正确的数学表达统计模型。首先要对监测数据进行一定的预处理，剔除误差，再利用回归理论建立影响因子(自变量)和变形量(因变量)之间的数学统计模型，通过数学统计模型的试算，进一步得到斜坡的变形规律以及影响因子的比重。

本文以某水电站水库堆积体斜坡为例，该斜坡从2006年开始进行变形观测，一共埋设7个深部位移监测孔，编号分别为IN-1～IN-7，其中IN-1为自动化监测孔，此次暂未统计深部位移监测孔IN-1，因此总共有6个变形量(因变量)，详见图1。根据对该堆积体斜坡的现场调研和相关分析，自2006年以后该斜坡的外部条件没有任何改变，造成堆积体斜坡产生变形的主要影响因素为库水位升降、降雨、时间效益等3个影响因素，统计的时间段为2006-2012年，其时间段经过了2008年“5.12”汶川地震，详见图2、图3。

从变形成因分析，可以将变形量(自变量)分为3部分:库水位分量δH、降雨分量δJ、时间效益分量δT，即：

δ(δX、δY或δZ)=δH+δJ+δT

(4)

2.2 多元回归建模步骤

根据以上对堆积体斜坡的影响因子选取以及回归模型的相关叙述，整理堆积体斜坡的深部位移监测数据和监测数据的相关影响因素资料，建立一个预测精度高及最佳拟合的多元回归模型，而且相关影响因子系数对于变形监测数据则具有很强的解释性，这也是本文所探索的核心内容。多元回归模型的技术路线如图4所示。

(1)整理变形监测资料。整理堆积体斜坡的变形监测数据、观测的影响因子的监测数据。

(2)数据的可靠性检验和预处理。在对堆积体斜坡的监测体系进行日常观测中，难免会出现差错和误差等一些额外的情况，因此有必要对监测数据进行可靠性检验，主要是分析监测数据的连续性和关联性，结合实际情况选择不同的可靠度检验方法，如果发现异常点应采取相关处理措施进行预处理。

(3)影响因子选择。根据现场调查以及资料收集，确定主要影响因子集合，对其做多元回归分析计算。

(4)确定回归方程形式。在明确影响因子之后，选择多元线性回归方程的形式进行试算，可以是指数、多项式等等形式。

(5)检验回归模型。回归方程形式确定之后，应对每个回归方程进行相关可靠性检验，如有不能满足检验的回归方程或组合，则立刻调整回归方程并重新进行检验。

(6)经过回归方程的试算以及相关检验，最终确定合适的回归模型。

(7)根据回归模型，进行相关解释。

2.3 多元回归建模

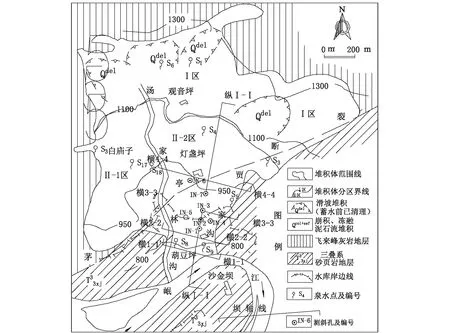
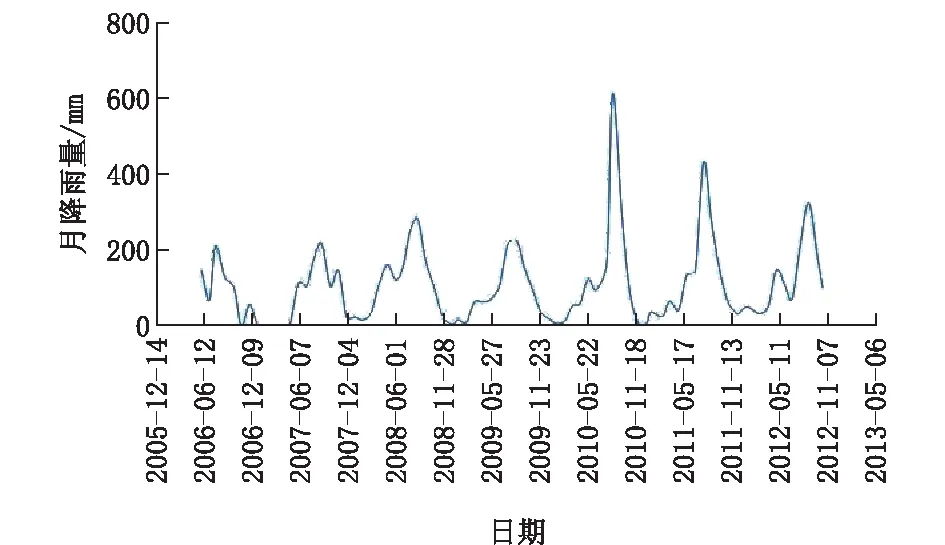
图2 月降雨量-时间变化图

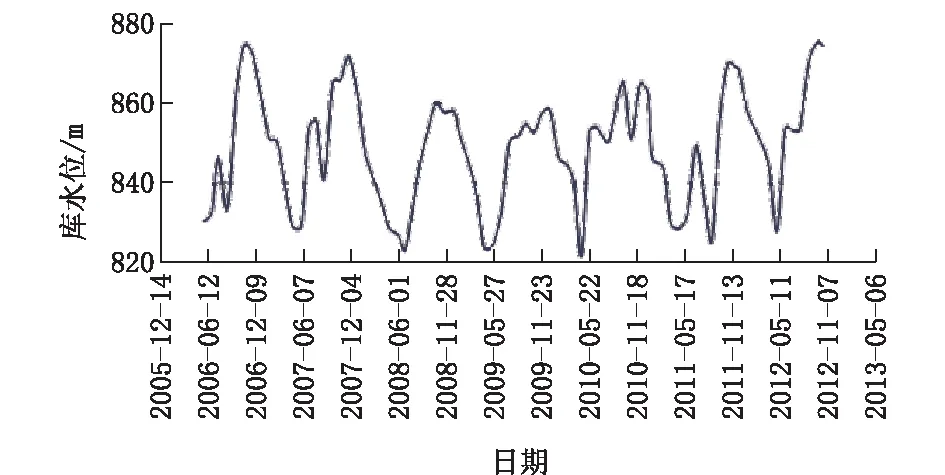
图3 库水位-时间变化图

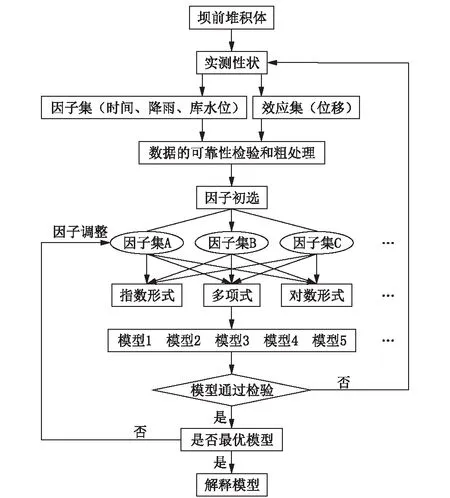
图4 多元回归模型流程图

针对某一水电站水库堆积体斜坡的6个深部位移监测孔数据，首先进行数据的可靠性检验和预处理分析。由于本文所用的6个深部位移监测孔均为人工观测孔，故地表的孔口累计位移误差较大，所以首先应对其进行平滑处理。将每年的监测数据按照自然月份分为12个周期，然后对其监测数据进行分段趋势预处理，结果如图5和图6所示。从观测时间段来看，可以将监测数据分为汶川地震前和汶川地震后两个时间段，即2006年5月-2008年4月和2008年5月-2012年10月。

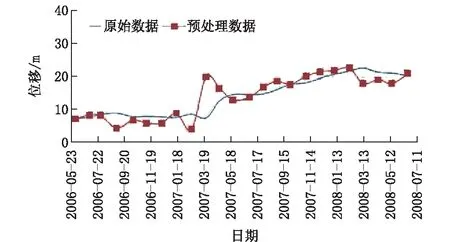
图5 IN-2地表位移预处理-时间关系曲线(地震前)

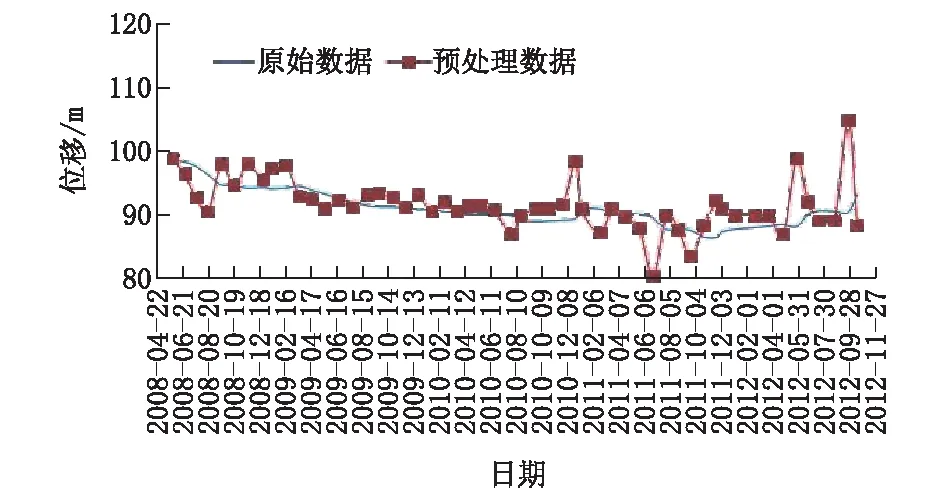
图6 IN-2地表位移预处理-时间关系曲线(地震后)

根据多元回归建模步骤所示，本文试算不同的回归方程形式，结果发现预测精度高及最佳拟合的多元回归模型为指数函数。回归方程表达式如下所示：

lnY=aX11+bX22+cX33+C

(5)

根据影响因子的分析，我们可以假设：Y为深部位移孔口的累计位移量，以每个月的监测数据作为统计数据；X11为时间效益因子，X11=ln(1+0.01X1)，X1为观测次数，单位为月数；X22为降雨量因子，X22=lnX2，X2为每个月的降雨量；X33为库水位因子，X33=lnX3，X3为每个月月底的库水位。

我们采用Eviews专业统计软件进行相关回归方程统计以及可靠性检验工作，以IN-2为例，计算结果见表1。

根据IN-2的回归方程的Eviews计算结果，回归模型的拟合结果如下：

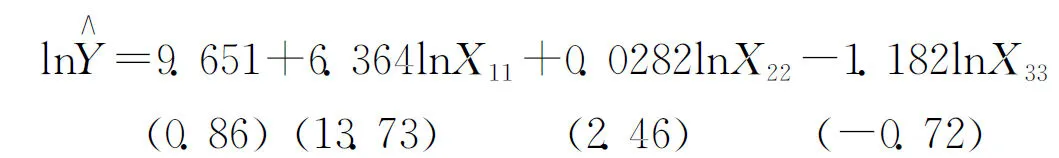
(6)

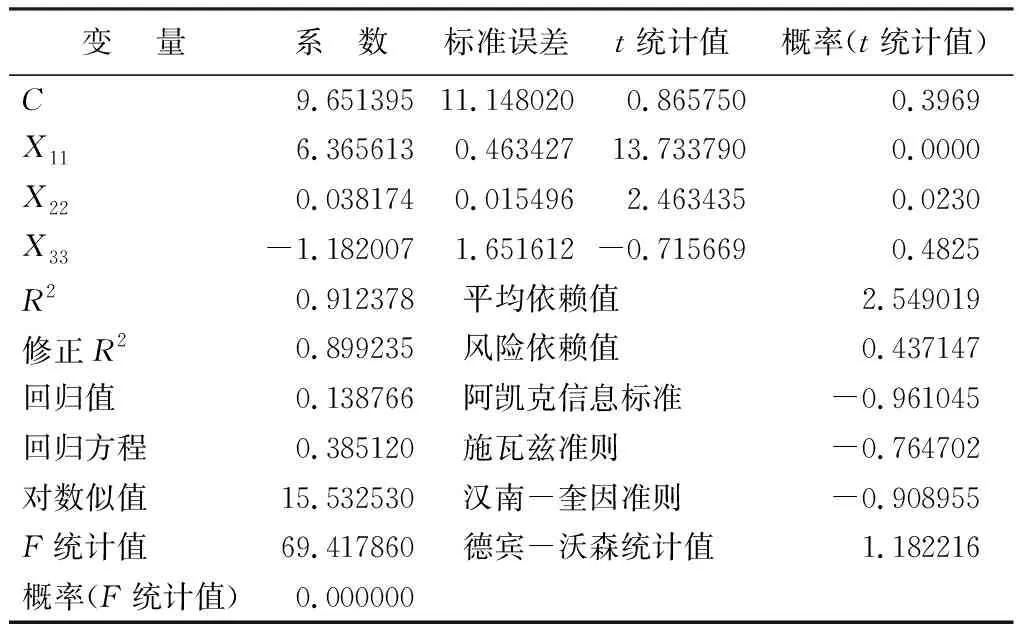
表1 回归方程输出结果

结合表1和公式6，其中括号内的数值表示t值，将根据假定的0.05显著性来判断F值，从计算结果来看回归系数的估计值，结果基本无显著性，其中模型结果的拟合度(R2)相当高，其数值为0.91，这说明选择的模型较合理；F值为69.42，说明影响因子可能存在着共线性。我们利用klein判别法来分析影响因子之间的共线性。从表2所提供的影响因子之间相关系数来判断，各影响因子之间的关联系数都很小，我们认为各影响因子之间不相关。

表2 “5.12”汶川地震前IN-2相关系数矩阵

2.4 回归数据分析

根据多元回归模型流程图，我们同样可以推导出其余的5个深部位移监测孔的孔口累计位移与各影响因子的多元回归方程，其计算结果详见表3和图7～图9。

如图7～图9所示，从该水电站水库堆积体斜坡的影响因子与深部位移监测点孔口累计位移的回归方程系数关系分析出：

(1)汶川地震后相对于汶川地震前的时间效益影响有所变小。

(2)汶川地震后相对于汶川地震前的时间降雨量影响有所变小。

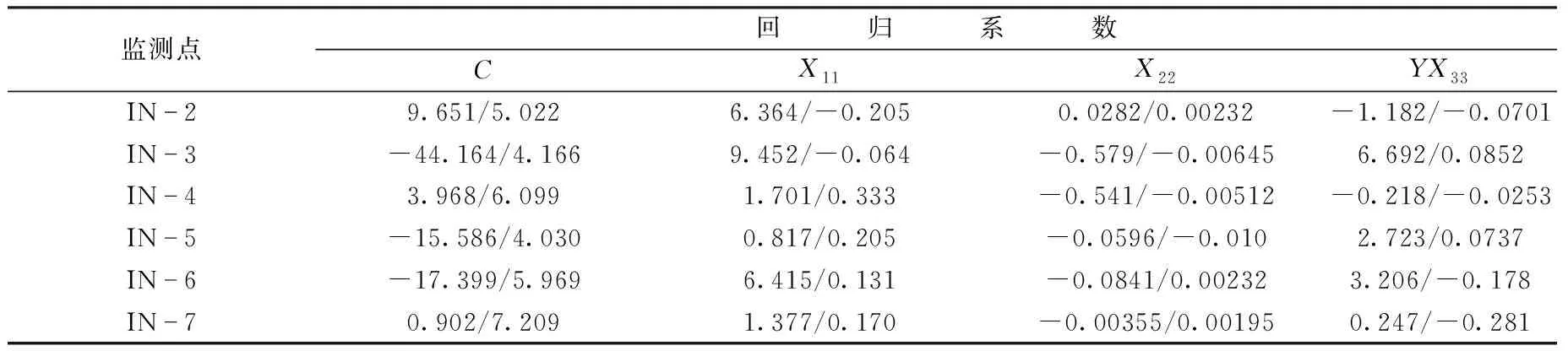
表3 汶川地震前后多元回归方程系数统计

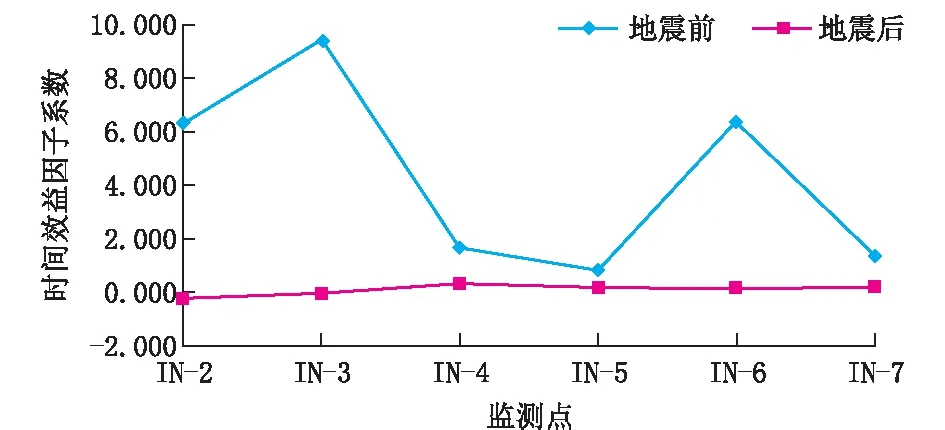
图7 各监测点时间效益因子系数曲线图

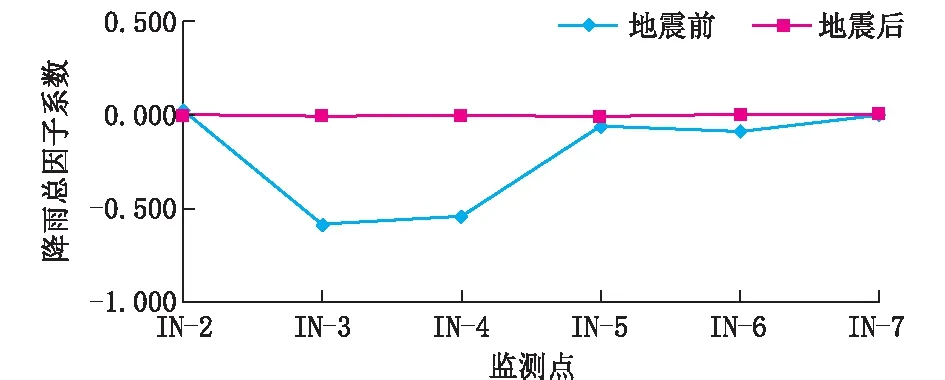
图8 各监测点降雨量因子系数曲线图

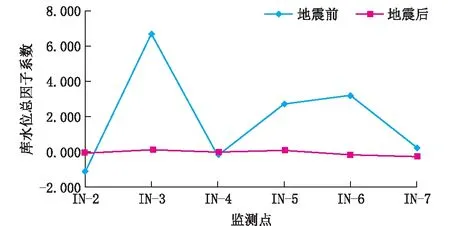
图9 各监测点库水位因子系数曲线图

(3)汶川地震后相对于汶川地震前的时间库水位影响有所变小。

(4)绝大部分监测点回归方程中的C值变小。

(5)汶川地震后降雨量的影响在增加，而时间效益和库水位的影响在下降，应当进一步加强降雨的观测。

3 结论

结合工程案例，对该水电站水库堆积体斜坡的影响因子进行了分析和选取，建立了相关多元回归模型把影响因子与监测位移量进行了量化，经过检验和可靠度分析，其拟合结果较为合理，分析了影响因子在汶川地震的变化，应当进一步加强相关影响因子的监测。该方法在一定程度上解决斜坡影响因子量化的问题，但要使用准确的数学模型来模拟研究斜坡稳定性问题，并达到采用精确的预报模型来预测影响因子的发展规律还相当困难，特别是斜坡的稳定性受外界条件影响较大，如何在该模型中增加影响因子、影响因子确切取值及通过模型分析计算结果结合斜坡实际情况相分析、比较等问题，有待于今后进一步的深入研究。