基于全桥气弹模型风洞试验的大跨度斜拉桥抖振响应研究

王晓冬，曾宇

（中交公路规划设计院有限公司，北京 100088）

0 引言

大跨度斜拉桥主梁一般采用钢箱梁，其结构质量和阻尼比相对混凝土梁要轻、要小，结构频率也较小，因此在自然风的作用下发生振动的幅度要高于混凝土梁，可能会对桥梁施工和运营带来不利影响，因而准确把握结构在自然风作用下的抖振响应对于抗风设计尤为重要。抖振响应是抗风性能评估的重要部分，尤其对于斜拉桥的最大悬臂施工状态，其结果直接关系到施工安全性和可行性。抖振响应分析主要依靠理论分析和风洞试验等手段，最为准确的是在模拟大气边界层紊流中借助全桥气弹模型试验直接测量。从目前的研究情况来看，对于大跨度斜拉桥的抗风研究，尤其是最不利的最大悬臂施工状态的全桥气弹模型风洞试验少有报道。此外，对于斜拉桥施工态的抖振响应计算虽然也有相关成果[1-4]，但目前抖振计算理论和规范要求只能考虑正交风作用，对于斜交风下的抖振响应必需借助风洞试验或现场实测才能完成[5-8]。尽管斜交风下的抖振研究成果表明，1 000 m主跨量级大跨度桥梁抗风设计需要考虑斜交风影响，但对于常规的500 m跨度量级的斜拉桥来说，在抗风设计中是否考虑斜交风作用尚不明确，若也需要考虑斜交风的影响，将会加重设计任务，或者提升造价。

因此，本文以某主跨500 m量级大跨度混合梁斜拉桥为例，基于1颐100比例尺，制作了全桥气弹模型，在实现对大桥频率和振型准确模拟的基础上，在模拟大气边界层紊流场中开展了正交风和斜交风作用下的抖振响应测试，把握了大跨度混合梁斜拉桥运营状态和最大单悬臂施工状态的抖振响应特点，并由此计算了抖振内力，明确了此跨径下不用考虑斜交风的影响，为常规跨度斜拉桥的抗风设计提供了必要参考。

1 工程背景

某长江大桥为高低塔混合梁斜拉桥，桥跨布置为：39 m+53 m+48 m+520 m+53 m+5伊48 m，全长953 m。中跨主梁采用流线型钢箱梁，两个边跨采用混凝土箱梁，在桥塔附近设置钢混结合段。主梁宽31 m，高3.2 m（中心线处）；大桥的斜拉索采用空间双索面布置，锚固于主梁两侧风嘴位置处；大桥的桥塔采用混凝土材料和不等高设计，高塔高210 m，矮塔高123.5 m，以适应两岸不同地形的需求。中跨钢箱梁主梁标准断面如图1。

图1 混合梁斜拉桥钢箱梁主梁断面图Fig.1 The steel box section of cable-stayed bridge with hybrid girder

2 风洞试验概述

全桥气弹模型能够更加全面的反映结构与空气相互作用的三维效应，获得的测试结果也更加接近实际桥梁。本文重点讨论在模拟大气边界层条件下的全桥气弹模型抖振响应测试。

全桥气弹模型的几何缩尺比定为1颐100，对应的风速比（模型试验风速与原型实际风速之比）为1颐10，对应的频率比（模型自振频率与原型桥梁自振频率之比）10颐1。按照此比例设计的模型全长9.53 m，其中矮塔高1.235 m，高塔高2.10 m，钢箱梁主跨长度为5.2 m。根据模型的设计尺寸，安装后其在风洞中的空气阻塞度小于3%，符合抗风规范中对全桥气弹风洞试验阻塞度的要求。

全桥气动弹性模型各构件组成和实际桥梁保持一致，由主梁、桥塔、斜拉索及支座等构成，其中主梁和桥塔模型采用内部芯梁模拟刚度和木制外模模拟气动外形的传统方式。由于该桥跨中部分为钢箱梁，边跨部分为混凝土箱梁，为了满足结构的配重要求，中跨模型的芯梁采用铝材，而边跨模型的芯梁采用钢材制作。其中中跨部分主梁的相似刚度采用槽型铝质芯梁来提供；边跨部分的混凝土箱梁，其模型的相似刚度采用槽型钢质芯梁提供。安装在风洞试验中的全桥气弹模型如图2和图3，其中非接触式激光位移计安装在中跨斜拉索交界位置和高塔侧的1/4跨位置，以测试风致位移。

图2 全桥气弹模型风洞试验（成桥态）Fig.2 Wind tunnel test of full scale aero-elastic model(completed bridge condition)

图3 全桥气弹模型风洞试验（最大单悬臂）Fig.3 Wind tunnel test of full scaleaero-elastic model(thelongest cantilever condition)

模态测试所得成桥状态和最大单悬臂施工状态气动弹性模型的模态测试结果如表1和表2所示。从表中可以看出，模型重要模态的频率测试值与要求值吻合良好，结构阻尼比也在合理范围内，从而保证了模型结构动力特性与原型相似。

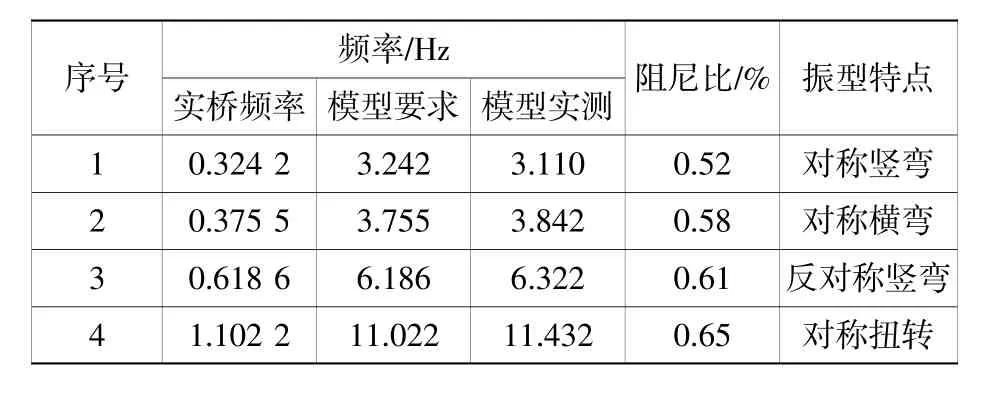
表1 成桥状态模态测试结果Table 1 Theresults of modal testsof the completed bridge condition

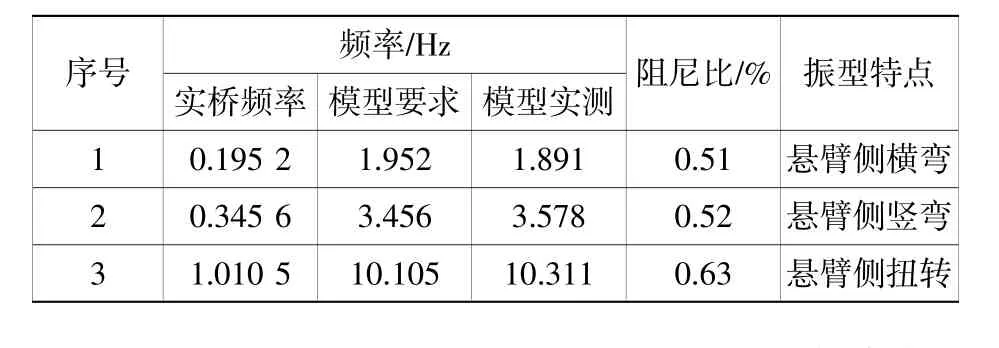
表2 最大单悬臂状态模态测试结果Table2 The results of modal testsof the longest cantilever condition

根据桥位区所在地气象站提供的风速资料，桥址区域地标类别为B类，风剖面指数琢=0.16。风洞试验风场应与桥址处的风场满足相似条件。风洞试验的风场模拟采用尖塔与粗糙元的形式进行。采用三维眼镜蛇风速仪对紊流场进行测试和校准，以获得平均风速剖面和紊流度剖面。紊流场测试结果表明，模型所在位置的风剖面图、紊流强度（Iu）剖面和模拟的B类地表大气边界层风谱，如图4，其与目标值吻合良好，满足抗风设计规范对于抖振试验大气紊流场特性的相关要求。

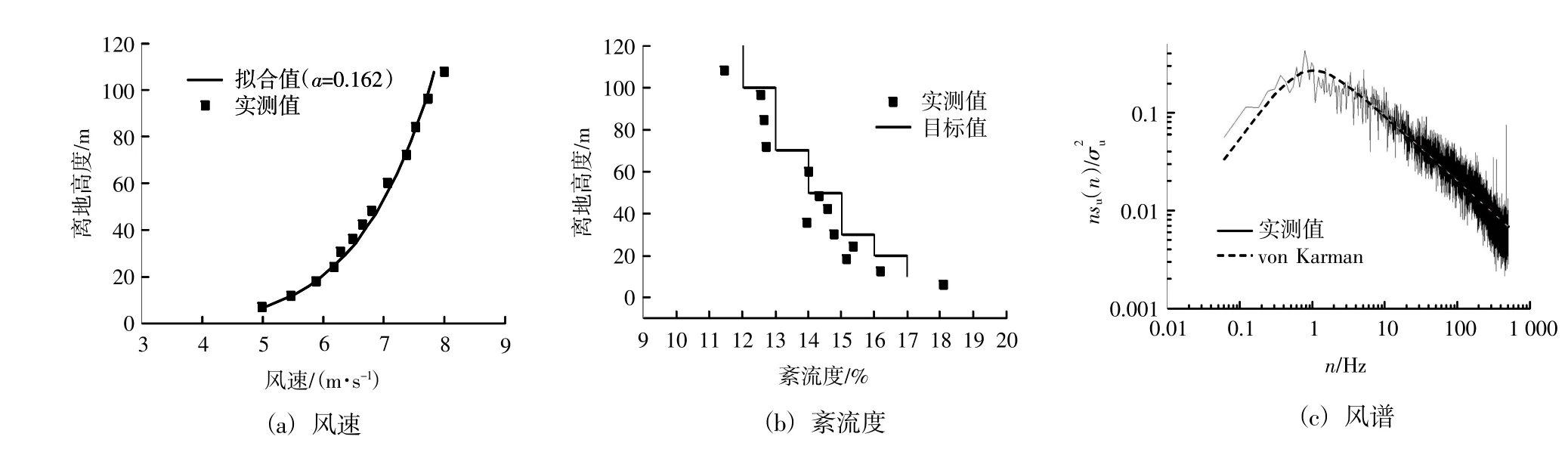
图4 风洞紊流场的风速剖面、紊流度剖面和风谱Fig.4 The profile of wind speed and turbulent intensity,and the wind spectrum of turbulence field

3 主梁抖振响应和抖振内力

成桥态0毅风攻角和0毅风向角（正交风）下的抖振响应曲线如图5。从中可以看出，成桥态主梁跨中响应值大于1/4跨的值，表明抖振受对称振型的影响显著，符合大跨度斜拉桥风致响应的一般规律。此外，最大单悬臂施工态则是悬臂端部主梁响应显著大于1/4悬臂长度位置，表明第一阶振型在抖振中占据主导位置，符合一般性规律。

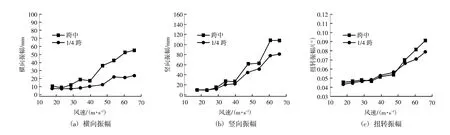
图5 成桥态抖振位移响应根方差（0毅风攻角0毅风偏角）Fig.5 The RMSof buffeting displacement in completed bridgecondition(0毅incident angle,0毅skew angle)

成桥及最大单悬臂施工状态下，在设计风速31.6 m/s条件下，主梁位移响应均方根值及平均值分别列于表3所示。从测试结果可以看出，对于成桥态主梁跨中位置，斜交风对主梁抖振响应影响不明显，仅在30毅风向角下有显著降低。对于1/4跨，正交风下主梁竖向抖振响应显著大于斜交风下的值，但横向和扭转与斜交风下的值相当。在最大单悬臂施工状态下，15毅风向角显著增大了跨中和1/4跨主梁的横向抖振位移，但竖向抖振位移和扭转抖振位移则是正交风下的值大于斜交风下的值，因此施工时应防止过大的抖振位移可能引起的安全问题，如桥上施工机具在大风天气下的有效固定。

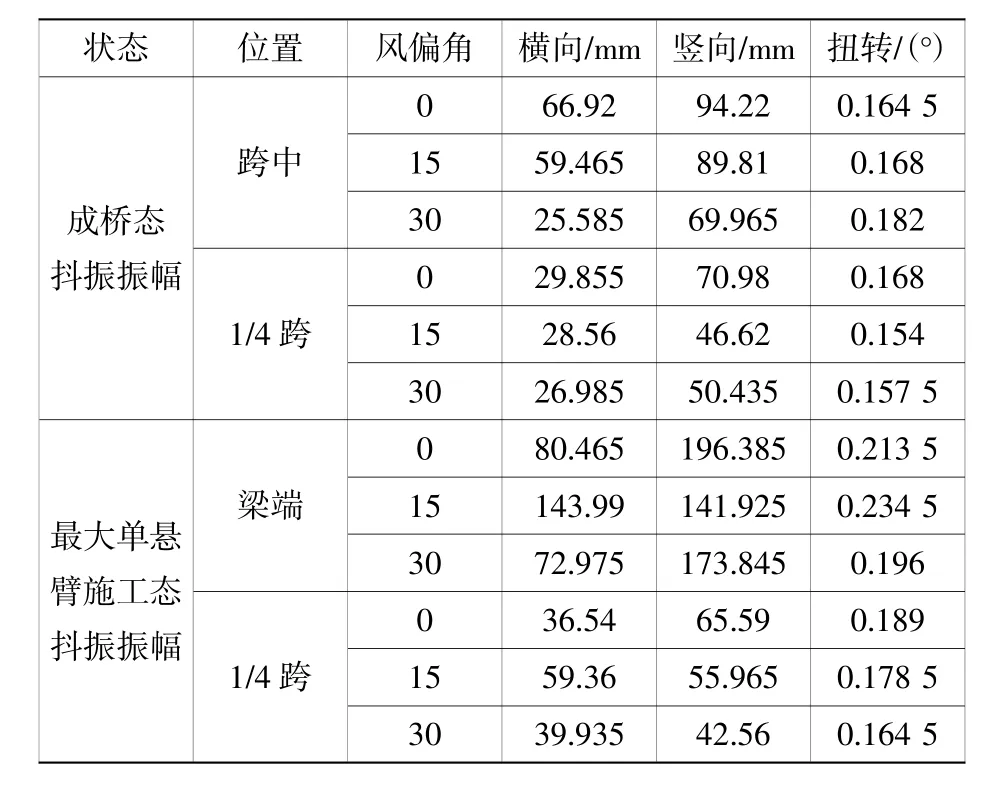
表3 设计风速下主梁的抖振最大位移响应Table 3 The largest buffeting displacement of the girders under design wind speed

根据全桥气弹模型抖振试验所得到成桥状态在设计基准风速下的抖振响应位移，采用随机振动中的SRSS法（平方和开方法），结合有限元计算结果，可反演得到结构的抖振内力。表4为成桥态主梁不同位置处的抖振内力。从表中可以看出，横桥向剪力显著大于竖向剪力，且两个桥塔处主梁的剪力显著大于主跨的主梁，因此横向支座设计时需要充分考虑抖振内力的影响；百年静风荷载计算显示，桥塔处抗风支座受力达2 200 kN，而高塔处横桥向抖振剪力达727.82 kN，因此将桥塔处主梁抗风支座的吨位定位3 000 kN，并增加了主梁和支座交接处的局部加强设计。需要说明的是，尽管采用了高低塔结构，但两个塔处由主梁传递的抖振内力并没有显著的差异，这在抗风设计上需要重视。此外，由于斜交风作用下，成桥态主梁抖振位移小于正交风下的值，因此抖振内力也小于正交风下的值，不用单独考虑。

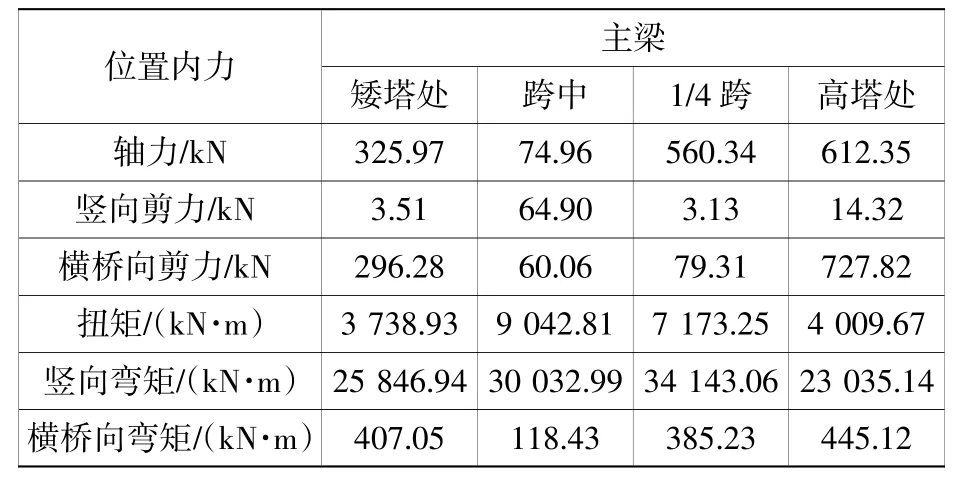
表4 设计风速下成桥态主梁的最大抖振内力Table4 The largest buffeting forceof the girders of the completed bridge condition under design wind speed

4 结语

1）无论是成桥状态还是最大单悬臂施工状态，中跨合龙位置（非主跨跨中位置）或悬臂端位置主梁的抖振响应显著大于1/4跨，表明主梁在自然风作用下的抖振响应均受到第一阶对称振型的显著影响。

2）不同风向角下的抖振位移响应结果表明，对于成桥状态，斜交风对于抖振响应的影响不明显，但在最大单悬臂施工状态，15毅斜交风将会引起横向位移的显著增大，在施工过程中需要加以防范。

3）对于500 m主跨量级的大跨度斜拉桥，由于成桥态斜交风下的抖振响应小于正交风下的抖振响应，因此在抗风设计时可以不用单独考虑斜交风的作用。

4）考虑到抖振引起的桥塔处横向剪力较大，达到了静风荷载计算值的33%，因此进行抗风支座选型时，宜计入抖振内力。