基于直方图均衡化的雾天图像增强技术
李雄伟 王秋云,2 杨昊亮
(1甘肃政法学院公安技术学院,甘肃 兰州 730070;2甘肃省证据科学技术研究与应用重点实验室,甘肃 兰州 730070)
人类对计算机视觉系统的依赖来源于可以通过各种视频监控设备采集到高质量的图像。根据2016年《中国环境状况公报》显示,全国受监测的338个地级及以上城市中,仅有84个城市环境空气质量达标,254个城市环境空气质量超标,338个城市发生重度污染2464天次,严重污染784天次,以PM2.5为首要污染物的天数占重度及以上污染天数的80.3%。雾霾天气高发,不仅给人类的身体健康带来隐性威胁,更直接的是对交通运输、室外监控、侦查、导航、遥感遥测等户外视觉系统的影响。因此,研究图像去雾技术,提升户外视觉系统在恶劣天气条件下采集图像的质量,在实践中具有重大的应用价值。
图像去雾技术是通过一定的方法和手段去除图像中雾的干扰,从而得到高质量的图像,以便得到满意的视觉效果并获取更多有效的图像信息[1]。目前的图像去雾技术主要分为两类,基于图像处理的雾天图像增强技术和基于物理模型的雾天图像复原技术。基于图像处理的雾天图像增强技术不深入研究图像退化的原因,仅从图像本身出发,通过对图像的调整达到凸显图像细节,提高图像质量的目的。主要方法有全局直方图均衡化算法[2-3],同态滤波算法[4],小波变换算法[5],Retinex算法[6-7],曲波变化算法[8],基于大气调制传递函数(Atmospherical Modulation Transfer Function,MTF)法[9],局部直方图均衡化算法[10],局部对比度增强算法[11]等。基于物理模型的雾天图像复原技术则是在研究雾天图像的退化原因的基础上,对图像退化过程建立数学模型,通过反演退化过程对图像失真进行补偿,以期获得效果最佳的去雾图像。其主要方法包括基于偏微方程的雾天图像复原[12]、基于深度关系的雾天图像复原[13-14]和基于先验信息的雾天图像复原[15-16]。
随着计算机视觉系统的普及应用和人工智能的发展,图像去雾技术必将成为图像处理领域的研究热点。同时,由于天气条件的随机性与复杂性,探索研究具有较高普适性、鲁棒性和可靠性的去雾算法有着现实和理论的迫切需要。本文在分析雾天图像特点的基础上,探讨直方图均衡化算法在图像去雾方面的实际功效。
1 雾天图像的特点
空气中的微小颗粒在低气压、空气不流动的环境下会聚集在一起,悬浮在空气中,形成雾霾天气。雾霾天气时的光线在照射过程中有了更多的“反射面”,造成光不正常的吸收和散射,减弱人和户外视觉系统的视觉效果。
数字图像在成像过程中,主要依据光照强度来记录并显示图像的色彩、亮度等信息。雾霾天气对光线的吸收和反射都会对光照强度有所影响,从而影响成像设备对光照强度的准确接受,直接导致图像模糊,对比度降低,层次不分明,细节特征不明显,甚至会造成图像颜色的失真。同时,受地形和气流的影响,雾的形状、浓度随时都在变化,导致雾对图像的影响具有随机性和复杂性。
由于影响雾天图像质量的主要原因是大气中微小颗粒的散射作用,雾天图像退化的物理模型可表述为:
其中:I(x)为带雾图像,J(x)为待定清晰图像,A大气光线强,t(x)∈[0,1]透射率;t(x)又被描述为:

其中,β是大气光散射系数,t(x)随景深变化呈指数衰减。这里公式(1)中清晰图像J(x)被t(x)衰减,大气光线强度A由(1-t(x))衰减。只有I(x)已知,而J(x)、t(x)和A均未知。
所以由式(1)分析,图像去雾问题实质是如何有效确定t(x) 和A,从而得到清晰图像J(x)的问题。
2 直方图均衡化算法
在数字图像处理中,直方图主要是指图像的灰度直方图,表示的是数字图像中各级灰度值及其出现频数或频率的关系的函数。灰度直方图反映了一幅图像中灰度值的概率统计特征,通过概率变换即可改变灰度分布,从而突出图像中所需要的特征量[17]。图像的灰度直方图是一维离散函数,表示为:
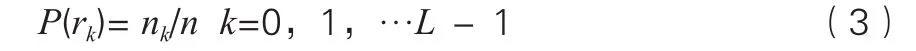
其中,n为图像像素总数,rk表示第k个灰度级,nk表示图像中灰度级rk出现的像素的个数,P(rk)表示灰度级rk出现的概率。
直方图均衡化(Histogram Equalization,HE),是将一已知灰度概率密度分布的图像经过某种变换,变成一幅具有均匀灰度概率密度分布的新图像。直方图均衡化可以改善因为动态范围偏小而造成的图像质量低下问题,同时能够使图像的信息熵最大,这样变换后的图像信息量也就最大,看起来也能够更为清晰。
直方图均衡化的计算过程如下:
(1)统计原始图像、变换后图像的灰度级:i、j=0,1,···,L−1,其中,L代表图像的灰度级数。
(2)计算原始图像中各个灰度级像素的个数ni。
(3)计算原始图像的直方图。

式中,n为原始图像中总的像素个数。(4)计算累积直方图分布。

(5)利用灰度变换函数,采取四舍五入取证的方法,计算变换后图像的灰度值。

(6)确定图像的灰度变换关系:f(m,n)=i,并将原始图像的灰度值初始化g(m,n)=j。
(7)统计变换后图像中各灰度级像素个数nj.。
(8)计算变换后图像的灰度直方图。

直方图与图像的直观视觉效果有对应关系。从上述步骤可以看出,直方图均衡化主要是通过灰度变换函数,将原始图像的直方图变换为均匀分布的形式,从而提高图像的整体视觉效果。
3 实验结果与分析
本文以Matlab 2017b为实验操作平台,将雾天图片通过直方图均衡化进行处理,比较处理后图片与原始图片的均值、标准差、对比度及信息熵,验证直方图均衡化算法在图像去雾中的实际效果。图1为实验效果图,从视觉效果看,经过直方图均衡化处理后的图像亮度明显提升,层次丰富,对比度增强,图像细节特征明显。图2为图像的直方图,经过直方图均衡化后的图像,其灰度值较均匀的分布于[0-255]区间,图像的视觉效果更好。

图1 实验效果图

图2 图像直方图
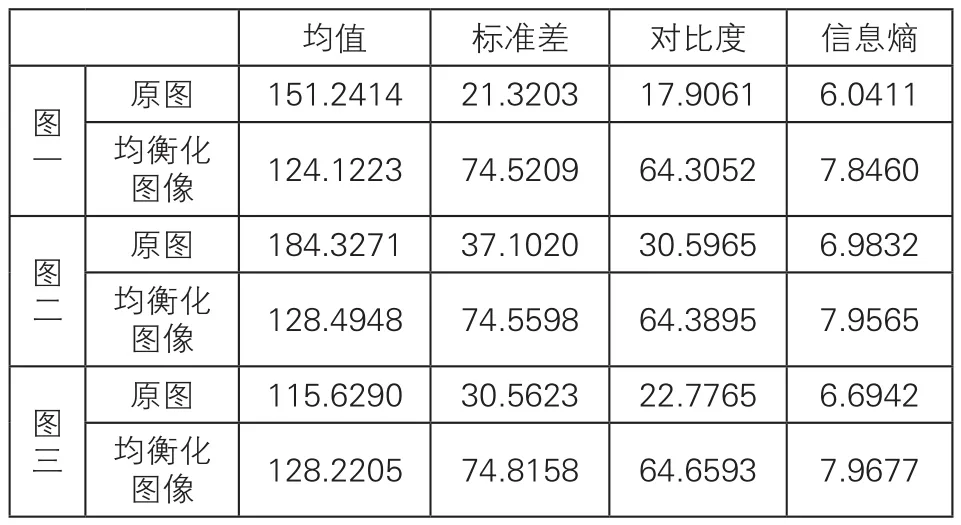
表1 实验数据对比
从表1的实验数据中可以看出,本文所用均衡化处理之后的图像,其均值都在中间值128附近,表明图像的亮度分布更均匀;其标准差、对比度以及信息熵都较原图大,表明均衡化后的图像层次更丰富、清晰,所包含的信息量更大,图像细节更多。
4 结语
通过对实验结果的比较和分析可以得出,直方图均衡化算法对雾天图像具有较好的处理效果,处理后的图像层次丰富,细节和边缘特征明显,尤其是对薄雾图像和简单场景图像,去雾效果更佳。但是,直方图均衡化算法没有考虑雾天图像所包含的复杂景深信息,在计算时不能自适应进行区分,容易出现颜色失真等现象,这点将在以后的研究中加以改进和完善。

