基于自适应子带谱熵和短时平均幅度的心音端点检测∗

吴云飞 李海霞

（宿迁学院信息工程学院 宿迁 223800）

1 引言

心音是心脏节律的外在表现，医学上可以通过监听心音实现对心脏健康状况的分析。每一心动周期可产生四个心音，在正常情况下，心音一般只包含第一心音（S1）和第二心音（S2），除S1、S2之外的心音称为额外心音；而当心瓣膜发生病变时，瓣膜会出现异常的振动及血流的改变，从而产生异常的心音，称心杂音。心杂音可与正常心音分开或相连续，亦可完全覆盖正常心音，因此在心脏病诊断中占有极其重要的地位［1］。

端点检测技术常用于语音信号的分析与识别，噪声环境下的语音端点检测一直是音频信号分析的热点［2］。由于心音信号中心杂音成分的存在，使用滤噪或高门限的端点检测会导致游离于心音外的杂音被当作噪声忽视，而使用低门限的端点检测则会增加误检率。

鲁远耀等提出了利用小波阈值去噪实现强噪下的端点检测技术［3］，但去噪的同时会造成心杂音成分的丢失，不适用于心音领域。路青起等提出了双门限的方法［4］对声纹进行分级，但过于依赖门限的手动设置，同一门限标准难以适用在不同类别的心音中。徐大为等利用有限状态自动机［5］，避免了单一端点检测算法的缺陷，但心音和心杂音往往连续出现，算法要求对心音的状态设定相对复杂。

综上，目前的端点检测技术，已经不能适用于需要利用心杂音进行诊断的情况。因此，本文提出了一种能够有效区分心音和心杂音的心音信号的端点检测方法。

2 端点检测

在端点检测算法中，频域参数的抗噪性一般优于时域参数，但当噪声与语音信号具有类似的变换域特征时会使方法失效。有效的端点检测算法必须具有判决准则能自适应不同的语音信号、在噪声情况下对端点判决的正确率高等特点［6］。所以本文结合频域的自适应子带谱熵算法和时域下的短时平均幅度算法。在频域设置具备自适应性的高门限判决条件，在时域设置固定的低门限判决，实现对心音成分和独立于心音外的心杂音成分的检测。

2.1 自适应子带谱熵

信息熵是为解决对信息的量化度量问题而提出的参数，Jia-lin Shen等提出了基于谱熵的端点检测算法，并表明谱熵算法的性能明显优于短时能量等时域方法［7］。

下式是信号经过分帧及傅里叶变换后的谱熵计算公式：

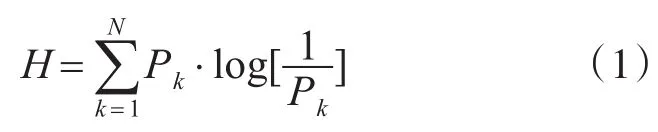
其中N是帧长，Pk为频域分量k的概率密度。

谱熵只依赖于功率谱能量的变化，而不依赖谱的能量，具有一定的鲁棒性。但在信号存在噪声或杂音的情况下，谱熵算法在单个功率点上的幅度易受到噪声影响而导致端点检测的性能明显下降。因此，Bing-Fei Wu［8］等提出的自适应子带谱熵算法，把一帧分成若干个子带，利用归一化最小带能量参数（NMinBE）［9］自适应的选择子带，确定频带的数量。

E（l，m）是第m帧的第l子带的功率谱能量，则归一化最小带能量为

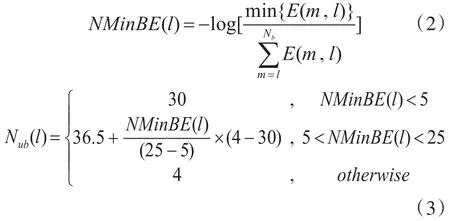
则最终的自适应子带谱熵公式如下：

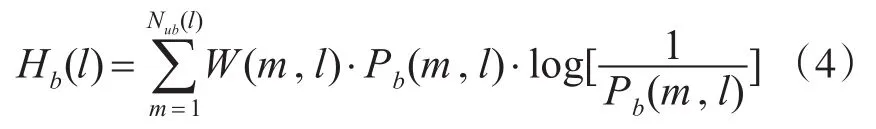
其中的W(m，l)是m及（m±1）三帧的方差，在公式中做加权因子，但在实际应用中，加权后的性能并不优于加权前，故在本文中将W(m，l)设为1。

2.2 短时平均幅值

在心音中，病理性的杂音是心音分析中的重要部分，需要选取合适的处理方法，对除心音外的心杂音成分进行标记。

短时平均幅值在背景噪声增加或者变化的情况下，它的漏检和误检率会比较高［10］，而其对幅度的阈值难以设定，自适应性较差［11］，在低信噪比的情况下不能有效地进行语音端点检测。但本文利用短时平均幅值，对其设定一个较低门限阈值，使其能够对所有心音有效成分的检测，降低了其可能出现的漏检率，且检测方法简单，容易实现。

平均幅值M计算公式如下，其中n是帧长。

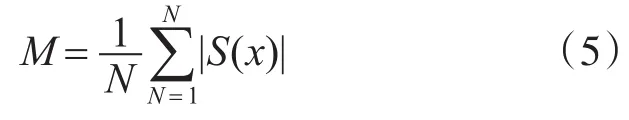
3 算法实现

由于心音信号幅值小，变化多，在对心音信号进行分析前，需进行预处理。首先使用归一化来归纳统一样本，使其幅值在（-1，1）之间，保证设定阈值的可靠性。再通过预加重来提升信号的高频部分，使信号的频谱变得平滑，保持在低频到高频的整个频带中，能用同样的信噪比求频谱［12］。最后利用海明窗对信号分帧，改善截断导致的频率泄露。

图1和图2分别是对一例正常心音的未加重和加重的情况下谱熵（SE）和子带谱熵（ABSE）曲线。

对比图1（b）和图2（b）可以看出加重处理后SE的性能得到了明显改善，基本实现了端点检测的功能，证明了加重处理的必要性。

图1 未加重正常心音的SE与ABSE曲线

图2（b）中加重后的SE性能与图1（c）中未经加重处理后求得的ABSE近似。而在图2（c）中曲线平滑，端点明确，证明了经加重的ABSE使端点检测性能达到最优。

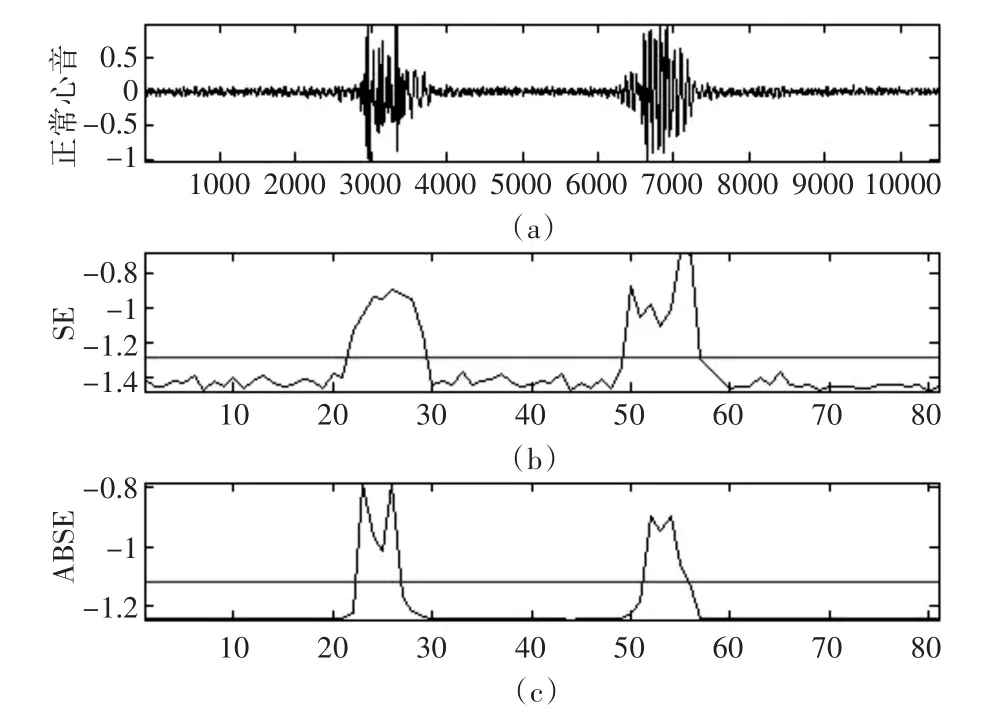
图2 加重正常心音的SE与ABSE曲线

图3和图4为一例主动脉关闭不全的异常心音未加重和加重的情况下的SE和ABSE曲线。

由图3（a）可以看出，在主动脉关闭不全的心音信号中存在大量心杂音，心音成分S1、S2近乎淹没在杂音中，但仍然存在。

图3 未加重异常心音的SE与ABSE曲线

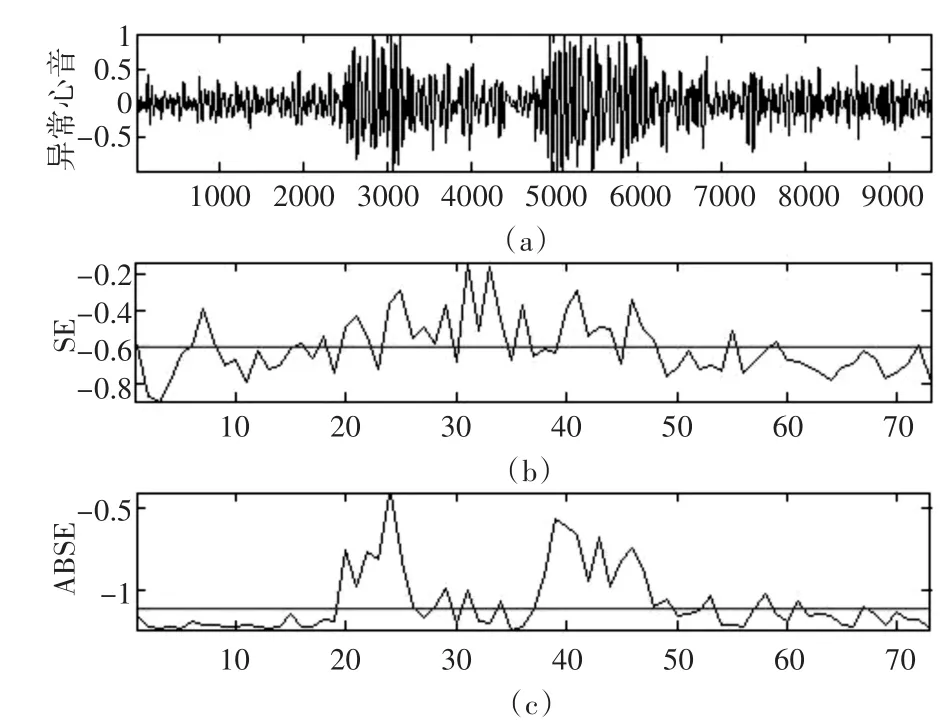
图4 加重异常心音的SE与ABSE曲线

对比图2（b）和图4（b），可以看出，SE在心杂音的情况下即使经过加重仍然失效，证明了SE难以适用于复杂的心音端点检测。

对比图 4（c）与图 3（b）、图3（c）、图 4（b），未经加重处理SE与ABSE以及加重处理后的SE均失效；而加重处理后ABSE曲线较为准确地反应了信号的音区，其阈值线也较好地将心音成分和其他杂音分隔，表现了算法的抗噪性和自适应性，能够用于较为复杂的异常心音的端点检测。

图5（a）是一例二尖瓣狭窄类型的心音，图5（b）是对其进行自适应子带谱熵的端点检测，图5（c）是对其进行短时平均幅度的端点检测。当利用短时平均幅度检测到的有效音覆盖ABSE的有效音，且端点距离较近时，将其视为心音，其余部分视为心杂音。结合两种算法得到最终端点检测结果如图6，其中A、D部分为心音段，B、C部分为心杂音段。

图5 二尖瓣狭窄类型心音的频域与时域分析

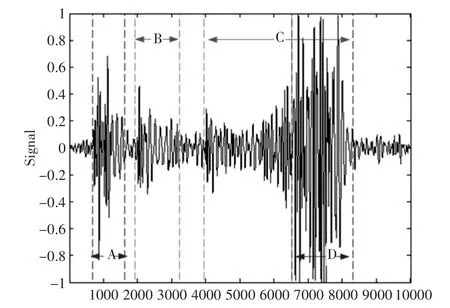
图6 二尖瓣狭窄类型心音的端点检测

为验证方法的有效性和适用性，本文又分别对一例主动脉关闭不全（图7和图8）和动脉导管未闭的异常心音（图9和图10）进行了端点检测。

图7（c）的检测结果及心音有效成分对应图8中的A部分。B、C部分是心音成分；在A部分内除B、C外都为心杂音成分。图10中B部分心音成分，C和除B外的A部分为心杂音成分。

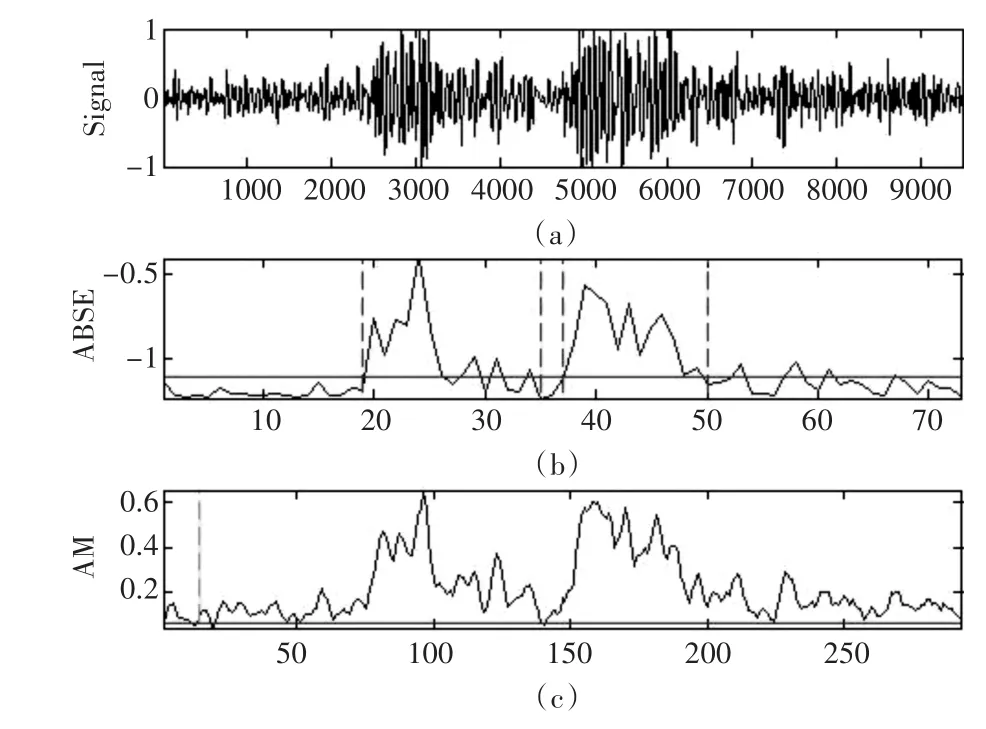
图7 主动脉关闭不全心音的频域与时域分析

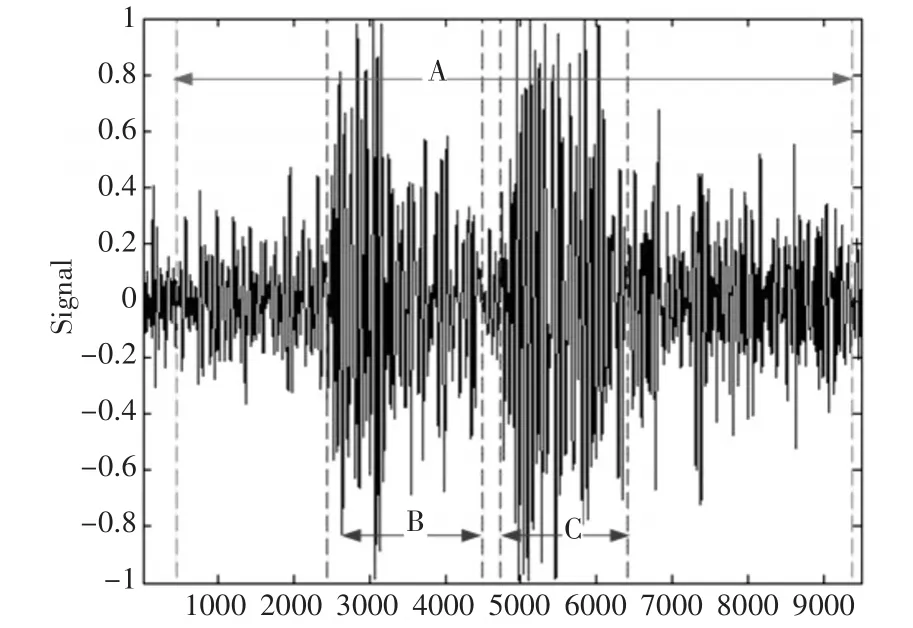
图8 主动脉关闭不全心音的端点检测

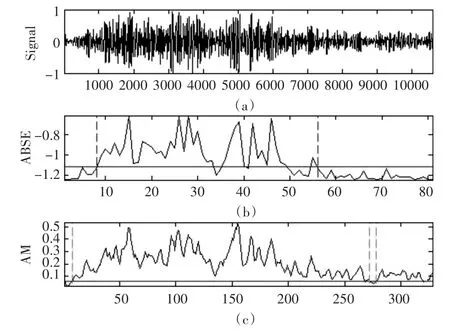
图9 动脉导管未闭心音的频域与时域分析

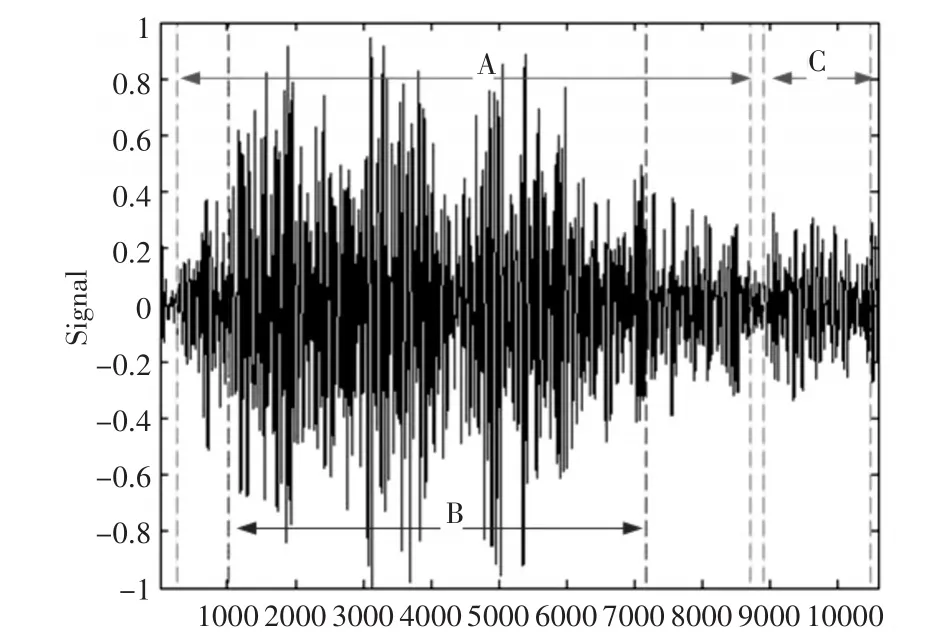
图10 动脉导管未闭心音的端点检测

4 结语

本文结合了频域下的自适应子带谱熵和时域下的短时平均幅值，实现了对心音的端点检测，利用自适应子带谱熵的高门限减少了一般端点检测在心杂音情况下可能的误检，还通过短时平均幅度算法检测出心音的全部有效成分，避免了对心杂音的漏检。通过对三例异常心音的端点检测，证明该算法具有自适应性，能够在多种类型的复杂心音条件下进行有效的检测，可以用于心音信号进一步的分析和识别。但算法对于覆盖在心音上的心杂音成分只能对其位置进行标记，还无法做到正确辨识，这将是下一步工作的重点。