基于状态空间的阻抗分析法在次同步振荡中的应用

赵书强, 李 忍, 高本锋

(新能源电力系统国家重点实验室, 华北电力大学, 河北省保定市 071003)

0 引言

随着新能源大规模接入,传统电力系统的次同步振荡(sub synchronous oscillation,SSO)问题呈现出新的复杂形态,日益成为制约新能源可靠消纳的瓶颈[1-8]。SSO的线性化分析方法可大致分为两大类:基于状态空间模型(state space models,SSM)的时域类分析法和基于阻抗模型(impedance models,IM)的频域类分析法[9]。虽然上述2类方法从不同的角度对电力系统进行建模,但基本数学原理均源于电力系统两大约束:元件约束和拓扑约束。因此,时域类分析方法和频率类分析方法可以相互转换。

基于SSM的时域类分析方法,由于在每次计算系统特征值的时候,都需要对整个系统进行建模,这对于系统结构变化不大的发输电系统,适用性较高。但是,对于一些结构频繁变化的系统,比如源—网—荷系统,尤其是含新能源电源的系统,负荷波动或者新能源电源启停,将会导致待研系统频繁重新建模,大大增加了建模的工作量[9-11]。

阻抗分析法由于物理概念明晰[12-14],适用于理论分析与实验测试相结合的情况,近年来在分布式电源稳定性分析方面,得到了广泛应用[15-22]。文献[14-15]基于阻抗法研究了电网阻抗对光伏逆变器稳定运行的影响。文献[16-17]基于阻抗法对直流输电系统进行建模,研究了海上风电经高压直流输电(HVDC)系统的稳定性。文献[18]基于阻抗分析法,研究了双馈风电机组经串联补偿并网SSO的机理及关键影响因素。文献[19-21]基于广义奈奎斯特判据,提出了三相交流系统阻抗分析法的判据。

然而,阻抗分析法最开始用于处理直流系统这类单输入单输出系统,后来发展到处理三相变流器并网稳定性问题[23]。阻抗分析法的建模方法,多适用于对非线性电路的建模,难以对非线性机械系统进行建模。因此该方法专注于电力电子装备的研究,鲜有涉及传统火电机组。传统阻抗扫描法仅能计及火电机组发电机定子的电气特性[2-4,11],无法对轴系的机械特性进行建模,而轴系动态特性对SSO的研究具有重要影响。

本文提出了一种基于状态空间的阻抗分析法(IMBSM),其包括建模方法和新判据2部分。IMBSM建模方法将机械、控制及电气系统以状态空间的形式统一建模,遴选出控制和机械系统耦合到电气系统的动态特性,刻画到阻抗/导纳函数的电气特征中,实现了电力系统中非电气元件和电气元件的电气化建模。新判据基于源网子系统的视在谐振点,计算系统的物理谐振点,避免了奈氏判据所需的复杂矩阵求逆或相乘运算。此外,基于导纳函数矩阵,有利于多源并网系统电源子系统的等效计算。

1 IMBSM的建模方法

1)状态空间与传递函数

状态空间是现代控制理论的基础,其不仅能反映系统内部状态,而且能揭示系统内部状态与外部的输入和输出变量的联系,所以状态空间表达方式是对系统的一种完全描述。典型的状态空间模型为:

(1)

式中:x=[x1,x2,…,xn]T为n维状态变量;u=[u1,u2,…,um]T为m维输入量;y=[y1,y2,…,yr]T为r维输出量;A,B,C,D分别为状态矩阵、输入矩阵、输出矩阵、直接传递矩阵。

可将式(1)转换为传递函数模型,只需满足式(2)，即

(2)

式中:H(s)为第r行m列的传递函数矩阵;I为单位矩阵。

在dq轴同步旋转坐标系下,建立电力系统及元件的状态空间模型。当输入量选择电压u=[ud,uq]T,输出量选择电流y=[id,iq]T时,可将此状态空间转换为传递函数。由式(2)可知,此传递函数即导纳函数矩阵,可表示为:

(3)

(4)

为便于叙述,本文称Ydd和Yqq为主对角线元素,Ydq和Yqd为副对角线元素,后文与此对应。此外,当输入量选择电流u=[id,iq]T,输出量选择电压y=[ud,uq]T时,可将此时的状态空间转换为阻抗函数矩阵，即

(5)

(6)

2)阻抗分析法的基本原理

阻抗分析法的基本原理如附录A图A1所示,基于戴维南等效定理,将待研系统等效成电源与电网两部分,电源输出阻抗为Zs,电网输入阻抗为Zg。通过分析Zs/Zg是否满足奈奎斯特稳定性判据,进而判定串联系统的稳定性。当Zs和Zg为矩阵时,稳定性判据需采用广义奈奎斯特稳定性判据[12]。

上述阻抗分析法,其稳定性分析的核心在于求解电源、电网子系统的谐振频率,以及谐振点下的相角裕度;提高稳定性的措施,则可采用提高相角裕度和避开谐振频率等方法。

3)IMBSM建模方法

理论上,基于状态空间,既可建立源、网子系统的阻抗函数模型,也可建立其导纳函数模型,如式(3)至式(6)所示。但是,电力系统大多数元件都含有电感,在对其进行状态空间建模时,电感电流常作为状态变量。以基尔霍夫电压方程为拓扑约束,输入量被限定为电压,输出量则限定为电流。由式(3)和式(4)可知,基于状态空间建立的传递函数模型均为导纳函数矩阵。IMBSM建模方法的流程图见附录A图A2。

IMBSM建模方法对电源和电网子系统状态空间的建模与现有阻抗分析法具有明显不同,后文会详细介绍。此外,现有阻抗分析法基于奈奎斯特稳定性判据求解谐振点频率,当系统较为复杂时,复频域矩阵运算可能导致无解[23-24],而IMBSM的新判据将有助于解决这一问题。

2 适用于IMBSM的新判据

现有阻抗分析法,以奈氏判据为判稳依据,涉及阻抗函数矩阵运算(相乘/求逆),当源网子系统阻抗/导纳函数较为复杂时,复数矩阵运算存在较大误差,甚至可能导致无解。为使IMBSM可应用于复杂系统,本文提出了一种以导纳函数矩阵为运算单元,可免除复数矩阵运算的新判据。

其研究思路为:首先基于简单系统,研究不同坐标系下串联谐振在导纳函数波特图上的表现特征;定义表征串联谐振的视在谐振点;推导视在谐振点与物理谐振点的数学关系。

2.1 不同坐标系下串联谐振

在abc三相静止坐标系(后文简称abc坐标系)中,当三相平衡时,三相电路可由单相表示,后文中abc三相电气量均用a相表示,下标a省略。

设串联RLC线路电感为L,电容为C,线路电阻为R,工频角速度为ωb(本文采用120π)。如式(7)至式(9)所示,忽略电阻的影响,串联谐振点既是阻抗函数ZLC(ω)的零点,也是导纳函数YLC(ω)的极点，即

(7)

(8)

(9)

式中:k为串补度，此处取k=50%;ωr为谐振角频率。

本文记abc坐标下的串联谐振点为物理谐振点。如附录A图A3所示,在物理谐振点处,电感和电容的阻抗函数波特图满足幅值相交、相位相差180°,此交点也为ZLC(ω)的零点。

同理,在dq轴旋转坐标系(后文简称dq坐标系)中,当abc三相电路对称时,忽略零轴量。由派克变换,RLC线路电感和电容阻抗/导纳函数为2×2阶矩阵[11]，即

(10)

(11)

(12)

由式(10)和式(12)可得,串联LC的阻抗函数矩阵ZLC(s)为:

(13)

对ZLC(s)求逆,得到串联LC的导纳函数矩阵为:

YLC(s)=

(14)

求式(13)和式(14)的零点及式(14)的极点(忽略工频极点),结果为:

(15)

式中:ωzero和ωpole分别为零点和极点。

ωzero和ωpole具有以下特点。

1)零极点中均包含了串补度k的信息,因此零点和极点都是串联谐振在dq坐标系下的特征,本文称其为特征谐振点。

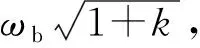
3)YLC(s)所有元素具有相同的极点,同时含有次同步频率和超同步频率的极点。

特征值分析可以得到RLC线路的振荡模式,其模态频率工频互补[2-4,11],对应YLC(s)的极点。但是,对于ZLC(s)和YLC(s)的零点信息,特征值分析法无法获取。因此,IMBSM的建模方法比特征值法获得的信息更多。

2.2 视在谐振点

abc坐标系中,串联谐振点(物理谐振点)为阻抗函数的零点,同时也为导纳函数的极点。上一节的分析结果表明,这一结论在dq轴坐标系下不成立。但是,串联谐振点在导纳函数波特图上呈现谐振的“视在”特征,本文称其为视在谐振点。

首先,给出视在谐振点的定义。定义1:假设dq坐标系下,某三相平衡交流系统由有2个子系统A和B串联而成,设系统A和B的导纳函数矩阵分别为YA(s)和YB(s);定义系统的视在谐振点YA(s)和YB(s)在同一波特图上幅值相交,相位相差n×180°(n为奇数)点处的角频率;定义Yplus(s)为系统的视在导纳,且有Yplus(s)=YA(s)+YB(s),则视在谐振点等于视在导纳的零点。

1)LC串联谐振

首先,以最简单的LC串联系统为例,分析串联谐振点在波特图上的特征,如图1所示。

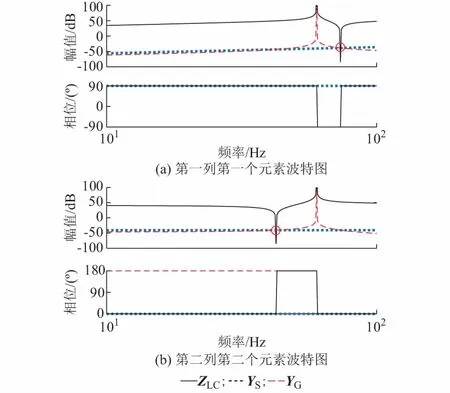
图1 LC串联系统源、网子系统的导纳函数波特图Fig.1 Bode diagram of subsystem for source and grid in LC series system

源、网子系统分别用YS和YG表示。图1表示LC串联系统导纳函数的波特图(只给出第一列元素的波特图)。由图1可知,YS和YG的导纳函数在波特图上存在幅值交点,且此交点下,相位相差180°。图中红色标出交点为视在谐振点。

图1还给出了LC串联系统总阻抗ZLC(s)的波特图,视在谐振点具有谐振点的“视在”特性,但是其与ZLC(s)的特征谐振点(零点)物理意义不同,具体分析如下。

式(16)表示LC串联系统的视在导纳Yplus(s),式(18)中k与式(9)相同,表示RLC线路的串补度(k=50%)。根据定义1,其由YS(s)和YG(s)相加而得。对比式(13)可知,二者虽然具有完全相同的零极点(图1中二者重合),但是Yplus(s)和ZLC(s)并不相等。

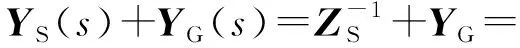
(16)

(17)

(18)

2)LLC串联谐振

进一步,分析LLC串联系统。当电网阻抗与电源阻抗分开建模时,如图2所示的LLC串联系统,电源子系统用YS1表示,电网子系统用YG1串联表示(串补度k=50%)。

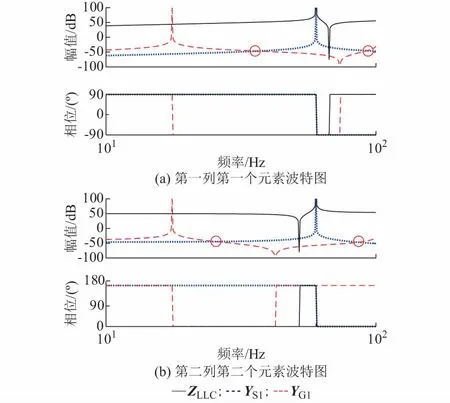
图2 LLC串联系统源、网子系统的导纳函数波特图Fig.2 Bode diagram of subsystem for source and grid in LLC series system

图2子系统的导纳函数波特图,同时给出了LLC串联系统总阻抗ZLLC(s)的波特图。由图2可知,LLC串联系统存在4个视在谐振点,如图中红色标出的交点所示。不同于图1,图2中的视在谐振点与系统阻抗ZLLC(s)的零点不相等,但二者存在一定的关联,具体见后文推导过程。

由以上分析可知,在LC串联系统和LLC串联系统中,串联谐振使导纳函数波特图上产生视在谐振点。因此,本文所提新判据便基于此特征,由导纳函数波特图上的视在谐振点,计算串联系统谐振频率。上述视在谐振点的寻找方法与现有阻抗分析法寻找谐振点的方法相同,但是二者存在一定的差别。本文中的4个视在谐振点方可计算得到一个物理谐振点,并且该物理谐振点无法在波特图上直接读取,而现有阻抗分析法可以直接读取物理谐振点。

2.3 串联谐振点计算

下面介绍由视在谐振点,计算串联谐振频率的方法,以LLC串联系统为例。

设YS子系统的等效电感为L1,LC子系统的串补度为k,LLC串联系统物理谐振角频率为ωrLLC,记L1与L之比为源网阻抗比n,则有:

(19)

仍设Yplus(s)=YS1(s)+YG1(s),则有

(20)

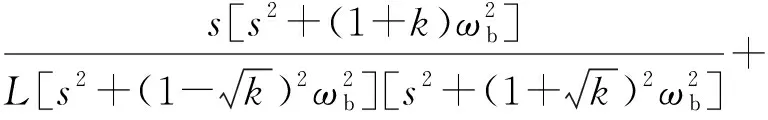
(21)

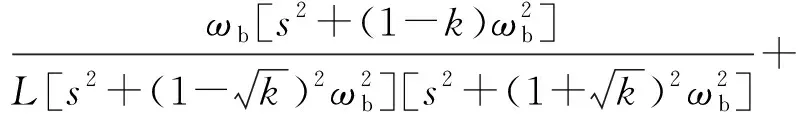
(22)

式中:Ydd(s)和Yqd(s)分别为Yplus(s)的主对角线元素和副对角线元素,由于主对角线元素相同,副对角元素互为相反数。

Yplus(s)的零点由Ydd(s)=0,Yqd(s)=0的解组成。设Yplus(s)的零点分别为ωr1,ωr2,ωr3,ωr4,则解得:

(23)

(24)

ωr1,ωr2,ωr3,ωr4即为LLC串联谐振系统的视在谐振点,其结果与图2吻合。由视在谐振点计算物理谐振频率ωrLLC，即

(25)

(26)

式中:ωsum为Yplus(s)主对角线元素的零点平方和与副对角线元素的零点平方和之和;ωsub为Yplus(s)主对角线元素的零点平方和与副对角线元素的零点平方和之差。

同理,对于LC串联系统,同样存在与式(26)类似的关系,即

(27)

此时,ωr1=ωr2,ωr3=ωr4,ωsub同式(25)。因此,图1中,视在谐振点的实际个数依然是4个,LC串联系统可以看做是LLC串联系统的一个特例。

LC串联系统与LLC型串联系统建模的区别在于电网子系统的建模,当电网子系统中电感已知时,可以将其等效并入电源子系统,那么电网子系统只包含电容,此时系统可划分为LC串联系统;当电网子系统中电感参数由于数据不足或者其他原因导致求解困难时,此时电网子系统必然包含了电感和电容,则待研系统只能划分为LLC串联系统。

由上述结果可知,视在谐振点与物理谐振点在数学上存在等价关系,通过波特图上直观的视在谐振点,可以求出系统的物理谐振点。此即本文所提串联谐振判据的理论依据。

新判据避免了奈氏判据所需的复数矩阵求逆或相乘运算;以导纳函数矩阵为运算单元,当电源系统包含多个发电单元时,电源子系统的等效计算仅为各发单元的代数相加,再次简化了阻抗函数矩阵的求逆运算。

3 IMBSM用于SSO

为验证IMBSM建模方法及新判据的准确性,同时探究二者用于SSO分析的可行性,选取SSO第一标准模型(SSR FBM)作为算例。

3.1 基于IMBSM的火电机组建模

根据IMBSM的建模方法,将SSR FBM分成电源和电网两部分,分别计算源、网部分的导纳函数矩阵。因此,状态空间建模需采用分块建模的方法,依次建立电源和电网部分的状态空间模型,具体建模方法见文献[24]。

附录A图A4为SSR FBM的示意图,包含了电源子系统和电网子系统。汽轮机、轴系、发电机、调速器(图中未画出)、励磁机组成电源部分模型;升压变和RLC输电线路组成电网部分模型。

图3给出了火电机组导纳函数矩阵第一列元素(Ydd，Yqd)的波特图。对比图2中YS1子系统的导纳函数波特图可知,火电机组导纳函数波特图,总体呈现电感特性,但在次同步频率下,存在4处“峰谷点”。此外,对于新能源机组,以双馈风电机组(DFIG)、永磁直驱风电组及光伏为例,其整体也呈现电感特性[5,18,22]。

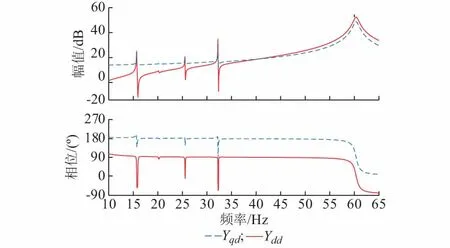
图3 火电机组导纳函数波特图(第一列)Fig.3 Bode diagram of admittance matrix belonging to thermal power units (the first line)

SSR FBM火电机组轴系为六质量块模型,含有5个扭振模式(torsional mode,TM),其频率由高到低分别是47.46,32.32,25.57,20.22,15.78 Hz。将这5个模式依频率由高到低分别命名为TM5至TM1。图3中,4个“峰谷点”分别对应TM1至TM4,TM5未能显现在火电机组导纳函数中,理由如下。

文献[2]给出了TM5至TM1的参与因子分析结果,TM5(47.46 Hz)主要由高压缸(HP)和中压缸(IP)主导,电气系统几乎不参与该扭振模式,即TM5模式中机电耦合较弱。因此,从火电机组导纳函数的波特图上,可以较为直观地观察机电耦合度的大小。

在dq轴坐标系下建立火电机组图形化状态空间模型时,电气、机械及控制系统,均以状态空间的形式建立彼此的联系。最终,这种联系通过阻抗/导纳函数的视角,被“观察”到。由此可知,导纳函数遴选出了机械系统耦合到电气系统的动态特性,对于与电气系统不存明显耦合的动态特性,则被“过滤”掉。与基于状态空间的特征值分析法相比,基于状态空间的阻抗分析法,不必求得系统所有振荡模式,因为从导纳函数中“观察”不到的振荡模式已被自动“过滤”。

3.2 基于新判据的振荡频率计算

电源、电网子系统导纳函数的波特图如图4所示,图中Yddgen和Yqdgen表示电源子系统导纳函数;Yddrlc30,Yqdrlc30和Yddrlc50,Yqdrlc50分别表示不同串补度(30%和50%)下电网子系统导纳函数。图4中,电网子系统(RLC)的导纳函数波特图与图2中YG1相近,由于线路电阻的存在,前者波特图在零极点处更为平缓。

图4 新判据下源、网子系统导纳函数的波特图Fig.4 Bode diagram of subsystem for source and grid system under new criterion

图4中,当RLC线路的串补度k分别为30%和50%时,源、网子系统导纳函数在波特图上均出现了视在谐振点。根据定义1对视在谐振点的定义,两种串补度下,Ydd和Yqd各存在2个视在谐振点,如图中红色圈中交点所示。

尽管Ygen在轴系模态频率处存在“峰谷点”,源、网子系统导纳函数幅值交点的个数偏多,但是结合相位相差180°,最终确定的视在谐振点个数依然与理论分析一致。

将图4中视在谐振点放大,拾取角频率,结果如表1所示。

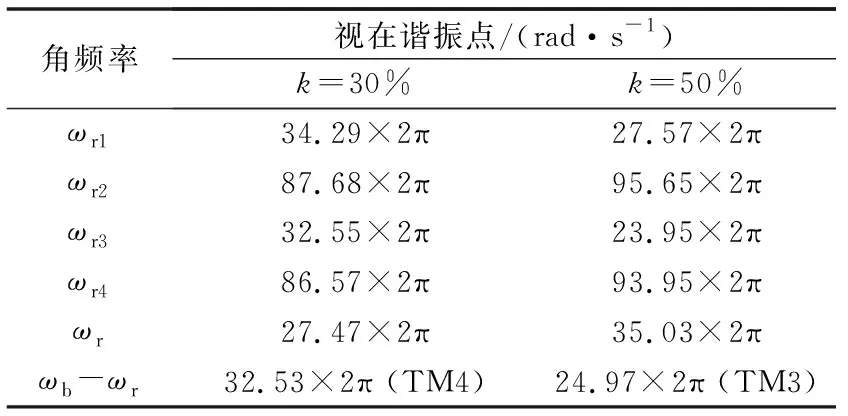
表1 不同串补度下的视在谐振点Table 1 Apparent resonance points at different compensation levels

基于表1中不同串补度下的视在谐振点,由式(23)计算物理谐振频率ωr。由abc坐标系下的物理谐振点计算可能被激发的轴系模态频率ωb-ωr[2]。

串补度为30%时,轴系TM4模态频率与物理谐振频率接近互补而可能被激发;同理,串补度为50%时,轴系TM3模态可能被激发。这一分析结果与文献[2]中特征值计算结果完全吻合。因此,本文所提串联谐振判据,对于SSO振荡频率的计算具有较大的精度,可作为IMBSM的判据,用于复杂系统谐振频率的计算。

鉴于SSR FBM的时域仿真模型已在PSCAD/EMTDC中以example的形式搭建完成,相关的时域仿真结果较多[2],本文不再单独列出时域仿真波形。

3.3 风火打捆经串补送出系统算例

为进一步验证本文方法在电力电子化电力系统中的适用性,在SSR FBM中接入风电,建立风火打捆经串补送出系统(以下简称WTBC系统)的状态空间模型和时域仿真模型。其中风电机组采用DFIG,WTBC系统电气接线示意图如附录A图A5所示,图中PCC表示公共耦合点。

风电机组模型主要包括以下基本单元:风机轴系、异步发电机、转子侧换流器(RSC)、直流电容、网侧换流器(GSC)、电网与GSC接口模型。

风机轴系采用可以计及次同步模式的两质量块模型[5-6];异步电机采用5阶模型(含转子运动方程);RSC和GSC采用功率/电压外环、电流内环的双比例—积分控制,矢量控制均采用电网电压定向。RSC和GSC的控制策略参见文献[5]。

风火打捆系统中,风电场出力100 MW,火电机组出力800 MW。风电场由50台单机容量为2 MW的DFIG机组聚合而成,聚合后的风机参数见文献[5]。系统其余运行参数与SSR FBM相同。

基于上述参数,建立WTBC系统的状态空间模型,计算电源和电网子系统的导纳函数,其中,电源子系统由火电机组和DFIG导纳函数并联而成,电网子系统为串补输电线路。

现有阻抗分析法对于解决复杂电路系统时,其构想为:当电网系统更为复杂时,可以利用基本单元阻抗串并联构建复杂电网系统;当电源系统更为复杂时,可以先计算单一电源详细的线性化阻抗模型,然后聚合成复杂电源系统的阻抗函数[23,25]。

与图4类似,在附录A图A6中,当RLC线路的串补度k分别为30%和50%时,源、网子系统导纳函数在波特图上均出现了视在谐振点(图中曲线不连续是由纵坐标限幅导致)。根据定义1对视在谐振点的定义,两种串补度下,Ydd和Yqd各存在2个视在谐振点。

在附录A图A6中,选中视在谐振点,其对应的横纵坐标数值如图A6所示,将结果整理到附录A表A1中。对比附录A表A1和表1的结果可知,由于DFIG的接入,电气系统的谐振频率发生了变化,则火电机组被激发的扭振模态也将发生改变(调整DFIG控制器参数使DFIG不发生次同步振荡),下文通过时域仿真进行验证。

为验证上述分析结果,基于PSCAD/EMTDC建立WTBC系统的时域仿真模型,不同串补度下线路电流、火电机组被激发模式的扭转转速(标幺值)曲线如附录A图A7所示。如图A7(a)和A7(c)表明,串补度为30%时,c相电流中谐振分量的频率为33 Hz,同时,TM3(25.57 Hz)模式被激发;图A7(a)和(d)表明,串补度为50%时,电流中谐振分量的频率为40 Hz,同时,TM2(20.22 Hz)模式被激发。图A7中快速傅里叶变换分析基于MATLAB powergui tool,截取2～3 s时域仿真数据。

4 结语

本文所做的主要工作和相关结论如下。

1)IMBSM建模方法将机械、控制及电气系统以状态空间的形式统一建模,遴选出控制和机械系统耦合到电气系统的动态特性,刻画到阻抗/导纳函数的电气特征中,实现了电力系统中非电气元件和电气元件的电气化建模。

2)适用于IMBSM的新判据,通过拾取源、网子系统的视在谐振点,计算串联谐振频率,相对于奈氏判据,可免除复数矩阵的运算,有利于IMBSM用于复杂系统。

3)IMBSM不仅包含了系统特征值等关键信息,并且具有比阻抗扫描法更高的精度,同时拓展了现有阻抗分析法的应用范围。

4)采用IMBSM,获取火电机组的精细化导纳函数,对于新能源与常规能源打捆系统稳定性的研究具有重要意义。

此外,本文所提IMBSM对于由串补引起的SSO问题的适用性,已得到验证,但对于直流引起的火电机组轴系扭振以及永磁直驱风电机组经弱交流并网SSO问题,IMBSM是否具有普适性,有待继续深入研究。理论上,若系统存在物理谐振点,则IMBSM便具有适用性,问题的关键是判据的精确性和实用性。使IMBSM适用于直流引起的次同步振荡以及永磁直驱风电机组经弱交流并网SSO问题,进而用于分析新能源与火电打捆系统SSO的研究,是后续重点研究方向。针对论文观点的详细讨论,见附录B。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

本文获得国家自然科学基金资助项目(51507064，51675178)的资助,特此致谢!