无线自组网的自适应同步技术研究

宋晓雪, 魏 路, 林水生

(1. 电子科技大学通信与信息工程学院, 四川 成都 611731; 2. 通信网信息传输与分发技术重点实验室, 河北 石家庄 050811)

0 引 言

无线自组网中节点的频繁移动,网络拓扑的快速变化,导致节点之间通信链路的不稳定[1],使得同步过程中传输的分组碰撞率以及丢包率显著增大,难以将成熟的时间同步算法应用于动态网络中。而高效精确的时间同步是无线自组网的前提[2],确保正常的数据交互和时隙调度,所以时间同步技术是无线自组网的重要研究内容。

在时间同步方面,在给出时钟同步模型的基础上[3],对时钟漂移在同步过程中的影响进行了详细的数值分析[4-5],以及对时钟偏差进行比较精确地估计[6-8]。而在无线自组网中,不同同步算法有不同的特性[9],以较高的同步精度为前提,减少同步过程所需的分组数量是至关重要的[10]。通过减少同步分组的传输量,减少了冗余分组[11],进而提高了同步效率,使得全网同步具备了更快的收敛速度[12]。在动态网络的时间同步中,某一性能得到提升,但对同步分组的传输没有很好地控制[13],也有为了均衡各个性能而只能在两跳的范围内有效工作,网络规模局限性比较大[14]。对网络拓扑的优化策略[15],以时延均衡拓扑概念为基础的时钟同步协议,但算法较为复杂,以及基于接收者-接收者同步方案的能量高效率同步协议[16],可以显著降低通信开销以实现低功耗。以上研究都没有考虑在动态网络中既保证适当的精度又使得同步分组传输数量减少。

本文基于动态无线自组网的特性,通过双向交互同步获得节点间的时延,运用局部加权线性回归对时间戳进行拟合,使得同步算法能够自适应于无线自组网的复杂环境。

1 基本时间同步算法

本文时间同步算法采用分布式与集中式相结合的同步方式[17]。在分布式同步中采用了发送-接收双向交互同步算法[18],以及在集中式同步中采用了洪泛时间同步算法。

1.1 基于发送者-接收者的同步算法

传感器网络时间同步协议(timing-sync protocol for sensor network,TPSN)[19]是典型的基于发送者-接收者的双向同步机制的同步算法。具体报文交互过程如图1所示,节点A是待同步节点,在T1时刻给节点B发送同步请求报文,并把时间戳作为报文消息也发送出去,随后节点B在自己本地时间为T2时刻收到该报文,经过一段时间的处理后,在T3时刻给节点A发送响应报文,同样T2和T3时间戳包含在报文中,在节点A的本地时间为T4时刻时收到响应报文,因此节点A还有用于时间同步的4个时刻信息:

TA(t4)=TB(t3)-θA,B+delayB

(1)

TA(t4)=TB(t3)-θA,B+delayB

(2)

假设A到B,B到A的传播延时相同,可计算出节点A和节点B之间的传输延时:

(3)

图1 TPSN节点的报文交互过程Fig.1 Message exchange process for TPSN

1.2 洪泛时间同步协议

洪泛时间同步协议(flooding time synchronization protocol,FTSP)[20]采用层次结构实现整个网络的时间同步。在层级结构中采用分级的形式进行逐级同步,根节点设置为0级节点,在根节点的一跳邻居节点设置为1级节点,一跳邻居节点的邻居节点设置为2级节点,依次设置节点级别。同步时,级别为i+1的节点与级别为i的节点进行同步,在层级结构网络中的节点都会收到同步报文完成同步然后继续广播同步报文,以让下一级节点完成同步。因此,同步过程可以看成是级别小的节点向级别大的节点逐层扩散的同步方式,最终全网节点达成同步。

如图2所示,节点0为根节点,根节点向外广播同步包,一层节点(1,2,3,4,5,6)收到同步包后根据回归拟合方程进行时间同步,然后通过随机竞争方式抢占信道,接着广播本地同步之后的时间以便二层节点(7,8,9,10,11,12)进行同步。本文算法使用FTSP的广播信息功能以及利用局部加权线性回归的思想,完成所有节点的同步过程。

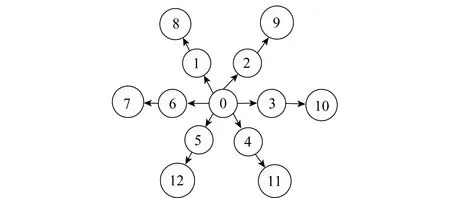
图2 洪泛时间同步模型Fig.2 Synchronization model for FTSP

在FTSP中[21],算法采用一元线性回归对时间漂移率和偏移进行估计和补偿。在线性回归中,对于给定节点的时间戳对(t2,t1),线性回归算法通过选择合适的参数向量θ以最小化flin(θ):

(4)

在一定的样本集中,当采用线性方式拟合数据,若样本集中的数据的自变量和应变量有较好的线性模型时,线性拟合能很好地体现这种关系,若两变量没有明显的线性关系时,线性拟合出的效果会明显出现偏差,得出的结果与实际相差较大,将使得这种线性回归出现严重的欠拟合。

2 局部加权洪泛时间同步算法

2.1 局部加权线性回归

本文采用局部加权线性回归(locally weighted linear regression,LWLR)[22]实现时间戳对的拟合。

LWLR的处理方式如下:选择合适的参数向量θ最小化fLWLR(θ):

(5)

式中,w(i)是对局部数据选择的一种参数[23]。w(i)的数学定义为

(6)

式中,t表示预测的值;t(i)是第i个时间戳样本数据;τ表示该权值代表的衰减程度,τ值越大,该权值衰减得越慢,否则越快,τ也是LWLR时间同步算法中需要考虑的重要参数。式(6)表明，随着t(i)离t越远,权值w(i)越小。

θ=(XTWX)-1XTWY

(7)

得到拟合参数值,其中

2.2 同步过程

本文同步算法采用分布式与集中式结合的同步方式,既避免了分布式同步的复杂,开销较大,且收敛较慢,又克服了集中式同步过分依赖于参考节点,并且交互包的数量较多,存在较大的碰撞率,具体同步过程如图3所示。

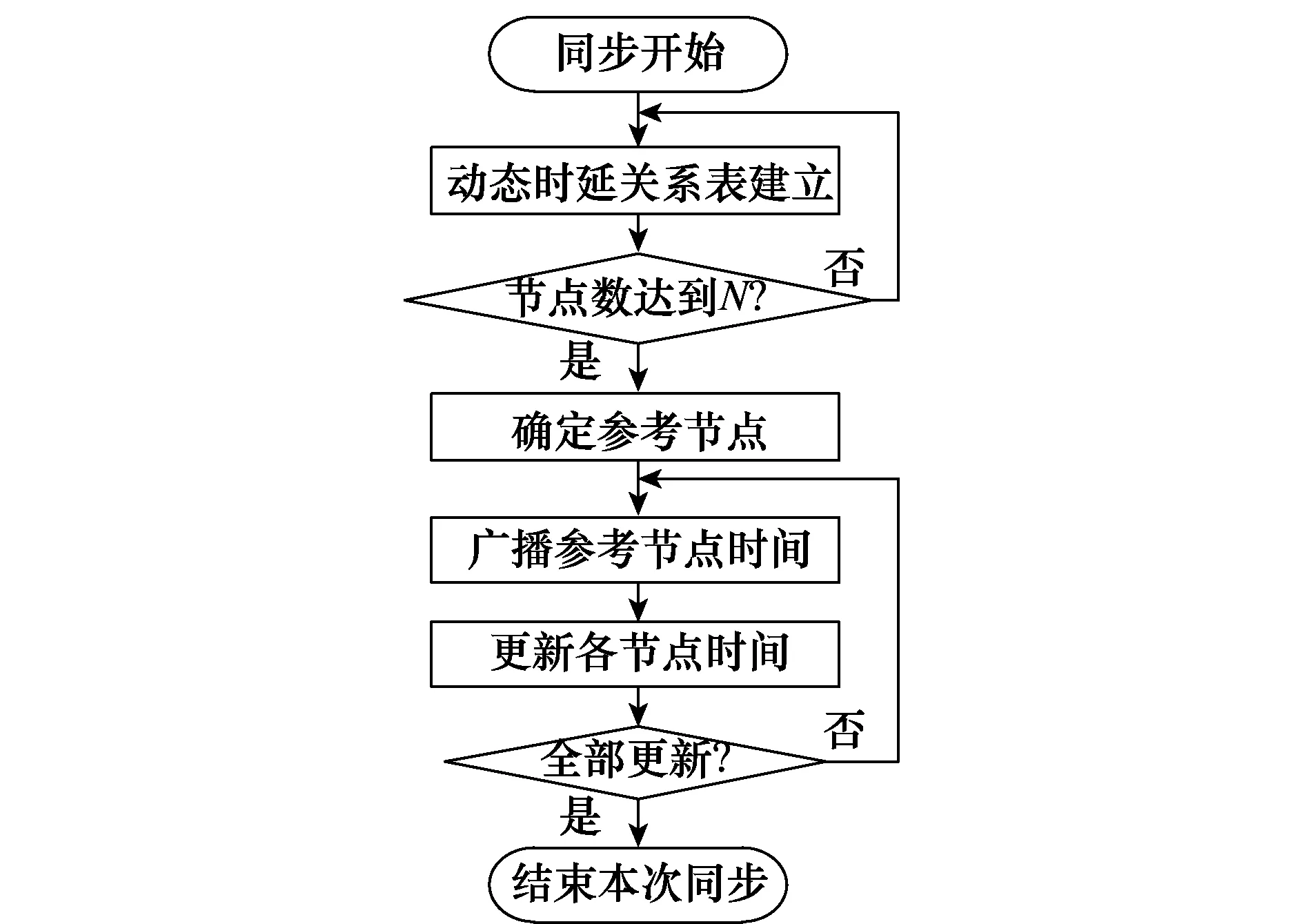
图3 同步过程Fig.3 Synchronization process

首先,在分布式阶段运用TPSN建立各个节点的一跳邻居节点的动态时延表,每个节点会得到一跳邻居节点的时延,具体时延表如表1所示。这个阶段把网络中的节点进行编号,当时延表中包含所有的节点编号时,意味着时延表建立完成。此时,根据每个节点的时延表中所包含的节点个数进行参考节点的选取,把邻居节点较多的节点设置为参考节点,避免了始终使用同一个参考节点,使得参考节点的选取引入了一定的随机性。

表1 节点动态时延关系

当时延表建立完成并且参考节点确定后进入集中式同步,在参考节点上利用FTSP广播其本地时间,其他所有节点根据此时间以及本地的时延表更新它们的本地时间,并且把更新完成的时间广播出去。如果节点已经更新完成就丢弃收到的广播报文,否则进行更新,直到所有节点更新完成从而时间达到同步。具体同步过程如下。

步骤1各个节点发送同步请求包,接收来自一跳邻居节点的同步应答包,并建立与一跳邻居节点的时延表。在发送包的过程中,对每个发送包以及接受包的每个字节标记时间戳,为LWLR建立时间戳对。在这个过程中,若接受到的节点ID已经存在于时延表中则丢弃该请求包或应答包。

步骤2检查所有时延表中的节点ID是否达到系统中节点总数。若是,则计数各个节点时延表所包含的节点数,把包含节点数最多的那个节点设置为参考节点,并对各两节点之间进行LWLR拟合,得到拟合参数,进入第二阶段同步;否则各个节点继续发送同步请求包。

步骤3把参考节点设置为进行FTSP源节点,广播自己的本地时间,收到该时间包的节点根据时延表查找到对应的时延,并且根据相应拟合曲线计算该节点的时间,从而得到与发送节点的拟合时延,该拟合时延与时延表中的时延进行对比,从而进行本地时间调整,并设置状态为已调整,然后再把各自的本地时间广播出去,以让其邻居节点进行时间调整。若收到时间包的节点已调整好时间,则广播自己的本地时间。

步骤4检查所有节点的状态是否都为已调整,是则结束本次同步,否则参考节点继续广播当前本地时间。

3 仿真验证

对LWLR中的参数τ进行选择,测试环境为Python2.7,根据仿真表明,如图4所示,当τ=1.0时权重值很大,相当于所有样本点都是一样的权重,拟合出的曲线与线性回归是一样的。如图5所示,当τ=0.01时得到非常好的效果,体现了样本点间的特性。如图6所示,当τ=0.001时引入了太多的噪声点,出现了过拟合现象。所以,τ取0.01较为合适。

图4 τ=1.0时的拟合曲线Fig.4 Fitting curve when τ=1.0

图5 τ=0.01时的拟合曲线Fig.5 Fitting curve when τ=0.01

图6 τ=0.001时的拟合曲线Fig.6 Fitting curve when τ=0.001

把得到的参数τ值运用于LWLR中,对本文中的同步算法进行仿真实验,所使用的系统环境为Ubuntu-16.04,工具为ns-allinone-2.35[24]。仿真参数如表2所示,分别在不同节点数以及不同速度下对同步精度和分组数量进行仿真。TF-LIN表示TPSN和线性回归的FTSP,也就是基本的FTSP时间同步算法；TF-LWLR表示TPSN和LWLR的FTSP,即本文提出的对FTSP算法的改进。

表2 仿真参数

图7为不同算法完成同步过程发送同步分组数量的对比,可以看出,网络中节点数目越多,节点的一跳邻居节点也较多,完成同步所需的同步分组也增加。但TF-LIN和TF-LWLR要比单纯的TPSN增长缓慢且分组数量也比较少。由于TF-LIN和TF-LWLR只是对回归方式进行了优化,并不影响两者同步的分组数量,所以增长趋势大致相同。从图7中可以看出,本文提出的算法TF-LWLR相比经典TPSN在同步分组的传输数量方面平均降低了30%左右。

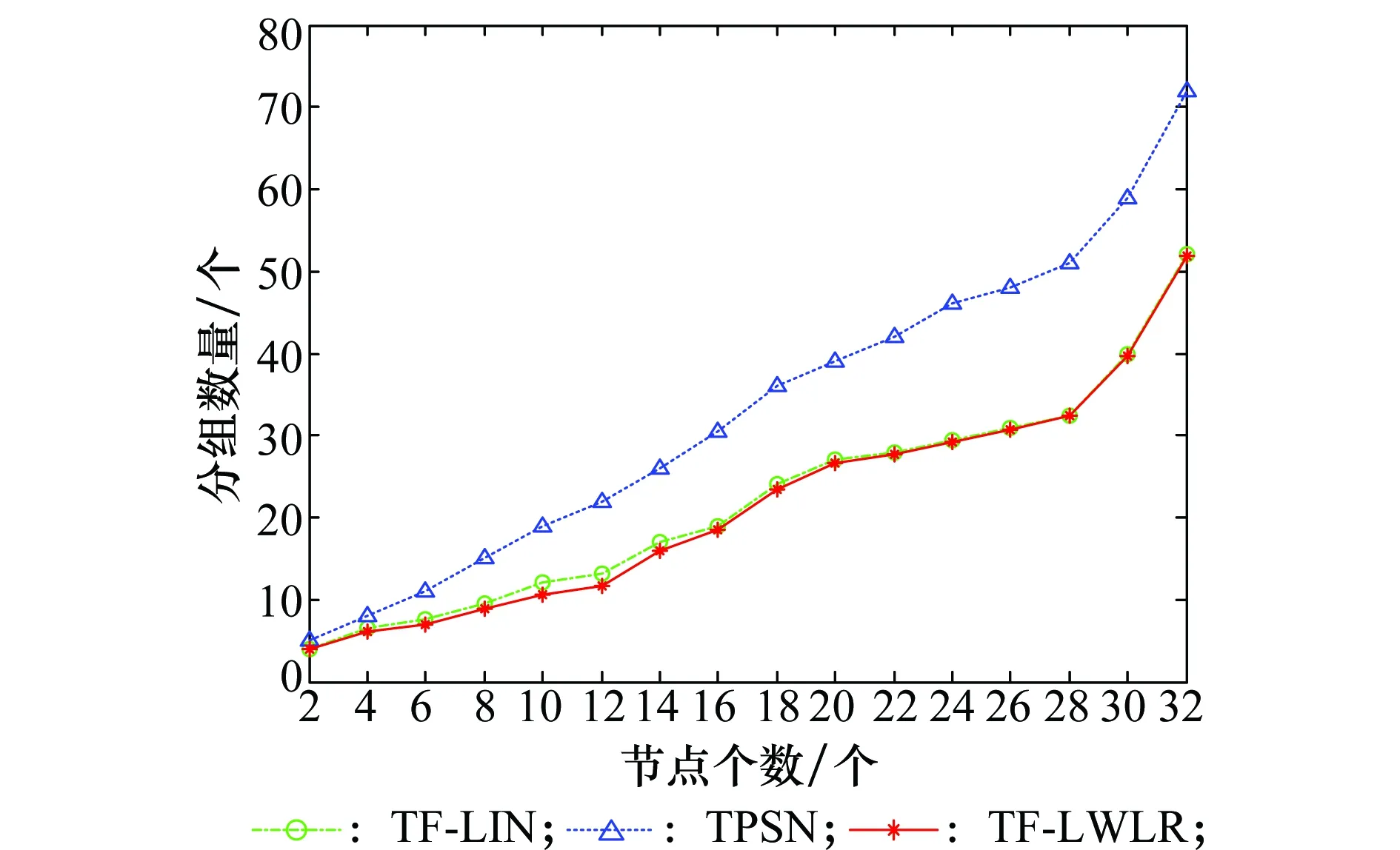
图7 不同节点数目的同步分组数量对比Fig.7 Comparison of synchronized packets number fordifferent number of nodes

图8为不同算法在不同速度下发送同步分组数量的对比,可以看出TF-LWLR随着网络中节点移动速度的增加,所需的同步分组传输数量要少于TPSN,但也表现出缓慢的递增趋势,因为当节点速度增加后,通信链路可能容易失效,使得部分数据包丢失,从而出现比较多的冗余分组。而TF-LIN和TF-LWLR递增趋势几乎重合,说明TF-LWLR在同步分组数量上与基本的FTSP效果相似,但优于TPSN。

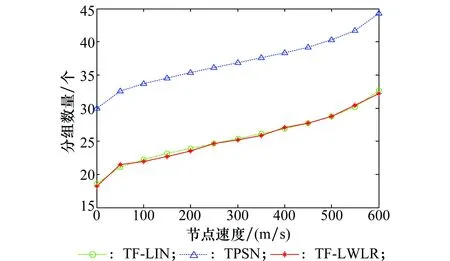
图8 不同速度的同步分组数量对比Fig.8 Comparison synchronized packets number at different speeds

为了对比各种算法在时间同步的精度方面的性能,本文用最大误差来体现,即同步完成后系统中选取某两个节点的最大时间误差的绝对值。由图9可看出,利用LWLR的TF-LWLR算法的同步精度要比其他两种算法要低,说明其能更好地对同步时间进行拟合。另外,网络规模越大,同步误差表现出越来越大的递增趋势,但TF-LWLR的增长趋势没有其他两种快速,说明其同步误差性能表现的要好。本文的算法使节点的同步精度提高了26%左右,而随着节点数目的增加,同步误差相对比较稳定、增长较慢。其次,随着网络节点数的增加,TF-LIN的同步误差要优于TPSN,说明TF-LIN更适用于大规模网络。

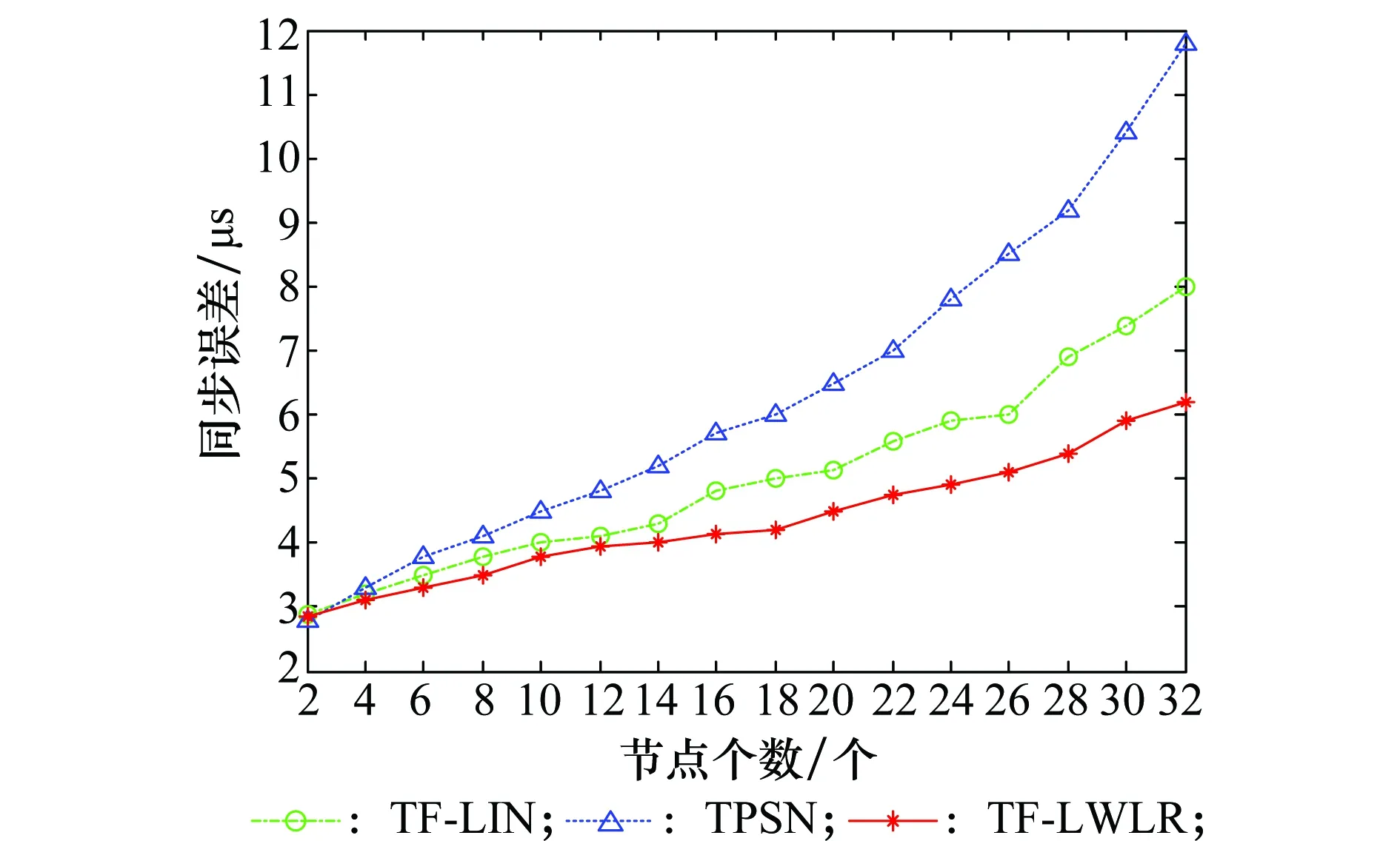
图9 不同节点数目的同步误差对比Fig.9 Comparison of synchronization errors for differentnumber of nodes

图10为不同算法在不同速度下同步完成后最大误差的对比,可以看出，TF-LWLR随着网络中节点移动速度的增加,最大误差也会呈现缓慢的递增趋势,同步精度受节点移动速度的影响较大。这是由于节点移动速度增加后,由于数据包丢失的严重性,从而使得同步时间延长,导致时钟漂移加重,进而导致同步精度的下降。但TF-LWLR随着节点速度的增加,同步误差要优于TPSN和TF-LIN,其更适用于动态拓扑网络。

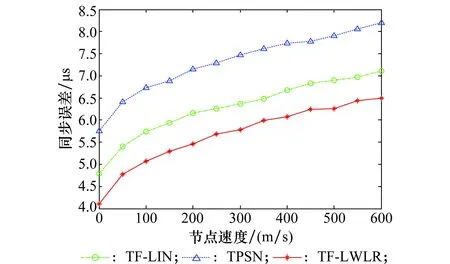
图10 不同速度的同步误差对比Fig.10 Comparison of synchronization errors at different speeds

4 结 论

本文对动态网络的特性提出一种时间同步算法,具体分为TPSN的时延建立以及FTSP的时间LWLR,这种方式既保证了合适的同步精度,又减少了同步过程所需的分组传输数量,一定程度上降低了同步延时。通过理论分析和仿真实验表明,该算法在动态网络中取得了良好的效果,对网络中节点数目变化具有鲁棒性。