基于功率制约的信息系统柔性构型方法研究∗

潘长鹏 汲万峰 韩玉龙

（海军航空大学 烟台 264001）

1 引言

随着信息时代的不断发展，人们需求的各种无线通信业务日益增加，支持各种无线业务的通信系统层出不穷、日新月异，无线频谱成为越来越紧缺的资源。虽然已存在的各种通信系统都在使用新技术提高其自身的频谱利用率，但有限的频谱资源也越来越不能满足日益增长的用户需求。从时域和空域的角度观察发现，静态授权分配的频段存在许多未被充分利用的“频谱空洞”，也就是频谱的利用率非常低，这与频谱资源日益短缺的问题互相矛盾［1］。因此认知无线电技术（CR）应运而生。

CR技术可以实现认知用户，也即次级用户在空闲频段上进行通信，空闲频段主要包括非授权频段和授权频段。在授权频段上进行通信就要求次级用户要具有认知能力，可以对其周围无线环境的历史和当前状况进行检测、分析、学习、推理和规划，以使用授权用户的空闲频谱信道资源进行通信，从而提高频谱的使用效率例。CR技术的出现，为解决频谱资源短缺，实现频谱动态管理以及提高频谱利用率开创了崭新的局面。

2 模型的建立

假定次用户有完美的频谱感知能力，次用户采用正交式频谱接入进行通信，次用户对频谱空洞的使用不会对主用户造成任何干扰。次用户感知到可用频谱后，要解决的主要问题就是各用户如何高效地使用空闲频谱。这时，可用的带宽也随之确定，次用户可以控制的资源就只有调制方式和发射功率。我们将不考虑用户所采用的具体信号调制方式，理想地认为用户采用了最适合信道传输的某种调制方式。在这样的条件下，次用户可控制的资源就只有发射功率了［2］。因此，该信息系统可以看作是功率维约束下的柔性系统构建问题，也是一个动态频谱管理问题。该问题可以描述为在已经准确感知到可用空闲频谱后，各次用户在频谱上合理分配功率，以实现频谱的高效使用。

假设有K个次用户，感知到N个空闲频段可以使用，在频谱管理算法执行过程中可用空闲频谱不发生变化，i表示次用户，n表示频段。第i个次用户在第n个频段功率分配情况表示，表示用户i的最大发射功率。显然，用户i分配的总功率不能超过其最大发射功率，即：

用户i的收益不仅与自己功率分配情况有关，还要受到其他用户的影响，因此用户i的效用（收益）函数可写为

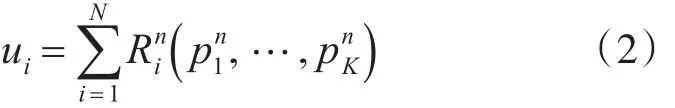
对于一个网络而言，衡量其性能的指标是各个用户效用的函数，因此该模型可写为如下形式的优化问题：

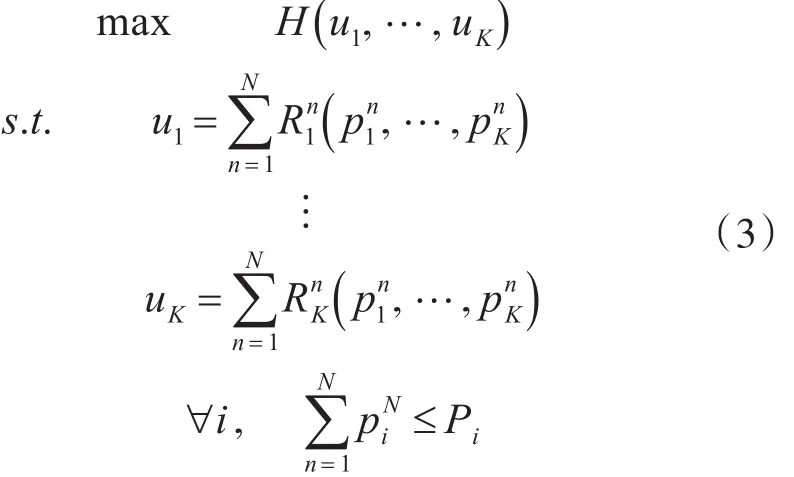
用户的效用函数可以根据实际应用背景的要求而变化，并不唯一。但是对于一个通信用户而言，他最关心的其服务质量，而其服务质量的一个重要的指标就是数据传输速率［3］。用户的传输速率不仅与自身的功率有关，还与其他用户的干扰有关，从信息论角度看，这是个干扰信道问题。众所周知，干扰信道的容量域目前还不知道，因此不能准确地写出用户速率的表达式。可做如下合理简化：假定用户发射的是复高斯信号，接收端的噪声为高斯噪声，不使用干扰消除技术，接收端仅把干扰作为高斯噪声处理。这样，用户i的效用函数可用下式表达：

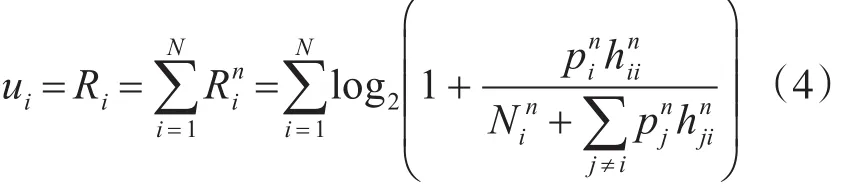
对于系统效用函数，有下面四种选择。

实际选用哪个作为系统性能指标则根据需要而定。

在上面建立了频谱管理的优化模型。但是，在上面任意的系统目标函数下，该问题几乎都是个NP-hard的问题，在当前理论下多项式时间内找到其最优解是不可能的。下面我们采用博弈论方法来求解此问题［4］。

之所以采用博弈论的方法，是出于以下几方面的原因。第一，动态频谱管理问题是一个次用户之间争夺频谱资源的问题，一个次用户的行为会对其他次用户的收益造成影响。而博弈论正是研究冲突的数学，所以该问题与博弈论研究的内容性质比较吻合，可以放到博弈论的框架下分析。第二，博弈论提供了多种不同的最优性准则，即均衡点。不同的应用场景下，可以采用不同的均衡定义或者博弈类型对问题进行分析，而不是仅限于最优化问题，博弈所带来的这种方便性是优化所不具备的。第三，应用非合作博弈理论可以有效地寻找解决动态频谱管理问题的非中心式方法，特别是在无法建立中心控制机制的时候，这种非中心式的方法就更加重要。而且从目前来看，无线通信越来越向着分布式的方向发展，在这个背景下，探讨动态频谱管理的非中心式方法也有其重大意义［5］。

3 动态频谱管理的非合作博弈求解

3.1 数学模型

优化问题是从系统的角度来看问题，因此目标函数是对整个系统总体性能的一个描述。博弈与优化的一个区别在于，博弈是从每个局中人的角度来看待问题。对于非合作博弈而言，局中人关心的只是自己的利益，而不关心对其他局中人的影响［6］。每个局中人追求的是自身利益的最大化。因此，对于动态频谱管理问题，其非合作博弈模型可以用策略式描述如下：

1）局中人：次用户，i=1，2，…，K

与优化模型相比，博弈模型中并没有考虑系统的效用函数，这在一定程度上简化了计算复杂度，同时也不能保证系统效用函数有很好的性能。此外，非合作博弈中，用户间不协作，没有或者有非常少的信息交流，这就为动态频谱管理的非中心式实现提供了可能性［7］。

3.2 均衡点存在性

对非合作博弈问题最重要的是找到其纳什均衡点，因此均衡点的存在性是个很重要的问题。动态频谱管理博弈是个策略空间连续的博弈问题，其效用函数是连续的，纳什的存在性定理并不能直接适用于该问题，但这类博弈的混合策略纳什均衡点仍然一定存在。而在混合策略均衡点，发送端的功率并不确定，而是以一定的概率采用一定功率发送，这无疑会增加系统的复杂性，实现起来并不简单。因此，我们更关心的是纯策略纳什均衡点。

定理：令G表示策略式非合作博弈。如果对任意局中人i，其策略空间Si是个非空紧凸集，效用函数ui()

s是s的连续函数，是si的拟凹函数，则博弈G至少有一个纯策略纳什均衡点。

考虑动态频谱管理博弈，局中人i的策略空间：

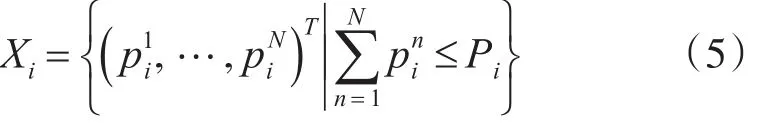
该空间是个紧凸集。局中人i的效用函数：

容易验证效用是s的连续函数和si的凹函数，因此也是si的拟凹函数。所以该博弈问题至少存在一个纯策略纳什均衡点［8］。

3.3 均衡点求解

上面已经证明了系统博弈均衡点的存在性，现在的问题就是如何找到均衡点。一般来讲求解纳什均衡是个复杂度很高的问题，但根据前面介绍的博弈最优响应动态可以部分地解决频谱管理博弈均衡点求解问题。该思想最早由Yu Wei等提出并用于处理DSL中的功率控制问题，也是目前为止应用最广泛的方法之一［9］。

对于次用户i而言，当其他次用户的策略固定后，最优响应就是如下优化问题的解：

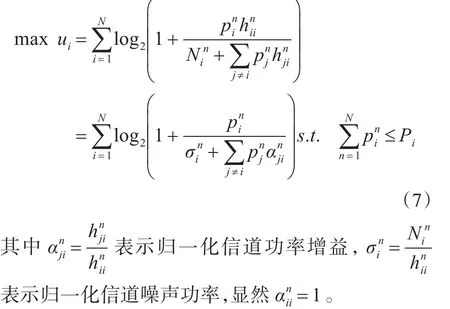
因为假定其余次用户策略不变，所以次用户i的效用函数的分母是个常数，该优化问题就是一个凹问题，与信息论中经典的并行信道最优功率分配问题类似，采用拉格朗日乘法可以得到解为［10］

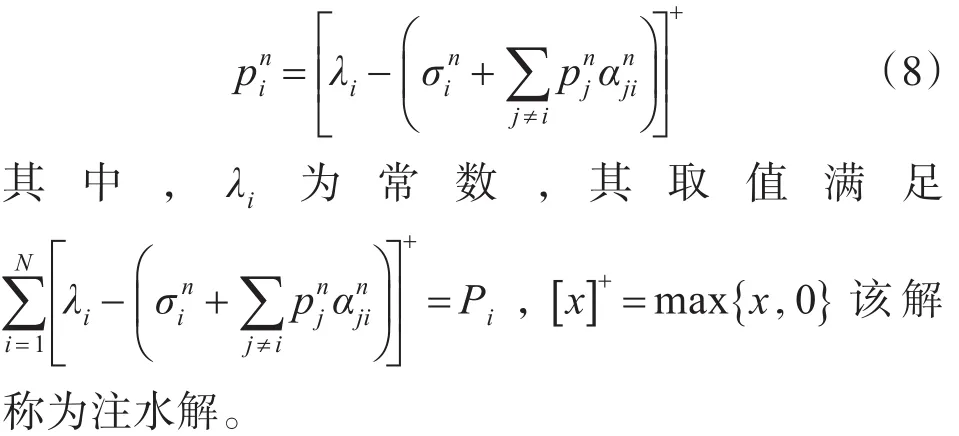
有了最优响应函数，下面的问题就是如何让次用户同时满足最优响应条件。该过程可以采取两种迭代方案实现，一种是Gauss-Seidel迭代方法，另一种是Jacobi迭代方法［11］。

1）Gauss-Seidel方法：每个博弈阶段，仅有一个次用户依据最优响应函数更新策略，其余次用户保持不变［12］：

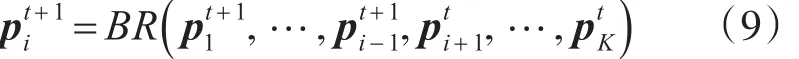
2）Jacobi方法：每个博弈阶段，所有次用户认为其他次用户的策略不变，同时按最优响应函数更新策略［13］：

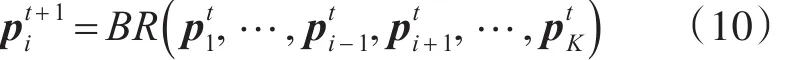
根据这两种不同的方法，可以得到两个求解纳什均衡点的迭代算法［14］。

（1）采用Gauss-Seidel迭代方法

对所有次用户，初始化功率分配向量 pi=0，初始化迭代次数t=0。

重复迭代

（2）采用Jacobi迭代方法

对所有次用户，初始化功率分配向量 pi=0，初始化迭代次数t=0。

重复迭代

两种算法可统称为迭代注水算法。两种算法的区别主要在于次用户更新策略的顺序不同，算法1中用户i要等前i-1个用户完成更新后才计算更新自己的最优策略，算法2中所有次用户都在同一时刻计算最优策略并更新。因此当网络中次用户数较多时，算法2的速度要更快，但这种迭代方式也更容易进入循环状态，从而不能收敛。对于两种算法，都要求次用户相信，在自己更新功率时，其余次用户保持先前策略不变，该要求在实际中是合理的。如果有多个均衡点，两种方法收敛到的均衡点不一定相同。初始点不一定要选用零点，这里选用零点仅是为了简单［15～16］。

4 结语

本文在基于功率制约的信息系统柔性构型方法研究过程中，给出了求解纳什均衡点的迭代注水方法，纳什均衡的基础是完全信息非合作博弈。完全信息，具体到迭代注水算法中就是次用户发送端要可以准确得到目标通信对间的信道功率增益及各个信道受到的干扰。然而在实际信息系统中，完全准确地估计信道功率增益是不可能的，估计值或多或少都会有误差存在，此时完全信息非合作博弈已经不再适用描述这种情况。信道估计值存在误差，可理解为次用户的信息不完全。传统博弈论中，处理不完全信息的工具是由Hars提出的贝叶斯博弈，该博弈使用概率论的方法建模系统中参数的不确定性，因此该方法要求有不确定性参数的概率分布信息，这往往使得处理的问题变得非常复杂，而且概率分布信息能否得到也是个问题。对此在下一步研究中可以使用稳健博弈的方法处理信息不完全性。