基于粒子群算法的多无人机任务分配
李士波

摘要:多无人作战飞机任务分配是无人机协同控制的一项关键技术。综合无人机后续攻击任务和影响无人机作战效能评估的各种因素,按照分阶段分配方法建立了多UCAV任务分配模型,并使用粒子群算法对建立的任务分配模型进行求解,将每个粒子的位置使用两个多维向量表示,两个向量分别采用两种不同方式同时进化。该方法解决了分配模型复杂性带来的分配难题,取得了良好的分配效果。
关键词:任务分配;协同控制;无人作战飞机;粒子群优化
DOI:10.11907/rjdk.173133
中图分类号:TP319
文献标识码:A文章编号:1672-7800(2018)007-0193-03
Abstract:Multi-UCAVmissionallocationisthekeytechniqueforcoordinatecontrol.Consideringtheconsequentattackmissionandthemainfactorsthataffectcombatefficiencyassessment,themissionallocationmodelthatbasedondifferentstagesisestablished.Particleswarmoptimizationalgorithmisproposedtosolvetheproblem,eachparticlespositionisexpressedintwomulti-dimensionvectorsandthevectorsevolveindifferentmannerssynchronously,theevolvevalueisusedincostevaluationsubsequently.Thismethodhassolvedtheallocationproblemthatbroughtaboutthecomplexityoftheallocationmodelandreceivedgoodallocationresults.
KeyWords:missionallocation;coordinatecontrol;unmannedcombataerialvehicle;particleswarmoptimization(PSO)
0引言
無人作战飞机(UnmannedCombatAerialVehicles,UCAV)从事的任务具有很大的危险性和复杂性,因此通常采用多架无人机共同执行任务的策略[1-3]。在多架无人机共同执行任务过程中,多UCAV任务规划技术是实现多无人机协同控制的关键技术[4-6]。因此,多UCAV任务分配技术研究尤其重要。
多无人机任务分配问题是一个多目标组合优化问题,即通过一定的分配策略给无人机分配不同的任务。分配原则是在保护无人机的前提下,增大对目标的杀伤概率,避免重复攻击和遗漏。
多UCAV任务分配问题是研究热点[7-9],学者们先后提出了匈牙利算法、线性规划法、禁忌搜索方法、市场交易模型等方法,这些方法在分配规模较大时会导致求解困难,并且往往未能充分考虑影响无人机作战效能的各种因素和后续攻击任务,很难适应动态复杂环境下无人机任务分配需求。
本文提出按阶段分配的方法建立多UCAV任务分配模型,在建模过程中充分考虑影响无人机作战效能评估的各种因素,并提出使用粒子群算法对建立的复杂任务分配模型进行求解。该分配方法对无人机数目和攻击目标数目均没有限制,无人机可先后对多个目标进行攻击,在分配过程中并不简单地要求每一架无人机都执行攻击任务,更好地反映了任务分配的实际情况和要求。
1多UCAV任务分配模型建立
在多UCAV任务分配问题中,每架无人机可赋予攻击多个目标,因此可将多无人机任务分配过程划分为多个阶段,如图1所示。在每个阶段中,选择一架无人机去攻击一个目标,在每个分配阶段不仅要考虑选择无人机攻击目标,还要考虑选择执行攻击任务的无人机。
无人机任务分配要考虑的因素包括执行攻击任务的次序、无人机对目标杀伤的概率、无人机对抗威胁的能力(生存概率)、攻击路径最短等。执行攻击任务的次序指在攻击目标确定后,为每架无人机首先确定攻击哪一个目标,之后确定要攻击的第二目标,依次类推,直至所有攻击目标均被确定。任务分配目标是使无人机对目标的杀伤概率达到最大而自身的损失最低,并尽可能地使所有无人机攻击路径总和最短[10-11]。
式(3)表示在每个阶段中只有一架无人机从事攻击任务,并只对一个目标发起攻击。式(4)表示无人机攻击的目标数目最多不能超过其自身能力的限制。
2粒子群算法
粒子群算法是Kennedy和Eberhart[12-13]于1995年提出的一种优化算法,该算法被证明在优化问题方面具有很大潜力。与传统算法相比,PSO算法有一定的智能性,具有适用范围广、搜索能力强、不易陷入局部最优等优点,在路径规划领域效果非常好[14]。
粒子群算法本质是一种基于群体和适应度的优化算法[15-16]。在求解优化问题时,每个粒子代表问题的一个潜在解。粒子群算法使用适应度函数评估粒子优劣,适应度函数的大小由粒子的具体位置坐标决定。每个粒子记忆、追随当前的最优粒子,在解空间中搜索。每次迭代过程不完全随机,如果找到较优解,将会以此为依据寻找下一个解。
每个粒子用3个指标表征:位置、速度、适应度。在进化前,粒子的初始位置和速度根据问题限制在一定区间内任意取值。粒子在每次迭代过程中需要记忆更新两个极值。第一个极值是粒子自身历史上的最优位置,另一个极值是整个种群目前的最优解。所有粒子通过这两个极值修正粒子自身的位置,对下一步行为进行调节,使之迅速向最优值方向收敛。每个粒子在多维空间中不断改变位置,直到一个相对稳定的位置被找到,或者到达设定的进化次数限制。所有粒子按照下式演化:
Rand1()函数和Rand2()函数在[0,1]之间产生随机数。C1和C2是一个正常数,作为权重因子。权值ω用于控制粒子以前的速度对现在粒子速度的影响,在一定程度上,该参数平衡全局和局部粒子搜索能力。
用Vpbest表示粒子过去经历的所有位置中的最好位置时产生的速度矢量,用Vgbest表示在所有粒子中经历的最好位置所产生的速度矢量,绘制粒子自身位置变化原理如图2所示。
3任务分配问题粒子群算法
针对复杂任务分配模型的粒子群方法需要构造一个2Nt维空间,每个粒子都包含两个Nt维向量,分别定义为Target和Vehicle向量。Target向量对应于在不同阶段所要攻击的目标,Vehicle向量则对应于不同阶段攻击时所使用的无人机。例如使用3架无人机去打击5个目标,则某个粒子的位置向量如表1所示。
攻击过程划分為5个阶段:①序号为3的无人机攻击目标2;②序号为1的无人机攻击目标4;③序号为2的无人机攻击目标3;④序号为3的无人机攻击目标1;⑤序号为1的无人机攻击目标5。要保证所有目标均分配给一架无人机攻击,无人机可使用多次但不能超过其最大攻击次数。
在粒子群进化中,Target向量和Vehicle向量采用两种不同的方式同时进化。由于Target向量代表不同阶段要攻击的目标,每个目标只能攻击一次,因此Target向量定义为有序整数数列:
其进化可通过离散PSO算法进行。Vehicle向量对应于不同阶段攻击时使用的无人机,将其定义为序列Y=(u1,u2…uNv),ui∈U。
Vehicle向量与Target向量的区别在于Vehicle向量允许重复,并且有最大攻击目标数的限制。因此,Vehicle向量的进化采用标准PSO算法变形,实现方法及过程如下:
(1)每个粒子的位置中Vehicle向量的每一维随机取1-Nv(目标数)之间的整数,其中1-Nv代表无人机序号。
(2)为了保证满足约束条件(4),考察生成的序列,若Vehicle向量中某个无人机的序号出现次数超过无人机最大攻击的目标数目,则重新生成该向量,直到满足约束条件为止。
(3)与Vehicle向量相对应的速度向量V2为-(Nv-1)~(Nv-1)之间任意值。
(4)结合Target向量,按照代价评估函数(2)计算个体历史最优解和群体全局最优解。
(5)按照速度更新公式和位置更新公式计算Y和V2,对Y取整,当Y和V2超过边界限制时按边界取值。若更新后某个粒子的位置Y不满足约束条件(4),则恢复更新前的原值。
(6)重复执行步骤(4)和步骤(5),直到满足终止条件或达到最大迭代次数。
4任务分配问题仿真实现
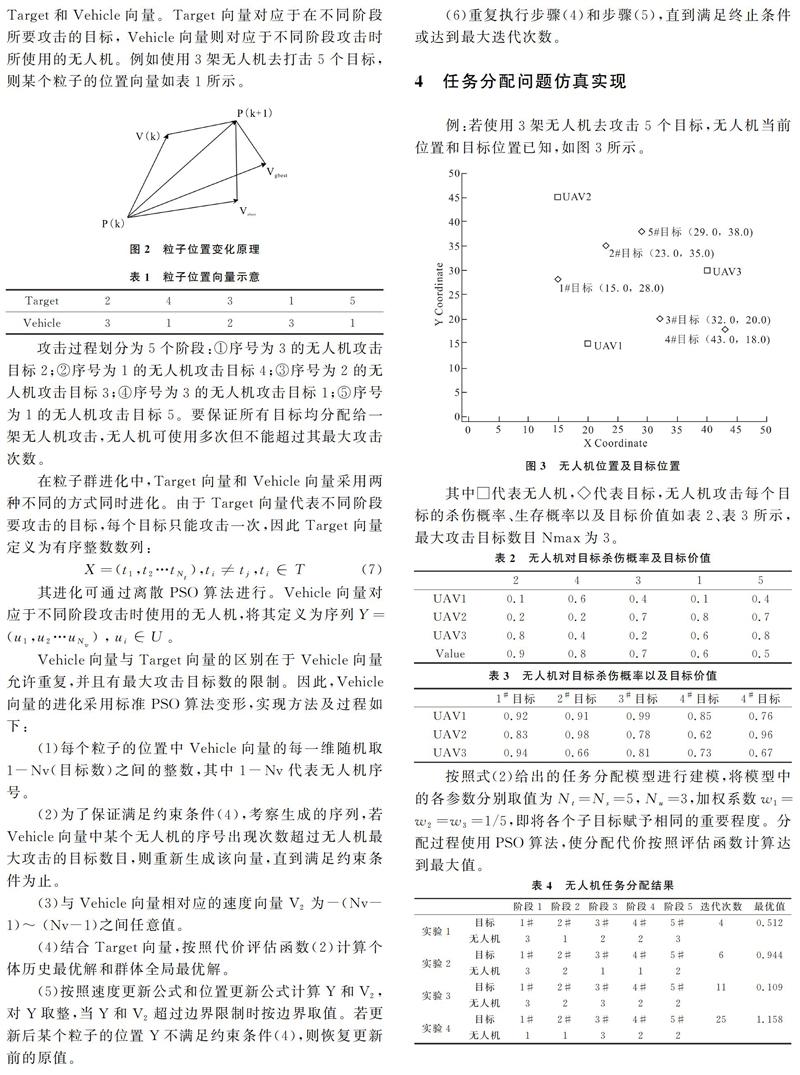
例:若使用3架无人机去攻击5个目标,无人机当前位置和目标位置已知,如图3所示。
其中□代表无人机,◇代表目标,无人机攻击每个目标的杀伤概率、生存概率以及目标价值如表2、表3所示,最大攻击目标数目Nmax为3。
按照式(2)给出的任务分配模型进行建模,将模型中的各参数分别取值为Nt=Ns=5,Nu=3,加权系数w1=w2=w3=1/5,即将各个子目标赋予相同的重要程度。分配过程使用PSO算法,使分配代价按照评估函数计算达到最大值。
5结语
本文采用分阶段分配方法建立无人机任务分配模型,该模型充分考虑了无人机对目标的杀伤概率、目标对抗威胁能力和攻击路径长度等重要战术指标,并考虑了无人机对后续目标的攻击任务。建立的复杂任务分配模型使用粒子群算法求解,将每个粒子的位置使用两个多维向量表示,两个向量采用两种不同方式同时进化。仿真结果证明了该方法的可行性,本文提出的建模方法和分配算法可直接应用到多无人机自主控制体系中。
参考文献:
[1]刘重,高晓光,符小卫,等.未知环境下异构多无人机协同搜索打击中的联盟组建[J].兵工学报,2015(12):2284-2297.
[2]龙涛,沈林成,朱华勇.面向协同任务的多UCAV分布式任务分配与协调技术[J].自动化学报,2007(7):731-737.
[3]曹文静,徐胜红.多无人机协同方法研究[J].飞航导弹,2007(1):44-48.
[4]肖作林,田鸿堂,秦枫.多UCAV协同任务规划技术研究[J].战术导弹技术,2013(6):53-57.
[5]张红,卢广山,朱荣刚.无人作战飞机任务系统技术研究[J].电光与控制,2006(1):55-59.
[6]邸斌,周锐,丁全心.多无人机分布式协同异构任务分配[J].控制与决策,2013(2):274-278.
[7]闵桂龙,端木京顺,张冰,等.军事后勤中的多目标无人机任务规划[J].计算机仿真,2016(3):85-89.
[8]TAKENOT,TSUJIMURAY,YAMAZAKIG.Asingle-phasemethodbasedonevolutioncalculationforvehicleroutingproblem[C].ConferenceofComputationalIntelligenceandMultimediaApplications,2001:103-107.
[9]UCHIMURAK,SAKAGUCHIH,NAKASHIMAT.Geneticalgorithmsforvehicleroutingproblemindeliverysystem[C].Yokohama:VehicleNavigationandInformationSystemsConference,1994.
[10]TANK,LEEL,ZHUQ,etal.Heuristicmethodsforvehicleroutingproblemwithtimewindows[J].ArtificialIntelligenceinEngineering,2001,15(3):281-295.
[11]叶媛媛,闵春平,朱华勇,等基于整数规划的多任务分配问题研究[J].信息与控制,2005,34(5):548-552.
[12]EBERHARTRC,KENNEDYJ.ANewOptimizerusingparticleswarmtheory[C].Proceedingofthe6thInternationalSymposiumMicroMachineandHumanScience,1995:39-43.
[13]KENNEDYJ,EBERHARTRC.Particleswarmoptimization[C].ProceedingsofIEEEInternationalConferenceonNeutralNetwork,1995:1942-1948.
[14]张建南,刘以安,王刚.基于优化粒子群算法的无人机航路规划[J].传感器与微系统,2017(3):1-4.
[15]吴晓军,杨战中,赵明.均匀搜索粒子群算法[J].电子学报,2011(6):1261-1266.
[16]王东风,孟丽,赵文杰.基于自适应搜索中心的骨干粒子群算法[J].计算机学报,2016(12):2652-2667.
(责任编辑:杜能钢)

