板球系统的PSO优化模糊RBF神经网络PID参数研究
王长正 向凤红 毛剑琳


摘要:板球系统是一个典型的多变量、非线性控制系统。针对板球系统在PID控制中震荡大、精度低、实时性差等问题,应用拉格朗日方程对板球系统在忽略干扰因素条件下进行数学建模,采用粒子群算法对模糊RBF神经网络初始参数进行优化,并设计RBF神经网络与模糊PID控制相结合的控制方法。在MATALB环境下完成板球系统定位实验,仿真结果表明,经粒子群优化模糊RBF神经网络的PID参数后,提高了板球系统的定位精度,并增强了系统控制的实时性。
关键词:板球系统;粒子群算法;模糊RBF神经网络;MATLAB;PID
DOI:10.11907/rjdk.173124
中图分类号:TP301
文献标识码:A文章编号:1672-7800(2018)007-0014-05
Abstract:Ballandplatesystemisamultivariable,nonlinearandcomplexunderactuateddynamicsystem.Accordingtothefixed-pointcontrolofballandplatesystem,weestablishthemathematicalmodeloftheLagrangeequationignoringtheinterferencefactorsofballandplatesystem.Aimingattheproblemsinballandplatefixed-pointcontrolsystem,suchasconcussion,lowprecisionandpoorreal-time,wedesignthecontrolmethodbycombiningRBFneuralnetworkwithfuzzyPIDcontrol,andtheinitialparametersoffuzzyRBFneuralnetworkareoptimizedbyparticleswarmoptimization.ThepositioningcontrolsimulationexperimentofballandplatesystemiscompletedinMATLABenvironment,thesimulationresultsshowthatPIDparametersoffuzzyRBFneuralnetworkwhichoptimizedbyparticleswarmoptimizationcanimprovetheprecisionoftheballandplatesystemfixed-pointcontrolandthereal-timenessofthesystem.
KeyWords:ballandplatesystem;particleswarmoptimization;fuzzyRBFneuralnetwork;MATLAB;PID
0引言
板球系统是一个典型的非线性系统,具有强耦合、欠驱动和无约束的特点,是球杆系统的二维扩展,可用于验证控制算法的有效性。板球系统也是欠驱动系统的典型代表,对其控制算法的研究可以提高实际系统的可靠性。因此,自20世纪80年代以来,很多学者开始将板球系统作为控制领域验证各种控制算法的benchmark对象[1-5]。文献[6]采用直接自适应模糊控制与滑模控制相结合的方式,引入蚁群算法对系统参数进行優化,减弱了板球系统轨迹跟踪控制中的震荡,提高了板球系统的轨迹跟踪精度;文献[7]设计一种间接模糊自适应控制器,将监督、间接模糊自适应与自适应补偿3种控制算法相结合,保证了板球系统的稳定性并减小误差至零邻域内;文献[8]设计基于粒子群算法优化PID参数的控制器,对PID参数进行在线调节,并通过在球杆系统上的验证,显示了智能优化算法在PID参数调节中的优越性,但对于强耦合、非线性板球系统,智能优化算法仍存在局部搜索能力弱与非线性逼近能力差的缺点。因此,设计一种高效控制器,对提高板球的控制跟踪精度具有重要意义。
为提高板球系统的控制精度,本文将善于表达模糊和定性知识,具有人类思维推理方式的模糊逻辑与具有自组织、自适应能力的RBF(RadialBasisFunction)神经网络相结合,并采用粒子群算法对模糊RBF神经网络进行优化,设计了模糊RBF神经网络PID控制器,从而改善了模糊控制器依赖度强、缺乏自学自能力的缺点。最后使用PID控制器与本文提出的算法完成对板球系统的定位控制实验,通过实验结果对比验证本文算法的有效性。
1板球系统建模
本实验采用固高GBP2001型板球系统作为实验平台,板球系统物理模型如图1所示,板球系统各项参数如表1所示。板球系统因其自身的复杂性,建模过程中作以下4点假设对模型进行简化与线性化:①小球在平板上没有滑动和绕小球垂直中心轴旋转的运动;②不考虑板的角度和面积限制;③小球和平板始终接触;④忽略小球和平板间的所有摩擦。
基于以上假设建立模型,利用牛顿定律或拉格朗日方程[9],通过动力学分析,可得到如式(1)、式(2)所示的完整非线性耦合的板球系统动力学方程。
式(1)、式(2)建立的非线性模型在线性控制的实际操作中难以应用,因此将其线性化,得到:
2粒子群算法
2.1粒子群算法描述
2.2基于PSO优化模糊RBF神经网络的方法
采用PSO算法对模糊RBF神经网络进行训练,在粒子编码中写入模糊隶属度函数的中心值、宽度和连接权值,并进行连续迭代找到最优值作为网络参数,然后通过网络学习得到目标网络。
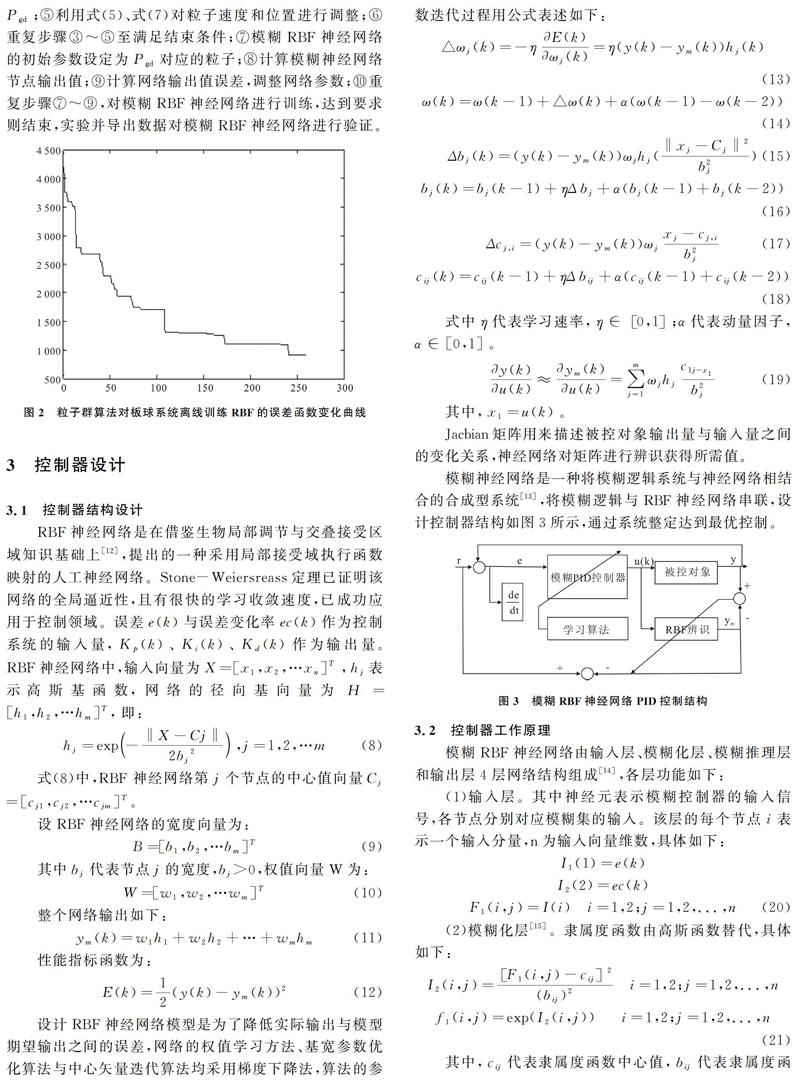
基于粒子群优化的模糊RBF神经网络学习算法按以下步骤进行[11]:①粒子群总数为100,迭代次数为260次,权重因子c1=c2=2,粒子搜索定义域(-Xmax,Xmax),初始化粒子速度和位置;②按式(9)计算粒子适应度,Pid为粒子初始化位置,Pgd为适应度最小的粒子;③对比每个粒子当前适应度与初始化位置Pid,若更优,则更新Pid;④对比每个粒子Pid与Pgd的适应度,若更优,则更新Pgd;⑤利用式(5)、式(7)对粒子速度和位置进行调整;⑥重复步骤③~⑤至满足结束条件;⑦模糊RBF神经网络的初始参数设定为Pgd对应的粒子;⑧计算模糊神经网络节点输出值;⑨计算网络输出值误差,调整网络参数;⑩重复步骤⑦~⑨,对模糊RBF神经网络进行训练,达到要求则结束,实验并导出数据对模糊RBF神经网络进行验证。
3控制器设计
3.1控制器结构设计
设计RBF神经网络模型是为了降低实际输出与模型期望输出之间的误差,网络的权值学习方法、基宽参数优化算法与中心矢量迭代算法均采用梯度下降法,算法的参数迭代过程用公式表述如下:
Jacbian矩阵用来描述被控对象输出量与输入量之间的变化关系,神经网络对矩阵进行辨识获得所需值。
模糊神经网络是一种将模糊逻辑系统与神经网络相结合的合成型系统[13],将模糊逻辑与RBF神经网络串联,设计控制器结构如图3所示,通过系统整定达到最优控制。
3.2控制器工作原理
模糊RBF神经网络由输入层、模糊化层、模糊推理层和输出层4层网络结构组成[14],各层功能如下:
(3)模糊推理层。模糊化层与模糊推理层相互连接,达到模糊规则准确匹配的目的,节点之间进行模糊运算。
4板球系统仿真实验
为了验证本文提出的控制方法,本次实验采用固高GBP2001型板球系统作为实验平台,按照图2所示的结构搭建控制系统。初始PID参数为Kp=0,Ki=0和Kd=0,RBF神经网的隐含层节点数目为6。在上述参数设定条件下,利用本文设计的模糊RBF-PID控制器对固高GBP2001型板球系统进行仿真实验,其中控制参数Kp、Ki和Kd在控制过程中输入输出间的RBF-PID参数变化曲线如图5所示,板球系统的小球位置跟踪变化曲线如图6所示。
设计PID控制器并以定位小球于板的中心为控制目标,图7显示了PID控制器控制系统的输出效果。小球在板上的误差变化趋势如图7(a)所示,小球运动轨迹如图7(b)所示。可以看出小球在板上的位移偏差较大,在实际系统控制中已经触碰球板边缘,系统运行10s后,小球在板上达到稳定状态。
设计模糊RBF-PID控制器,在板球系统的实际操作中导出小球运行结果数据并进行分析。图8显示了模糊RBF-PID控制器的控制系统输出效果,小球的位置跟踪误差变化如图8(a)所示,小球在板上运动轨迹如图8(b)所示。由图可以看出,小球在板上的位移偏差减小了很多,运动轨迹较为简洁,达到稳定状态的时间缩短至6s。
PID控制与模糊RBF-PID的控制结果对比如表2所示。从表中可以看出,模糊RBF-PID控制器相较于PID控制器效果更好,精确度和时效性都有一定程度提高。
5结语
由于板球系统具有多变量、开环不稳定和非线性等特性,被广泛应用于控制算法研究中,其中定位控制研究对非线性系统控制的理论研究具有重要意义。本文采用基于粒子群算法优化的模糊RBF-PID控制方法对板球系统进行定位控制,仿真验证了粒子群算法的引入可提高板球系统定位控制的稳定性和精度,并增强了板球系统控制的实时性。下一步工作是建立更精确的板球系统数学模型,包括球板间摩擦与传动机构、步进电机等环节,完成板球系统的轨迹跟踪,从而实现小球在板上的避障运动。
参考文献:
[1]HANKW,TIANYT,KONGYS,etal.TrackingcontrolofballandplatesystemusingaimprovedPSOon-linetrainingPIDneuralnetwork[C].2012IntConfonMechatronicsandAutomation.NewYork:CurranAssociates,2012:2297-2302.
[2]王紅睿,田彦涛.板球系统的参数自调整反步控制[J].控制与决策,2009,24(5):749-753.
[3]王红睿,田彦涛.一类欠驱动系统的非线性输出跟踪控制[J].控制与决策,2011,26(6):953-956.
[4]段慧达,田彦涛,李津松,等.一类高阶非线性系统的级联自抗扰控制[J].控制与决策,2012,27(6):216-220.
[5]TIANYT,BAIM,SUJT.Anon—linearswitchingcontrollerforballandplatesystem[J].InternationalJournalofModelling,IdentificationandControl,2006(3):177-182.
[6]翟晨汐,李洪兴.板球系统的直接自适应模糊滑模控制[J].计算机仿真,2016,33(2):383-388.
[7]韩京元.非线性板球系统的监督分层智能自适应控制算法研究[D].长春:吉林大学,2014.
[8]RANAMA,USMANZ,SHAREEFZ.Automaticcontrolofballandbeamsystemusingparticleswarmoptimization[C].InternationalSymposiumonComputationalIntelligenceandInformatics,2011:529-534.
[9]赵艳花,邵鸿翔.基于视觉的板球控制系统研究[J].自动化技术与应用,2011,30(10):12-15.
[10]徐云云.基于视觉的板球控制系统算法研究[D].成都:西华大学,2012.
[11]段明秀.基于PSO优化的模糊RBF神经网络学习算法及其应用[J].当代教育理论与实践,2012,2(1):101-104.
[12]李炜,张美玲.基于模糊RBF神经网络的管道泄漏检测方法[J].兰州理工大学学报,2009,35(6):79-83.
[13]胥良,郭林,梁亚,等.基于模糊RBF神经网络的智能PID控制[J].工业仪表与自动化装置,2015(6):67-75.
[14]於东军,王士同.模糊神经网络模型及其建模应用研究[J].华东船舶工业学院学报,1998,12(2):22-28.
[15]张巍.基于差分演化算法的电梯群智能控制系统研究[D].沈阳:东北大学,2008.
(责任编辑:黄健)

