一种浮地磁控忆阻模拟器设计与特性分析
(常州大学信息科学与工程学院,江苏常州213164)
二十世纪七十年代,根据电路变量组合完备性的原理,蔡少棠教授预测了直接关联电荷和磁通两个变量的电路元件— “忆阻器”的存在性[1],并建立了忆阻器件与系统理论[2]。近十年前,惠普实验室Strukov等[3]在 《自然》上首次报道了忆阻器的物理实现,从而迅速激发了忆阻器及其应用电路的研究热潮。但是因为忆阻采用的纳米技术,在具体实现和制作上存在着巨大的困难,目前还未作为一个实际的元件走向市场。因此设计一种忆阻等效电路并用其替代实际忆阻器进行实验和应用研究具有重要意义。
文献[1]中最早提出了忆阻模拟器概念及其设计方法,其后出现了多种采用已有的模拟分立元器件实现忆阻的等效电路,如基于HP TiO2忆阻[3+4]、二次和三次非线性磁控忆阻[5-7]等数学模型的等效实现电路,以及利用模数混合电路和超大规模数字电路实现的电路[8]。上述等效电路都是以输出端“接地”方式工作的,不能任意接入电路,在应用时会受到一定的限制。因而,文献 [9-12]提出了“浮地”方式的等效电路。文献 [9]中基于通用电路元器件提出了一种浮地忆阻等效模拟电路,使用运算放大器和乘法器以及电阻、电容实现,但是该等效电路输出端电流io实际上是由外围电路决定的,而不是输入端流进的电流i,意味着自身不能确保两端的输入和输出电流相等,该忆阻等效电路不支持用于模拟规范式忆阻元件。文献 [10]基于文献 [9]的电路,采用两个电流传输器AD844作为电流镜,解决了电流不相等的问题。文献 [11]基于电流传输器,与乘法器AD633、接地电容以及部分电阻设计了一种新的浮地电路模拟器,并进行了硬件电路实现。文献 [12]采用四个AD844组合成了第二代电流传输器,实现了另一种新的浮地忆阻模拟器。因此采用电流传输器作为电流镜是实现浮地忆阻模拟器较为可靠的方案。
本文基于忆阻的定义提出了一种新的磁控忆阻模型,采用通用模拟集成电路芯片完成了该忆阻浮地电路模拟器的设计。该忆阻模型由线性电阻和随时间变化的非线性电阻两部分构成,本文定义一个非线性电阻参数对其频率特性进行分析,阐述忆阻伏安特性中 “8”字型紧磁滞回线变化的机理,并通过Multisim仿真软件和硬件电路测试研究验证其基本的电特性。
1 磁控忆阻的浮地电路模拟器设计
对于一个忆阻元件的定义是:如果一个二端元件,在任一时刻的磁通量φ(t)和电荷量q(t)之间存在代数关系

这一关系可以由φ-q或q-φ平面上的一条曲线所确定,则此二端元件称为忆阻元件。当式(1)由电荷的单值函数表示时,即φ(t)=φ(q(t)),称其为电荷控制型忆阻;相应地,当式(1)由磁通的单值函数表示时,即q(t)=q(φ(t)),称其为磁通控制型忆阻。因此,磁通控制型忆阻(简称磁控忆阻)流过电流i(t)和两端电压v(t)之间的伏安关系可表示为
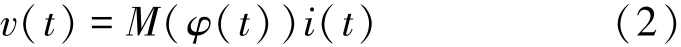
其中,M(φ(t))=1/W(φ(t));
W(φ(t))=dq(φ(t))/dφ(t)。
式中:W(φ(t))是磁控忆阻的忆导;M(φ(t))则为忆阻。由此,本文新提出的一种磁控忆阻模型可描述为
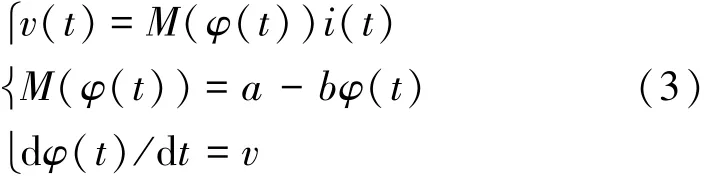
式中:a、b是正常数。
由式(3)可知,对于忆阻M(φ(t)),有
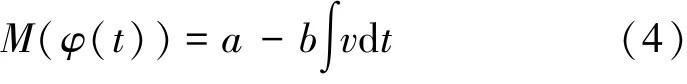
所以电路模拟器设计包括三部分工作:一是电压积分电路的设计,实现磁通φ的功能;二是控制电路设计,实现式(4)的功能;三是电流产生电路以及电流镜像电路的设计,实现浮地功能。其中,主要涉及到电流积分以及乘法运算等,上述运算关系可采用通用运算放大器、乘法器等模拟集成芯片实现。为使所设计的忆阻模拟器可以方便地任意接入电路使用,需要考虑其二端口的浮地设计。具体实现电路如图1所示,这里,模拟器端口电压为u(t)=v1-v2,端口电流为iin。
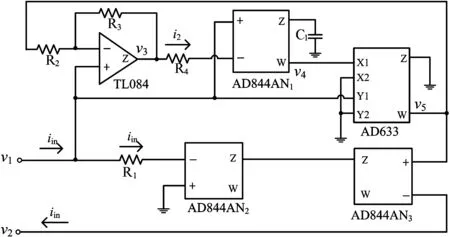
图1 有源浮地磁控忆阻电路模拟器Fig.1 A flux-controlled floating memristor emulator
图1中,AD844AN为电流传输器,具有以下特点:v+=v-,vw=vz,i+=0,i-=iz。 AD844AN2与AD844AN3构成电流镜像电路,由于AD844AN的负端电流跟随 Z脚电流,所以输入电流iin从AD844AN2负端传输到AD844AN3负端进行输出,实现浮地的功能,其中,输入、输出电流iin=v1/R1,电压v2=v5。
运算放大器TL084与电阻R2、R3实现减法运算,v3电压为

当R3=R2时, 有v3=2v2-v1。
AD844AN1与R4电阻以及电容C1构成了积分运算电路,v4为电容C1上的积分电压,则
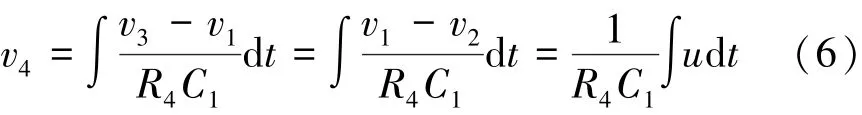
对于磁通φ有φ(t)=∫udt,所以,式(6)可写为

对于四输入乘法器AD633芯片,主要完成积分电压v4与输入端电压v1之间的乘法运算,W端口为输出电压v5,根据乘法器AD633的工作原理,输出电压v5=v2=v1v4/10。所以由上述分析可得图1所示忆阻电路模拟器的二端口电压为

将v1=R1iin代入式(8),可得

将式(9)与式(4)比较可知,当a=R1,b=R1/(10R4C1),图1所示电路实现了本文所提出的磁控忆阻模型。本文所设计的磁控忆阻电路模拟器参数为:R1=R2=R3=R4=20 kΩ,C1=1 μF。
2 浮地忆阻模拟器的基本电特性分析
对于图1提出的磁控忆阻模拟器,假设输入电压u(t)=Asin(2πft),其中,A为幅值、f为频率,则
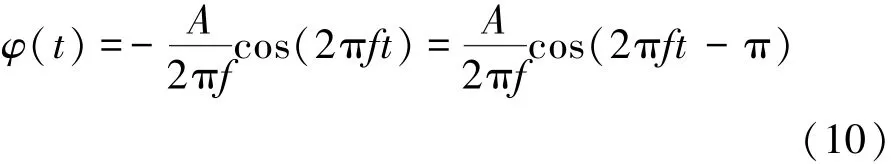
将上式代入式(4),可得
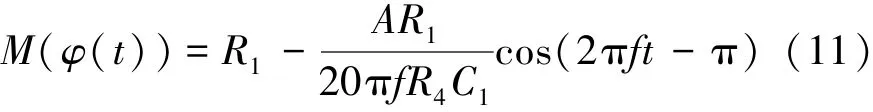
可见,该忆阻由线性电阻和随时间变化的非线性电阻两部分构成,而非线性电阻随着信号频率的增大逐步减小到零。定义一个非线性电阻参数k为

可以看到,参数k取决于输入信号的幅值A和频率f。当频率增加或者幅值减小时,k减小;反之,k增大。同时还应注意到,R4电阻和电容C1构成的时间常数也会影响k值,信号频率要与时间常数相适应。具体可分为以下三种类型:
1)当k趋近于0,即输入信号频率无穷大时,忆阻非线性特性消失,表现为线性电阻;
2)当k趋近于1,即时,忆阻的紧磁滞回线将达到最大;
3)当k远远大于1,即f≪20πR4C1/AR1,输入信号的周期大于模拟器电路的时间常数时,忆阻的磁滞回线消失。
在图1所示电路参数设置下,在忆阻模拟器端口施加不同的交变激励电压,采用Multisim软件研究本文所设计的忆阻模拟器的基本电特性。在图1的端口施加正弦电压u(t)=Asin(2πft),选取A=4 V和f=100 Hz,测试输入电压u(t)和输入电流i(t),可得结果如图2所示,其中,(a)为正弦电压激励下忆阻模拟器的电压和电流时域波形,(b)为正弦电压激励下磁控忆阻模拟器在电流-电压平面上的I-V回线。从图中可看出端电压和电流具有相同的零点,但流经忆阻的电流峰值超前于忆阻两端的电压峰值,即表现出 “记忆”特性,同时其伏安关系曲线具有 “8”字型紧磁滞回线特性。
进一步地,基于Multisim仿真平台,在图1所示电路的端口施加正弦激励电压u(t)=Asin(2πft),分别改变电压的幅值A和频率f,观察忆阻的电流与电压之间的曲线。为了比较不同频率及不同幅值变化时忆阻的电流-电压关系曲线的变化情况,画出不同正弦电压信号激励下,本文所设计的磁控忆阻模拟器的电流-电压关系曲线如图3所示,其中,(a)为固定幅值4 V,取不同的频率;(b)为固定频率20 Hz,取不同的幅值。由图3可见,当在图1所示电路端口施加正弦交变电压时,其电流与电压同时过零点,电流-电压关系曲线呈现紧磁滞回线。当固定激励信号的幅值时,随着频率的逐渐增大,I-V回线逐渐向内收缩,直至退化为一条直线。结果说明,当激励信号频率很高时,忆阻将退化为线性电阻,而失去其记忆性;当固定激励信号的频率时,随着电压幅值的逐渐减小,I-V回线逐渐向内收缩,直至退化为线性函数。仿真结果显示忆阻模拟器输入端口的关系曲线不仅与输入电压的频率有关,而且与输入电压的幅值有关,这与上文中非线性电阻参数k分析的结论是一致的。

图2 正弦电压激励下忆阻模拟器的伏安特性Fig.2 Current-voltage characteristics of memristor emulator with sinusoidal voltage stimulus
3 硬件电路实现及性能测试
图1所示的硬件电路实现的实物图照片如图4所示。其中,U2、U3、U4选取电流传输器AD844N芯片,U1选取运算放大器TL084芯片,U5选取乘法器AD633JN芯片,并在积分电容上并联一个电阻Rm,以避免积分器U2的DC电压积分漂移。

图3 不同正弦电压激励下的紧磁滞回线Fig.3 Pinched hysteresis loops under different sinusoidal voltage stimuli

图4 磁控忆阻器的硬件电路Fig.4 Hardware circuit of the flux-controlled memristor
在v1、v2端加入正弦激励电压,分别改变电压的频率和幅值,测量本文所设计的忆阻模拟器的端口特性,其测量结果如图5所示。其中,横坐标代表端口电压,纵坐标代表端口电流;图(a)中固定输入正弦信号激励幅值为4 V,频率分别取20,40,1 kHz,测得不同频率下磁控忆阻模拟器的伏安特性曲线;图(b)为固定输入正弦信号激励频率为20 Hz,幅值分别取4,3,2 V,测得不同幅值下磁控忆阻模拟器的伏安特性曲线。

图5 不同正弦电压激励下的I-V回线Fig.5 Pinched I-V loops under different sinusoidal voltage stimuli
可以看出,低频时设计的磁控忆阻模拟器的伏安特性曲线在第一、三象限中呈斜 “8”字形状,随着频率的逐渐增大,斜 “8”字I-V回线逐渐变窄,最终退化为一条直线;当激励信号幅值减小时,I-V回线单调缩小,最终变成一个线性函数,这与电路仿真结果相吻合。
4 结论
忆阻具有广泛的应用前景,然而实际的忆阻器仅存在于实验环境中,其商品化还需要一个漫长的过程,根据其电学特性构建其等效电路模型来进行研究具有重要意义。本文通过分析忆阻的定义,提出了一种新型磁控忆阻模型,并基于电流传输器AD844等通用电路元器件构建了可任意接入电路使用的浮地忆阻电路模拟器。该忆阻值由线性电阻和随时间变化的非线性电阻两部分构成,由非线性电阻参数分析了该忆阻模型的频率特性,结论表明非线性电阻受输入信号的幅值和频率以及电路中R4电阻和电容C1构成的时间常数的影响。基于Multisim软件,对不同交变电压信号以及不同参数设置下的电流-电压关系进行了仿真,完成了硬件电路的搭建与测试。实验结果表明:所设计的磁控忆阻模拟器具有斜体“8”字紧磁滞回线特性,与理论上的忆阻模型特性相吻合。同时,通过修改本文电路的控制电路模块,如增加乘法器等,还可实现二次、三次等磁控忆阻电路模拟器。本文研究结果进一步充实了忆阻理论成果以及实验手段,为忆阻在电子学领域的应用提供了一种器件模拟实体。

