基于IPD 工艺的小型化无反射带通滤波器设计
刘 赣,邢孟江,李小珍,李 楠,杨晓东
(1.昆明理工大学信息工程与自动化学院,云南昆明 650500;2.昆明学院信息技术学院,云南昆明 650500)
随着通信技术的不断发展,对于无源器件的性能要求不断提高,高性能、低成本、小型化成为无源器件设计的重点。滤波器作为无源器件中的一个重要组件,是射频电路中不可或缺的一部分[1]。传统滤波器设计电路,是通过阻带把不希望通过的信号反射回信号源,这将对系统的通信性能造成巨大的影响。在传统滤波器的研究基础上,如何实现滤波器阻带信号无反射正逐渐成为一个学术研究热点[2-11]。
无反射滤波器也称为吸收式滤波器,它区别于传统滤波器最大的特点是它将阻带信号吸收掉而不是反射回信号源,可以极大地提高电路的线性度。在国外,无反射滤波器的研究已经展开[2-6]。2010年,Morgan和Boyd首次提出了无反射滤波器概念,给出了低通、高通、带通、带阻四款无反射滤波器的电路拓扑及设计方法,并且基于印制电路板(PCB)工艺,采用分立元件,设计并加工了4阶325 MHz无反射低通滤波器和中心频率210 MHz、带宽200 MHz的无反射带通滤波器,级联方式为传统滤波器设计方法中的串联级联[2-4]。2016年,韩国的Lee等[5]开始研究一阶无反射带通滤波器,采用集总式表面贴装器件(SMD),设计并加工了一款中心频率为95 MHz,BW-3dB≤30 MHz的无反射带通滤波器。2017年,伊朗科技大学的Amirhosseini和Taskhiri在研究Morgan提出的无反射滤波器基础上,设计了一种任意奇数阶和任意阻带衰减的无反射低通滤波器的电路原型,并加工了一款三阶中心频率为40 MHz,阻带衰减As=20 dB的无反射低通滤波器[6]。
随着国内集成电路的发展,无反射滤波器的理论和设计研究变得非常有意义。同时,很多人开始寻求新的工艺技术来进一步实现滤波器结构的小型化,IPD工艺凭借其体积小、价格低和兼容性高等优点,逐渐成为研究的热点[7-10]。如表1所示,给出了几种基材设计滤波器的参数对比。
目前,在国内,有关无反射带通滤波器的论文还比较少,还处在起步阶段,2014年,电子科技大学的秦巍巍等[11]仿真设计了一款通带中心频率为3500 MHz,BW-3dB≤479 MHz,IL≤3 dB,VSWR<2的新型吸收式微带线带通滤波器。2017年,电子科技大学的张钰英、胡诗锦等仿真设计了一款中心频率为70 MHz、IL≤4dB、BW-3dB≤4.5 MHz及BWab(吸收带宽)∶BW-3dB≥10的正交相位的吸收式带通滤波组件,有效地吸收了带外返回信号[12]。本文首次提出在高电阻硅衬底上利用IPD工艺设计了一种中心频率为2.3 GHz,中心频率的插入损耗小于1 dB,插入损耗3 dB处带宽为1.91 GHz,带外抑制峰值大于14.47 dB的小型化无反射带通滤波器,整体尺寸仅为1.6 mm×1.25 mm×0.3 mm。本文提出的基于IPD工艺的无反射带通滤波器具有高性能、小尺寸、与半导体工艺兼容性高以及超宽带等特点,并且可加工成贴片形式,便于与其他微波组件集成,适合批量生产。
1 基本理论
1.1 偶模和奇模分析
关于无反射滤波器本文做出的简化假设之一是结构须是对称的,以便能在输入输出端口实现良好的阻抗匹配。从对称网络(图1(a))开始,想象将电路沿着其对称平面分开,裸露出占据电路中心节点的导线,如图1(b)所示。可以为这个双端口定义两种不同类型的激励,即偶模和奇模[13]。
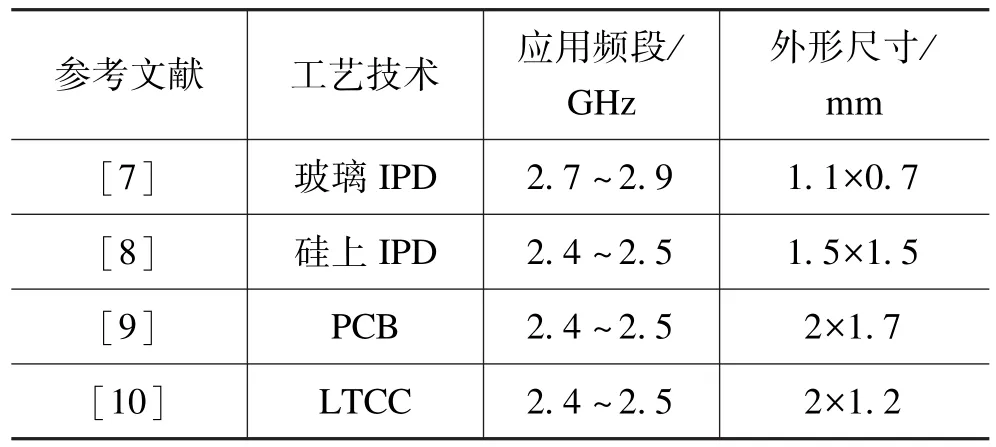
表1 几种基材设计滤波器参数对比Tab.1 Comparison of filter parameters for several substrate designs
偶模激励的特点是将两个相同的信号同时输入到两个端口中,那么任何一个对称点都有相同的相位。偶模激励下,很明显,没有电流可以流过对称面的导线(电流通过对称面的方向是不确定的)。所以,如图1(c)所示,只画了一半的网络,并用开路代替对称面,这半个电路被称为偶模等效电路。当用偶模激励进行刺激时,这个等效电路单端口的反射系数被称为Гeven。
奇模激励的特点是将相同的信号同时输入到两个端口中,但有180°相位差,因此端口2的信号是端口1信号的负值。在这种情况下,接触对称平面的任何节点上都不会产生相对于地的电压(电压的极性不能确定)。所以,如图1(d)所示,再画一次网络的一半,并用虚拟的短接地代替对称面,这半个电路被称为奇模等效电路。当用奇模激励进行刺激时,这个等效电路单端口的反射系数被称为Гodd。

图1 对称的双端口网络Fig.1 Symmetric dual-port network
因此,双端口网络的反射系数将是偶模等效电路的反射系数Гeven和奇模式等效电路的反射系数Гodd的叠加,不难得到

因此,为了使电路无反射,即
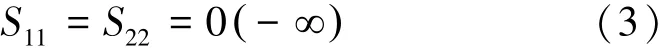
必须确保偶模和奇模的反射系数幅度相等而符号相反,实现完美输入匹配条件。
联立式(1)(2)(3)不难得出

由式(4)(5)可推导得出,原始双端口网络的传递函数直接由偶模反射系数决定,归一化的偶模输入阻抗等于归一化的奇模输入导纳,反之亦然。
1.2 对称性和对偶性
对称性和对偶性的概念,是本文无反射滤波器拓扑结构的基本原理。一个拓扑网络的奇模和偶模等效半电路是同时对称并且对偶的。对偶性的概念要追溯到麦克斯韦方程组中电场和磁场的对称性,在这种情况下,电路的对偶由电容器交换电感器和并联元件交换串联元件等构成[13]。
关于无反射滤波器,为了能在输入端和输出端实现良好的阻抗匹配,不妨设计成对称结构。对称的结构使拓扑规范化,为对偶性的拓扑电路推导提供了便利,为以后模型的设计简化埋下了伏笔。对称性对偶性确保了偶模和奇模电路具有大小相等、方向相反的反射系数。这样,偶模和奇模的等效半电路足以完整地描述对称双端口网络的性质。
2 无反射带通滤波器的设计
2.1 无反射低通滤波器的设计
有了前面的一些理论知识的铺垫,低通滤波器设计过程就顺理成章了。首先将偶模等效电路画成高通滤波器[14],将奇模等效电路画成偶模式的对偶,如图2(a)所示。接下来,做如下拓扑变换:
图2(b),偶模一侧:交换最后的电容和串联的终端电阻的位置;奇模一侧:改变第一个电感和终端电阻的接地连接,由绝对接地变为虚拟接地。
图2(c),偶模一侧:在输入节点和对称平面之间添加一个电感。相似地,在电阻和对称平面之间添加一个开路连接线(因为对称平面是一个开路电路,所以这些元件对电路没有影响);奇模一侧:在对称平面(虚短)到地之间添加一个电容(因为电容的两端被短路了,所以电容对电路也没有影响)。
图2(d),最终无反射低通滤波器的拓扑结构。
对称性和对偶性限制了电路元件可能具有的值。例如,图2(d)中奇模式等效电路中的第一个电感L2必须是偶模式等效电路中第一个电容C1的对偶,则有如下等式[15]

然而,通过对称,偶模的第一个电容C1又必须等于奇模旁边的对应电容C2。电容C2又是偶模下的下一个元件(电感器L3)的对偶,以此类推。无论原型阶梯网络的顺序如何,最终结果都是一个等式链
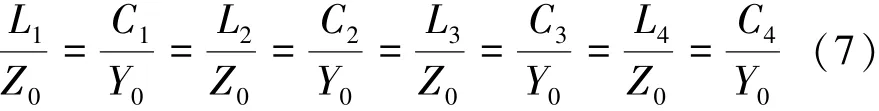
则得出所有电感L相等,所有电容C相等的结论。式中Z0为特征阻抗,Y0为特征导纳,两者互为倒数关系。图2(d)中,R1、R2必须相等,并且它们互为对偶,则R1=R2=Z0。
2.2 无反射高通滤波器的设计
既然无反射低通滤波器已经设计出来,那么将它变换成无反射高通滤波器就很简单了,利用频率变换可得无反射高通滤波器的电路图如下
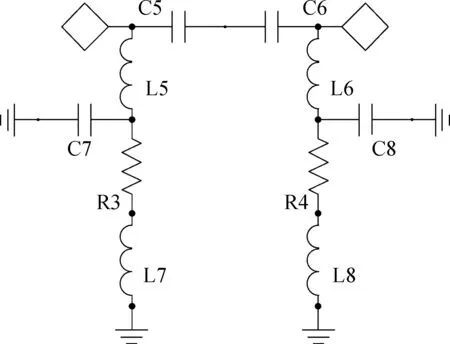
图3 无反射高通滤波器的拓扑Fig.3 Reflectionless high-pass filter topology
同理,在图(3)中有图(2)中相同的理论推导,不难得出电容C5=C6=C7=C8,电感L5=L6=L7=L8, 电阻R3=R4=Z0且L/C=Z20。
2.3 无反射带通滤波器的设计
为了得到想要的带通无反射滤波器的电路图,将无反射低通和高通滤波器进行串联(增加带宽)得到如图4所示的带通滤波器拓扑,图中C3=2C1(为了简化模型),其他结论没有变化。
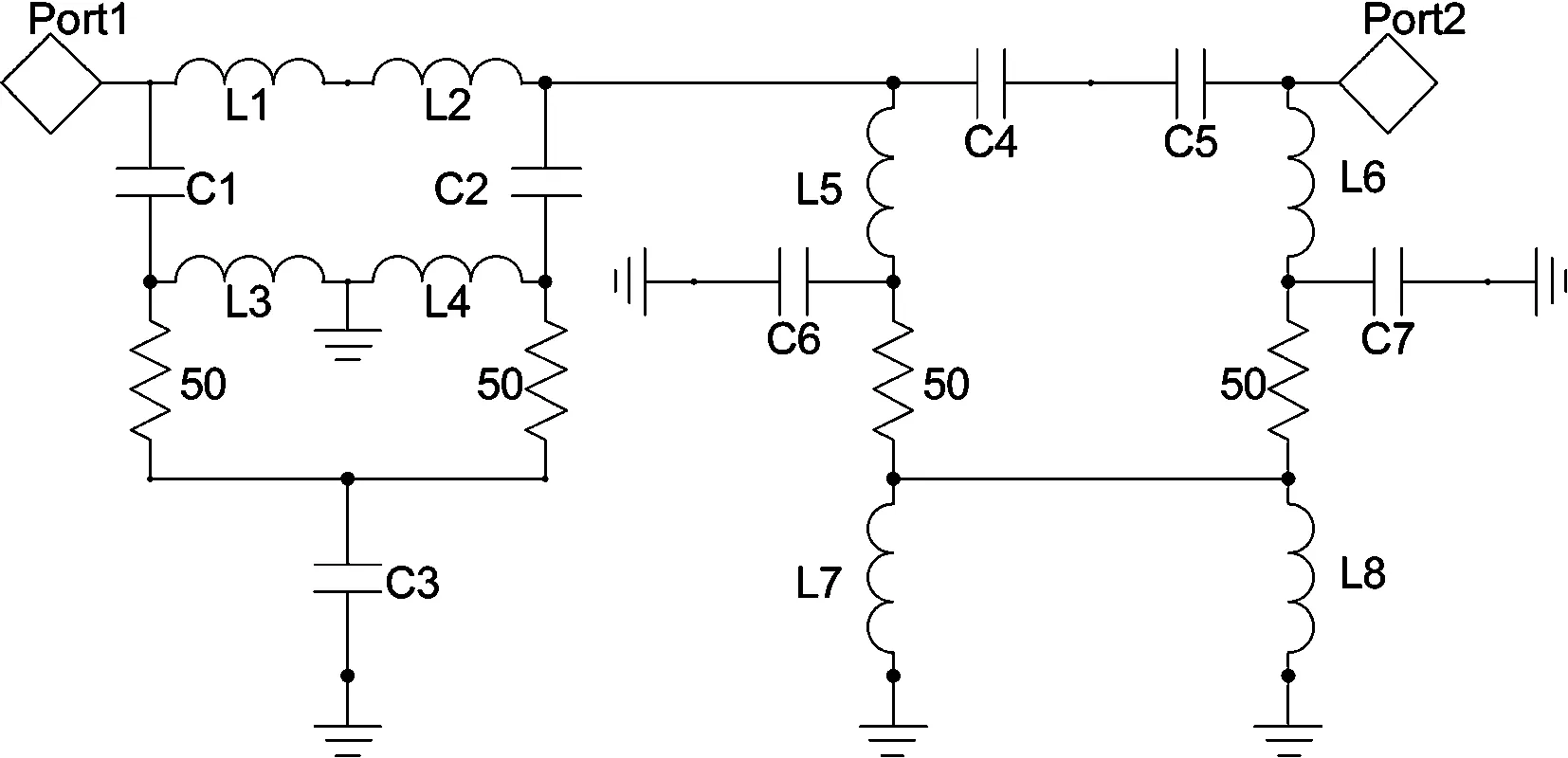
图4 无反射带通滤波器的拓扑Fig.4 Reflectionless band-pass filter topology
通过Ansoft designer电路仿真软件可以得到各元件值的初始值为L1=L2=L3=L4=1.840 nH,C1=C2=C3/2=0.744 pF,L5=L6=L7=L8=5.363 nH,C4=C5=C6=C7=2.145 pF,R1=R2=R3=R4=50 Ω。并仿真了无反射带通滤波器的电路图,得到仿真结果如图5所示,回波损耗S11在50 dB处浮动,插入损耗S21如图所示,电路仿真结果表明该电路结构具有良好无反射带通滤波器的性能。
3 滤波器的模型及仿真
IPD工艺采用的是薄膜工艺,笔者采用LC集总方式在HFSS建立滤波器模型,电感选择的是平面螺旋电感,利用硅平面刻蚀技术实现。电容选择的MIM(金属M1-绝缘介质-金属M2)电容,通过在平行板之间填充高介质材料可以提高电容量。电阻是由质量分数82%Ni(镍)和18%Cr(铬)组成,通过磁控溅射共沉积方法获得精准电阻。滤波器的整体尺寸为1.6 mm×1.25 mm×0.3 mm,三维模型结构如图6所示。
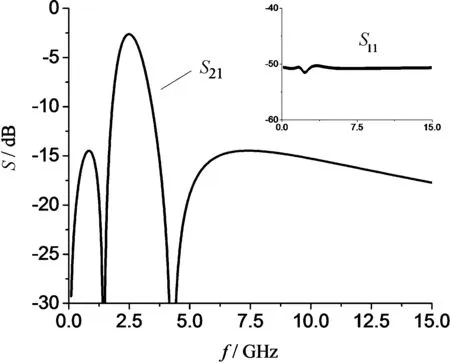
图5 电路模型仿真结果Fig.5 Simulation results of circuit model

图6 无反射带通滤波器的三维结构Fig.6 Three-dimensional structure of reflectionlessband-pass filter
在此三维结构中,电感L1~L8均采用螺旋电感方式,且低高通模型各自电感值相等,方便了模型的构建与调试。为了提高电容的精度,电容C1~C7层与层之间有5 μm的错层(M1层、介质层和M2层之间前后左右各隔5 μm)。为了减小寄生效应的影响,模型中S与C1、C1与C4、C5与S的连接线及C6、C7的接地线皆设置为40 μm线宽。模型的输入输出端放在两边,方便级联。模型均采用通孔接地的方式来实现接地。用HFSS对无反射带通滤波器的三维结构进行仿真,得到回波损耗(S11)和插入损耗(S21)波形如图7示,造成偏差的主要原因是由于电感电容产生的寄生效应,基本满足无反射带通滤波器的要求。由图7可以看出,无反射带通滤波器的中心频率为2.3 GHz,中心频率的插入损耗小于1 dB、插损3 dB处带宽为1.91 GHz、带外阻带抑制峰值大于14.47 dB。

图7 无反射带通滤波器仿真结果图Fig.7 Diagram of reflectionless band-pass filter simulation results
4 结论
本文首次基于IPD工艺设计了一款无反射带通滤波器。与大多数无反射带通滤波器设计所不同的是,本文是基于无反射高低通滤波器的拓扑结构,通过串联方式得到超宽带的无反射带通滤波器的拓扑结构,从而在HFSS中完成模型的构建与仿真。该滤波器中心频率为2.3 GHz,插损3 dB处带宽为1.91 GHz,带外峰值阻带抑制大于14.47 dB,回波损耗一直保持大于8.5 dB,整体尺寸仅为1.6 mm×1.25 mm×0.3 mm。结果表明此款无反射带通滤波器对反射信号具有良好的吸收性,将其应用在混频器或高增益放大器中,会大大提高系统性能。本文通过设计仿真验证了基于IPD工艺小型化无反射带通滤波器的可行性,为今后关于无反射滤波器的设计与研究提供了理论指导。

