电迁移不同失效模式的微观机理及其有限元寿命预测

张继成,张元祥,王 静,梁利华

(1.浙江工业大学机械工程学院,浙江杭州 310014;2.衢州学院机械工程学院,浙江衢州 324000)

互连焊点在微电子芯片封装结构中有着举足轻重的作用,其不仅提供了芯片和基板之间的电气连接,而且是芯片到基板的散热通道,并为芯片提供机械支持。随着微电子封装逐步向微型化、轻量化、高性能发展,互连焊点的电流密度急剧增加,如今焊点的尺寸已达到了微米级别[1],使得通过焊点的电流密度达到甚至超过1×108A/m2。在这种高电流密度的驱使下极易引起焊点的电迁移失效问题[2],并造成互连电路的破坏而导致巨大损失。

当前对电迁移的试验研究主要针对不同的微互连材料以及电迁移过程中出现的金属间化合物和孔洞的影响等[3-4]。其中,部分学者注意到了电迁移的两种失效模式:由IMC的大量生成及原子的显著迁移引起的失效;由微孔洞的聚合及裂纹的扩展引起的失效。针对这个问题,人们主要研究了其与电迁移过程中电阻的变化之间的关系。而根据Lin等[5]的研究,当出现由微孔洞的聚合及裂纹的扩展引起的失效时,电阻会在长时间的稳定之后迅速上升;而当出现原子的显著迁移时,电阻会在上升到一定程度后保持稳定。Chen等[6]对出现这两种现象的条件进行了统计分析,然而对其出现的原因并没有给出合理的解释。

本文通过对BGA封装结构施加不同电流密度及温度,研究了焊点的电迁移失效现象,并对上文所述两种电迁移失效模式进行了分析。结合SEM扫描电镜结果,从原子扩散剧烈程度的角度对其进行了解释。同时,对于电迁移理论在描述这种现象的能力上,本文通过原子密度积分算法对试样在不同载荷条件下的电迁移寿命进行了预测,并与试验结果进行对比,指出了目前电迁移理论的局限性以及改进方案。

1 电迁移加速试验

1.1 BGA电迁移试验试样

本文试验中所用的芯片为Fairchild半导体公司的产品,型号为FDMA8051L。该芯片的D1,D2,D5,D6四个引脚互连,图1为芯片示意图及原理图。而在本文试验中,仅考虑D2,D5这两个引脚下的焊点电迁移现象,即将电流分别施加在D2,D5两个焊点,并通过芯片内部电路形成完整回路。凸点互连结构的制备采用倒装焊(Flip Chip)工艺,并由上海凝睿电子科技有限公司完成PCB板的制作及整体试样的回流焊接。

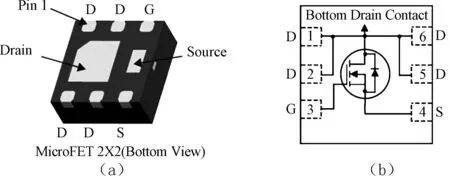
图1 FDMA8051L(a)芯片及逻辑原理图(b)Fig.1 FDMA8051L type chip and its logic schematic diagram

针对BGA焊点测试试样的制备,采用倒装焊接(Flip Chip)工艺,通过二次回流之后将芯片通过无铅焊料SAC305(Sn96.5Ag3.0Cu0.5)焊接到自行设计的PCB电路板上,得到试验所使用的BGA封装结构试样,如图2所示。

1.2 试验方法

试验过程中,将互连焊点封装试样连接至电源及电压测试端,并设置恒温箱环境温度为固定值。这里选取温度为120℃以及150℃作为环境温度,同时选取1.4×108A/m2以及1.9×108A/m2两种电流密度用于正交对比。芯片上下表面贴装热电偶(PT200),并利用导热硅胶保持其导热性,同时通过数据采集卡进行温度监控,用以衡量焊点在通电情况下的实际温度。待电压、温度在数据采集卡中显示的数值稳定3 min后开始记录,当电压相对初始值增加10%时,将电源关闭,并将试样缓慢冷却至室温后取出。利用SEM扫描电镜,对该批次正交试验结果进行统计分析,研究焊点在不同工况条件下失效时的微观结构特征。

图2 BGA结构试验试样Fig.2 BGA test specimen

1.3 试验结果及分析

经过对试样多个工序的后处理,比如切割、打磨、抛光等,样品对应的失效焊点可以在SEM工具的帮助下观察到其微观结构特征。图3(a)和(b)分别是样品在150℃,电流密度为1.9×108A/m2和1.4×108A/m2条件下的微观结构形貌图。从图3(a)中可以看到,左右焊点的Cu焊盘均已消耗殆尽,并且大部分的焊点材料转变为了IMC。而当试样在同样的环境温度下承受电流密度为1.4×108A/m2时,右侧焊点与1.9×108A/m2条件下的结果一致,焊盘也已完全消耗,如图3(b)所示。因此右侧焊点,也就是电子流入侧的焊点是导致结构失效的主要原因。这是因为这部分区域由于存在较强的电流拥挤现象,从而导致该区域拥有更高的电流密度,而较高的电流密度会促进电迁移现象。同时,右侧焊点是电子流入的一侧,在电流拥挤区域中,较大的原子迁出速度使得互连引线中的原子不能及时获得补充,因而会发生失效。与之相对的是,虽然左侧焊点也存在电流拥挤效应,然而该侧是电子流出一侧,互连结构中的原子不断向左侧焊点迁移,使左侧焊点迁出的原子不断得到补充而保持较好的稳定性。

图3 150℃条件下电流密度为1.9×108A/m2(a);1.4×108A/m2(b)的微观结构形貌Fig.3 Microstructure morphologies at 150℃under 1.9×108A/m2(a)and 1.4×108A/m2(b)

而从另一方面考虑,图3(a)中左侧焊点已完全消耗,图3(b)中左侧焊点却变化较少,尤其是该焊点的焊盘几乎没有任何变化。电流密度的差异或许是导致该现象的原因。然而电流密度引起的电迁移现象是原子从阴极迁移至阳极,这并不能解释图3(a)中阳极焊盘的消耗。考虑到较高温度下焊盘中活跃的Cu原子更容易接受由焊点中迁移来的Sn原子,并与之结合形成不同的IMC,所以温度也会导致上述两种不同失效模式。因此本文取120℃,用同样的电流密度与之对比,如图4所示。

从图4中可以发现,在120℃恒温条件,电流密度为1.9×108A/m2及1.4×108A/m2条件下的电迁移失效模式均为裂纹扩展所主导。裂纹主要集中在阴极,并沿着焊接界面逐渐扩展而最终导致试样完全失效。通过对焊盘附近IMC的观察,由于仅有少量IMC生成,其对焊点失效的影响可以忽略。很显然,较低的环境温度会不利于原子的迁移,并且使原子始终处于临界状态以下而不利于IMC的生成。在这种条件下,迁移出去的原子会促使Kirkendall孔洞在阴极出现,进而使应力在孔洞周围集中而最终导致裂纹的萌生与扩展。

图4 120℃条件下电流密度为1.9×108A/m2(a);1.4×108A/m2(b)的微观结构形貌Fig.4 Microstructure morphologyies at 120℃under 1.9×108A/m2(a)and 1.4×108A/m2(b)

从上述结果可以发现,原子迁移的剧烈程度直接影响到BGA结构的电迁移失效模式。在较高的温度条件下,金属原子会比在较低温度的条件下更加活跃,因而更容易发生原子的迁移,这加速了IMC的生成,并随着焊点底部Cu焊盘的大量消耗而导致了整个互连电路的失效。与之相对的是,当互连电路处于一个较低的温度时,原子的迁移现象并不显著,其阻碍了IMC的形成,这种条件下的电迁移现象十分缓慢,特别是焊盘中的Cu原子的迁移,因此Cu的消耗速度低于其他原子的迁移速度,这是导致在焊接界面出现裂纹的主要原因。

2 数值模拟及寿命预测

2.1 原子密度积分法

通过试验对电迁移现象的研究通常需要花费大量的时间,然而基于数值模拟技术,可以通过多物理场耦合模拟得到电流密度、温度梯度和机械应力在结构内部的分布,利用有效的电迁移理论体系,对电迁移现象进行分析。

互连焊点中原子密度的演化方程是典型的质量守恒方程,表达式如下:

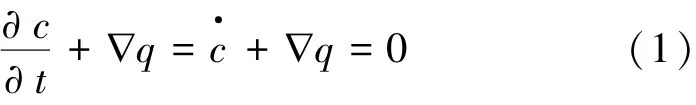
式中:c=C/C0为正则化的原子密度(C为实际原子密度,C0为无应力状态下初始原子密度);t为时间;q为正则化的原子迁移总通量矢量,主要由电子风力、温度梯度、应力梯度和原子密度梯度等驱动机制引起,其表达式为:

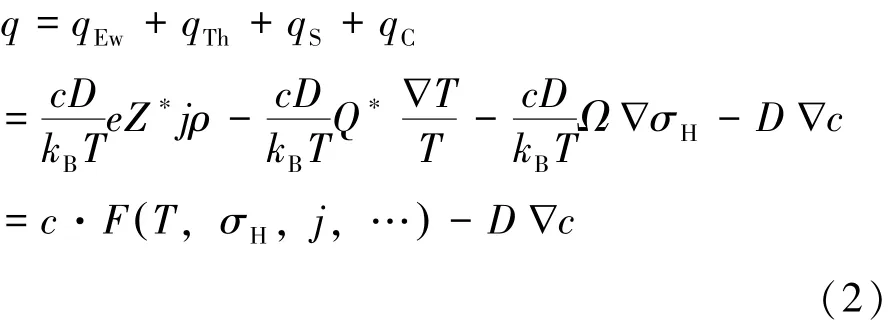
式中:kB为Boltzmann常数;e为电子电荷;Z∗为有效电荷数;T为绝对温度;Q∗为传输热,ρ为与温度相关的电阻率;σH为静水应力;j为电流密度矢量;为有效扩散速率;D0为初始扩散系数;EA为激活能;Ω为原子体积。

通常,在金属互连的边界Γ上,电迁移演化方程的边界条件可表示为

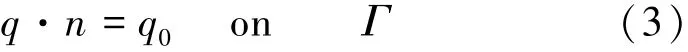
初始条件为所有节点的初始正则化原子密度

由电迁移演化方程和上述的边界条件、初始条件构成了电迁移原子输运的边界值问题。为此,基于伽辽金方法,引入权函数w,在封闭域V内对式(1)进行积分,并化简可得:式中,取权函数w=ψi(ψi是单元的形函数)。假设,进行单元的离散化,得到方程(6)的矩阵形式:

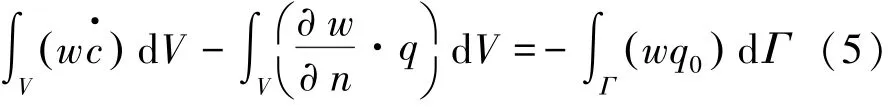
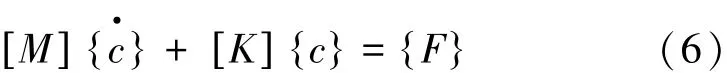
式中: [M]为与时间无关的质量矩阵; [K]为依赖于电流密度j、温度和静水应力σH等参数的刚度矩阵;{F}为已知项。

引入α族差分格式求解上式,忽略中间推导过程可得:

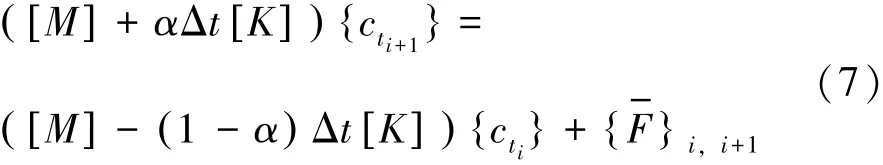
由于已知原子密度的初值c0=1,根据式(7)可以求得任意时间步的原子密度变化。

不同于传统的原子通量散度法,原子密度积分法不仅考虑了原子密度梯度这一驱动机制,而且满足质量守恒条件。原子密度积分法的详细计算过程见文献 [7-8]。

根据Sasagawa的试验结果[9],Al(1%Si)线的电迁移最小临界原子密度cmin=0.95,原子密度小于该最小临界原子密度时将形成空洞。对于无铅焊料,该临界值为0.85[10]。本文假设当单元的平均原子密度低于临界值时,该单元随即丧失导电性能。

2.2 有限元建模及材料参数

对于上文所应用的BGA结构,本文根据扫描电镜观察到的芯片内部详细构造,建立了简化的有限元模型,如图5所示。

图5 BGA试样内部构造(a)和有限元模型(b)Fig.5 Details of BGA structure(a)and FEA model(b)

试样所对应的材料参数列于表1[8];其中由于焊点采用SAC305焊料,其具有明显的黏塑性材料属性,因此本文使用ANAND黏塑性本构方程来描述焊点材料的力学行为,其ANAND本构模型参数如表2所示[11]。

表1 测试结构的材料属性Tab.1 Material parameters of test specimen

表2 SAC305的ANAND本构方程参数Tab.2 ANAND parameters of SAC305

2.3 有限元模拟结果及讨论

通过上文中介绍的模拟方法,利用本文介绍的算法对试验中的BGA结构进行电迁移有限元仿真。得到综合考虑四种电迁移驱动机制下焊点在失效时的正则化原子密度分布。以120℃,1.9×108A/m2为例,如图6所示。

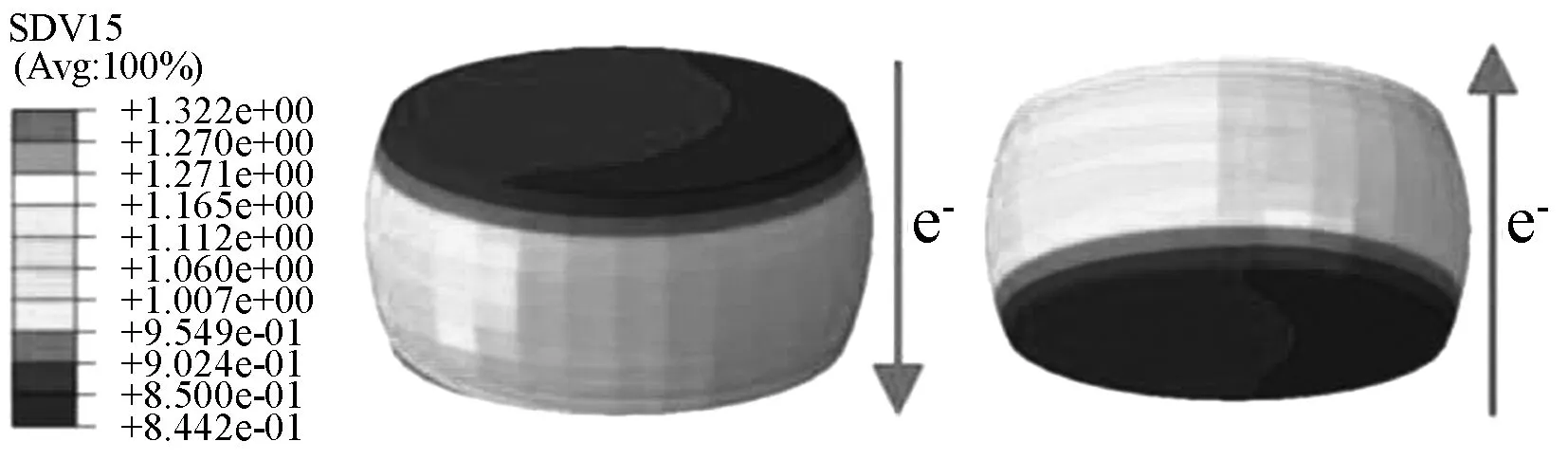
图6 电阻升高10%时焊点的正则化原子密度分布Fig.6 Atomic density distribution when the resistance raised 10%

从图6中可以发现,随着时间的推移,电子流入处的正则化原子密度逐渐减小,而阳极的正则化原子密度逐渐增大。由于本文所研究焊球的电迁移最小临界原子密度为0.85,原子密度低于临界值的区域则会出现由空洞引起的材料破坏。因此,空洞容易在电子流入口处形成,并逐渐横穿整个焊接界面,这与试验结果吻合。

随着焊点各处原子密度的不断变化,电流密度的分布也会发生较大改变,特别是形成空洞的区域均位于发生电流拥挤的位置,这会使电流拥挤区不断移动而造成界面内部拥有更高的电流密度。

图7(b)是发生电迁移失效时的电流密度分布结果,对比图6可以发现,由于每个焊点电子流入处的原子密度低于临界值,使该区域的导电能力大大下降,因而电流会优先从原子密度高的区域通过。这导致了电流拥挤区不断向界面中心移动,同时导电面积逐渐减少使得每个焊点的最大电流密度逐渐增加。在发生电迁移失效时,焊点的最大电流密度为5.57×108A/m2,而初始状态下的最大电流密度为3.67×108A/m2,如图7(a)所示,因此较大的电流密度会使原子的迁移随着电流拥挤区的逐渐移动而变得更快。

图7 初始电流密度分布(a);电阻升高10%时的电流密度分布(b)Fig.7 Initial current density distribution(a);current density distribution when the resistance raised 10%(b)

为了分析电迁移算法对两种失效模式进行描述的能力,本文针对上文试验中所使用的其他加载条件下的电迁移失效行为进行了模拟,并对比了4种条件下的电迁移寿命模拟结果以及试验结果,如图8所示。可以发现本文算法对120℃条件下的电迁移寿命有更精确的预测结果,而对于150℃条件下的电迁移现象,模拟得到的电迁移寿命与试验得到的结果差异较大。这是因为在150℃条件下,焊盘会有很大消耗,同时伴随有大量IMC的生成,这会使焊点的抗电迁移性能发生改变,体现在有限元仿真中则是电迁移参数的变化以及微观结构变化的影响,而目前的电迁移理论无法对其进行合理的考虑,因此试验中的电迁移寿命会与模拟结果有较大出入。

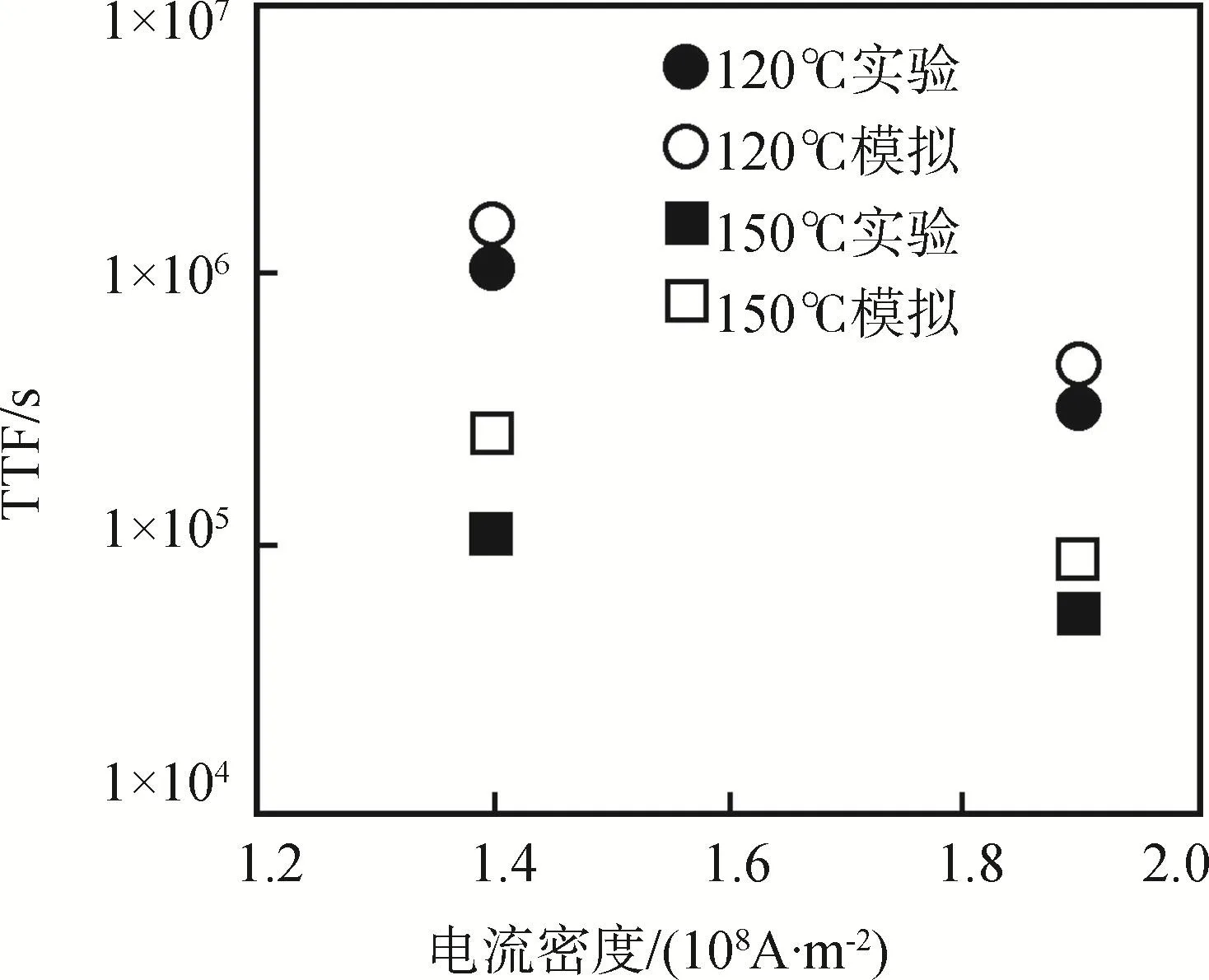
图8 四种载荷条件下的电迁移寿命(试验及模拟结果对比)Fig.8 Comparison between electromigration test and simulation result under four different loading conditions

3 结论

本文通过在不同电流密度及温度的条件下对BGA结构进行电迁移加速试验,进而对造成电迁移不同失效模式的微观机理进行了分析。结果表明由原子的显著迁移与裂纹扩展所主导的电迁移失效模式存在明显的竞争关系。当原子发生显著迁移时,伴随着IMC的大量生成,焊盘会有很大消耗;而当原子的迁移速度并不明显时,微孔洞的聚合在机械载荷的作用下则更易造成裂纹的萌生与扩展。同时通过原子密度积分算法对电迁移现象的研究会更适用于裂纹的扩展所引起的失效,这是由于原子的显著迁移造成了焊点内部组分的变化,而目前的电迁移理论并没有考虑该条件下材料性能的变化,因此在此基础上对电迁移理论进行修正很有必要。