PSR J0905-5127的计时噪声分析

周世奇，张 洁，袁建平，刘门全，朱晓丹，冯中文

(1.西华师范大学 物理与空间科学学院，四川 南充 637009；2.中国科学院 新疆天文台，新疆 乌鲁木齐 830001； 3.中国科学院大学 天文与空间科学学院，北京 100049)

0 引 言

脉冲星是二十世纪六十年代天文学的四大发现之一。观测上，脉冲星计时是研究脉冲星的重要手段之一。其本质上是把定期追踪到的射电脉冲信号的到达时间(Times of Arrival，TOAs)与理论预估的时间作对比，从而检测脉冲星自转行为以及演化[1]。然而，长期的观测研究发现，脉冲星的到达时间并不能被自转减慢模型理论所很好的预测；表现为两种主要的观测不稳定性，一种是周期跃变，另外一种是计时噪声[2]。周期跃变表现为自转周期短时间内(通常是几分钟)的大幅度跳跃(Δv/v～(10-6～10-9))和跃变之后时间跨度为几个月到几年不等的缓慢恢复过程；而计时噪声是指自转频率的随机游走(Δv/v<10-9)，时间跨度通常为几天、几个月和几年不等[3]。绝大多数脉冲星都具有计时噪声；而且对于年轻的脉冲星而言，计时噪声被认为是大幅度周期跃变的恢复过程所主导[4]。理论认为，计时噪声是中子星内部结构发生变化所造成的自转频率的扰动，所以对于计时噪声的研究有利于理解中子星内部。

1 数据来源

澳大利亚64 m帕克斯望远镜对射电脉冲星的计时观测和离线数据处理详见文献[4]。本文对使用的帕克斯望远镜对PSR J0905-5127在2007年7月(MJD—54302)至2014年4月(MJD—56747)的计时观测数据进行简要的说明。对这颗脉冲星大约每2～4周观测一次，观测的中心数据频率为1 369 MHz即20 cm波段，接收机的带宽为256 MHz的多波束接收机，后端系统采用的是数字消色散系统PDFB 1/2/3/4，积分时间为1～3分钟。数据可从Parkes Pulsar Data Archive[6]中下载。用脉冲星数据分析软件PSRCHIVE对原始数据进行消色散，之后得到每次观测的总强度轮廓。为了得到脉冲到达时间我们将每次的观测的轮廓与信噪比最高的好的脉冲轮廓做相关，然后将脉冲到达时间通过TEMPO2[7]程序中的Jet Propulsion Laboratories(JPL)的DE405星历表转换到太阳系的质心[8]。最后将得到TOAs用TEMPO2与模型通过相位相连来拟合得到计时残差。

2 分析方法

理论认为脉冲星通过偶极磁场辐射而损失能量，导致脉冲星自转会逐渐减慢。假设脉冲星所有的转动能量损失都是由于真空中偶极磁场辐射引起的。然而，也有可能存在其他原因使脉冲星损失能量。所以，对于更一般的情况，其角速度的变化与角速度的幂律成比例[9]，我们可以得到：

(1)

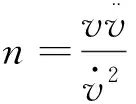
(2)

其中，K为常数，n被称为脉冲星的制动指数。如果我们对脉冲星进行长时间的计时观测，便可以得到其自转频率的一阶导数和二阶导数，进而得到制动指数。在磁偶极制动模型下，其制动指数n=3。因此制动指数是否等于3是判断脉冲星计时噪声的重要特征。到目前为止，长时间的计时观测表明只有六个脉冲星具有稳定的制动指数；绝大部分脉冲星的制动指数均因不同程度的自转不稳定性而偏离3。

从频域的角度来看，计时噪声包含两个成分：一个是平谱(或“白”成分)即高频成分，通常称为白噪声，一般认为由接收机噪声引起；另一个是陡谱(或“红”成分)即低频成分，也称为红噪声，通常认为是由自转周期内秉的不规则性引起[10]。大量观测数据显示，红噪声在年轻脉冲星的到达时间残差中占主导地位。造成到达时间噪声的因素有很多，有与脉冲星内秉性质相关的，如自转周期自身的扰动、跃变，脉冲轮廓的变化；也有脉冲星外部环境的扰动导致的，如引力波辐射、加速活动的球状星团、伴星的轨道运动；太阳系星历表的误差、时钟误差、定标误差等也会使到达时间无法准确预测。在随机游走模型下，红噪声主要由位相噪声(PN)、自转频率噪声(FN)和自转减慢率噪声(SN)三种所引起的[1]。

一般使用Cholesky方法[11]对计时噪声进行分析，基本原理是使用由残差的协方差矩阵得到的线性变换来白化残差和时间模型。脉冲星计时噪声的低频通常是幂律谱，而高频是白噪声。我们可以用低通滤波器分开低频和高频。低频常是过采样，可以被内插到规则网格而只有较小偏差；高频不能内插，但它们是白噪声，没有频谱泄露的影响，可以使用最小二乘方法。这样，我们可以组成一个复合谱，通过低通滤波器分谱，将两部分用不同的方法分析。

3 结 果

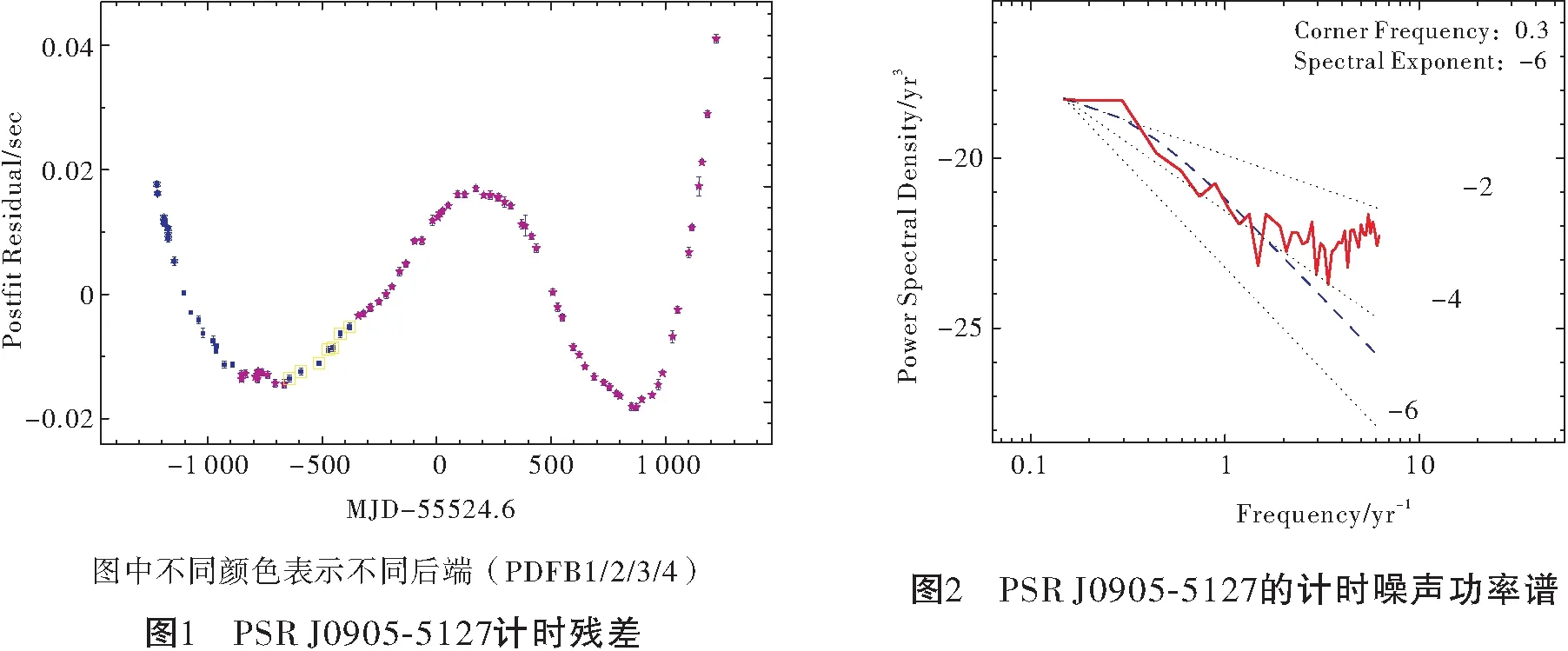
表1 脉冲星PSR J0905-5127的计时参数

Parameters ValuesRAJ09∶05∶51.9393424(0.04)DECJ-51∶27∶53.97995(0.38)Pulse frequency,v(s-1)2.88765680447(6)First derivation of pulse frequency,v·(10-12·s-2)-0.207207 (2)Second derivation of pulse frequency,v··(10-25·s-3)2(1)Post-fit residual(ms)12.464

注：第二列括号内的数值为TEMPO2给出的最后一位数的误差