钢-混凝土组合梁在简谐荷载下的动力响应试验研究
, ,
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.中铁建安工程设计院有限公司,河北 石家庄 050043)
0 引言
钢-混凝土组合梁通过抗剪连接件将钢梁和混凝土板结合在一起共同工作,可将其看作由混凝土板、连接件和钢梁一起组成的一种多构件的组合体系,在动力荷载作用下,混凝土板和钢梁通过连接件相互传递内力,共同变形,形成一个动力耦合系统。目前,国内外关于混凝土-连接件-钢梁动力相互作用系统的研究已有一些成果,主要是通过理论模型或有限元方法进行分析[1-6]。在动力模型试验方面,组合梁的自振特性试验有部分相关报道[7],但对于强迫振动下的动力响应,只有少量模型试验[8],主要是现场实测数据[9-10],无法进行参数分析。
在工程实际中,组合梁受到的强迫振动主要包括两种:一种是工业厂房中的组合梁受到机器振动的作用;另一种是组合梁桥受到移动车辆荷载的振动作用。由于移动荷载在试验室中不宜精确模拟,拟通过对组合梁模型在试验室内施加持续的简谐荷载,研究组合梁在强迫振动下的动力响应,得到组合梁动力试验的基本现象,明确连接件抗剪刚度对组合梁动力特性的影响,为组合梁的设计和计算提供理论依据。简谐荷载下的动力响应同样能反映移动荷载下组合梁的动力特性。
1 试验设计及加载方案
1.1 试验目的及内容
测试简谐正弦荷载下组合梁的动力响应,包括跨中加速度时程、梁两端的滑移时程及梁跨中的竖向挠度时程;分析连接件抗剪刚度(剪力连接度)及简谐荷载特性对组合梁动力特性的影响。
1.2 试验设计与制作
以剪力连接度为参数,共设计3片模型梁,箱型截面,简支跨度6 000 mm,梁全长6 200 mm,混凝土板长6 200 mm,宽700 mm,厚70 mm;钢梁高180 mm,下翼缘宽430 mm,翼缘板厚8 mm,腹板厚8 mm;栓钉直径13 mm,高50 mm。钢梁采用Q235钢,混凝土C30,钢筋一级钢筋,横隔板均为5片,间隔1.5 m。
试验梁SCB1,剪力连接度为1.1,在钢梁每侧腹板上翼缘上布置单列栓钉41个,纵向间距150 mm,两侧栓钉共82个;SCB2剪力连接度为0.67,在钢梁每侧腹板上翼缘上布置单列栓钉25个,纵向间距250 mm,两侧栓钉共50个;SCB3剪力连接度为0.43,在钢梁每侧腹板上翼缘上布置单列栓钉16个,纵向间距400 mm,两侧栓钉共32个。
各试验梁参数见表1,各试验梁截面尺寸以及栓钉布置的具体间距见图1。图中,横隔板只在各纵剖面图中显示;混凝土板只在横截面图中显示。

表1 试验梁参数
注:表1中各试验梁横隔板分别设置在两个梁端支座、跨中和两个1/4跨度处。

图1 试验梁截面尺寸及布置详图(单位:mm)
1.3 试验装置及加载方案
试验装置包括1 000 kN三维协调电液伺服动态加载试验系统、竖向加速度测量装置(东方所941B型竖向拾振器、滑移和挠度测量装置(高感度变位计CDP-10)、加速度采集装置(东方所16通道(3018C)采集仪、941型八线放大器)、滑移及挠度采集装置(SA-8动态应变仪)。
试验梁为简支结构,一端为固定支座,一端为活动支座。分别在梁的跨中、2L/3处、3L/4处进行简谐荷载重复加载。简谐荷载可表示为
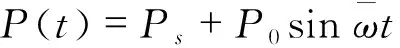
(1)
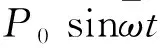
以静态荷载分量、简谐荷载幅值和频率为参数设置7种工况,见表2。其中工况1、5、6研究静载分量和荷载频率相同时,加载幅值对组合梁动力响应的影响;工况2、5、7研究简谐荷载频率和幅值相同时,静载分量的影响;工况3、4、5研究静载分量和加载幅值相同时,简谐荷载频率的影响。试验梁加载布置图见图2。
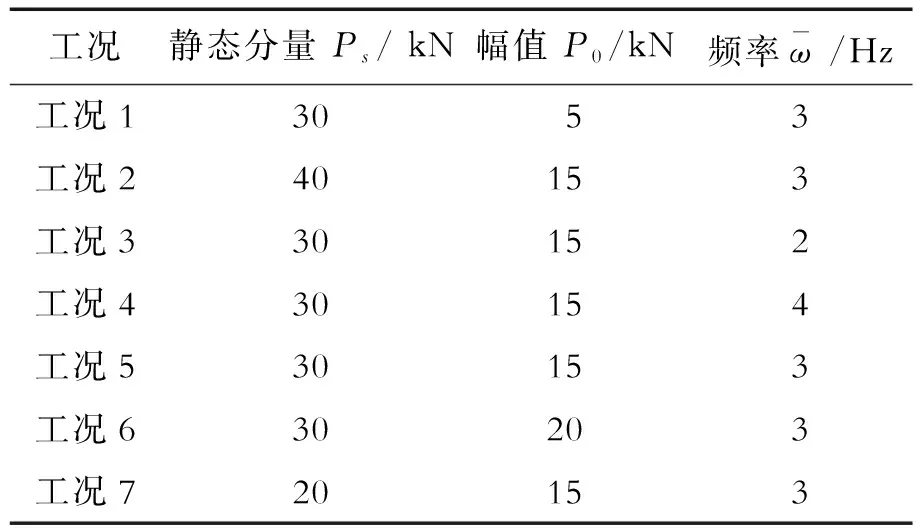
表2 简谐荷载加载工况

图2 加载布置图
首先进行预加载,测试试验梁性能,并消除钢梁与混凝土板之间粘结力的影响。为测试梁跨中加速度响应,在梁跨中,靠近加载头两边均放置一个竖向拾振器,档位选择1档,即加速度档。跨中、2L/3处及3L/4处加载时的滑移测点布置见图3。
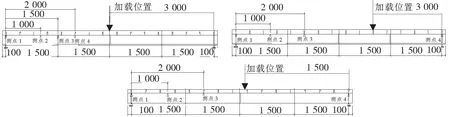
图3 加载位置及滑移测点布置图(单位:mm)
2 测试结果分析
2.1 持续简谐荷载作用下组合梁的动力响应测试结果
各试验梁在不同加载位置,在各工况下的跨中加速度时程、跨中挠度时程及各测点滑移时程在简谐荷载下均表现出简谐变化的波动形式,只是数值不同。下面以试验梁SCB3的工况4(静载分量30 kN、加载幅值15 kN、频率5 Hz)为例,给出跨中简谐荷载作用下的动力响应,见图4。试验中所有时程分析均在50 Hz低通滤波下进行。
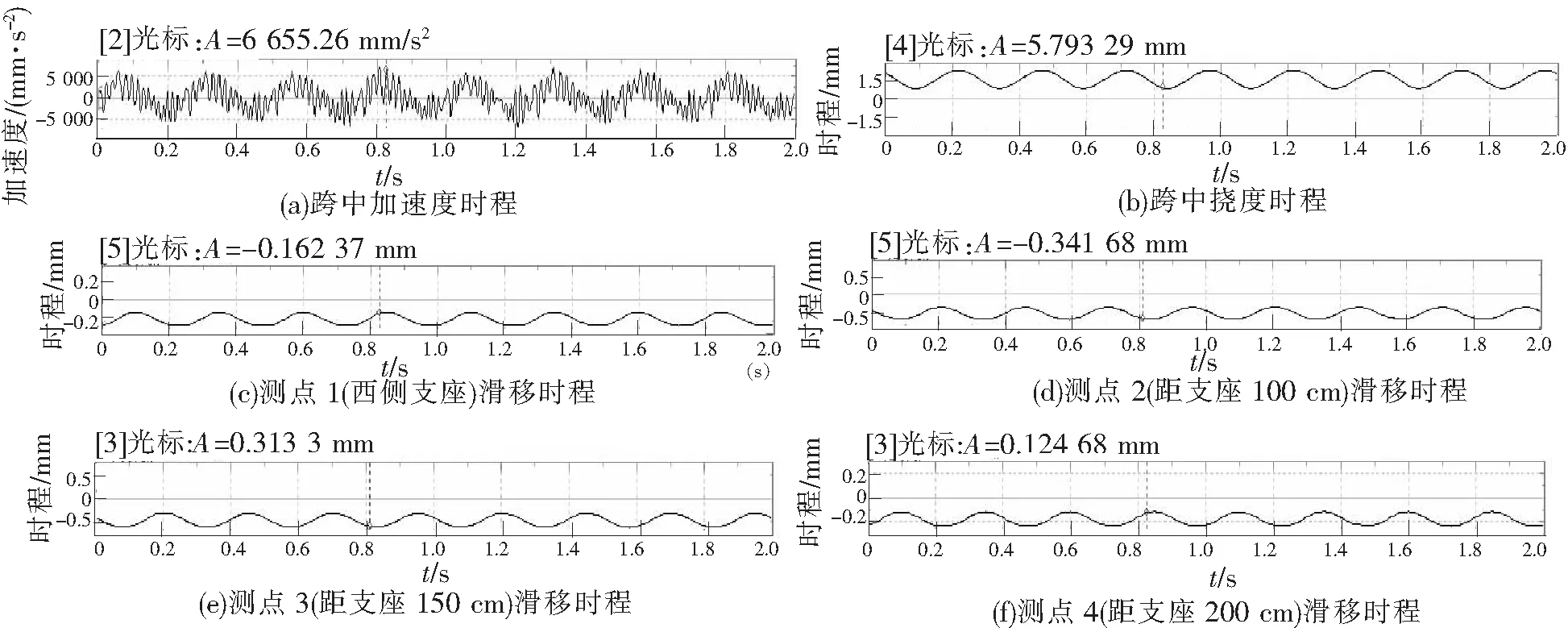
图4 加载工况4组合梁的动力响应
由图4可知:在加载过程中,试验梁在正弦荷载下的动力响应均随时间表现出正弦波的变化形式,SCB3梁在工况4下的跨中加速度最大值为6 580.3 mm/s2;跨中挠度最大值为9.004 mm;测点1滑移均值0.172 mm,幅值0.131 mm;测点2滑移均值为0.209 mm;测点3滑移均值为0.191 mm;测点4滑移均值为0.141 mm。可以看出滑移均值并非支点处最大,而是靠近支点的测点1(距支座100 mm)最大,其后测点3、4的滑移均值则随其远离支座的距离逐渐减小,其它试验梁和其它工况的测试结果也表现出相同的趋势。
2.2 剪力连接度对组合梁动力响应的影响
2.2.1 剪力连接度对结合面相对滑移的影响
图5、图6分别为相同截面、跨度,不同剪力连接度的3根试验梁在不同加载位置、不同工况下梁端滑移均值和滑移幅值的对比。
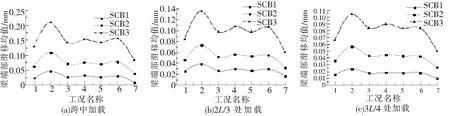
图5 剪力连接度对试验梁梁端滑移均值的影响
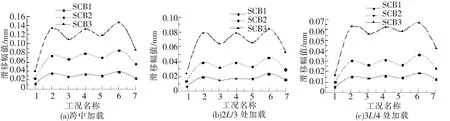
图6 剪力连接度对试验梁梁端滑移幅值的影响
由图5、图6可知:
(1)在不同加载位置,不同工况下,滑移均值和幅值均随着组合梁剪力连接度的降低而增大。
(2)连接度相同时,对于滑移均值,静载分量最大的工况2下最大,最小的工况7下最小,其余工况下则基本相同,说明其主要受静态荷载分量影响,受简谐荷载幅值和频率的影响很小。
(3)连接度相同时,对于滑移幅值,荷载幅值最小的工况1下最小,最大的工况6下最大,其余工况基本相同,说明滑移幅值主要受荷载幅值的影响,受静载分量和荷载频率的影响较小。
2.2.2 剪力连接度对跨中加速度的影响
图7为相同截面、跨度,不同剪力连接度的3根试验梁在不同加载位置、不同工况下的跨中加速度对比。
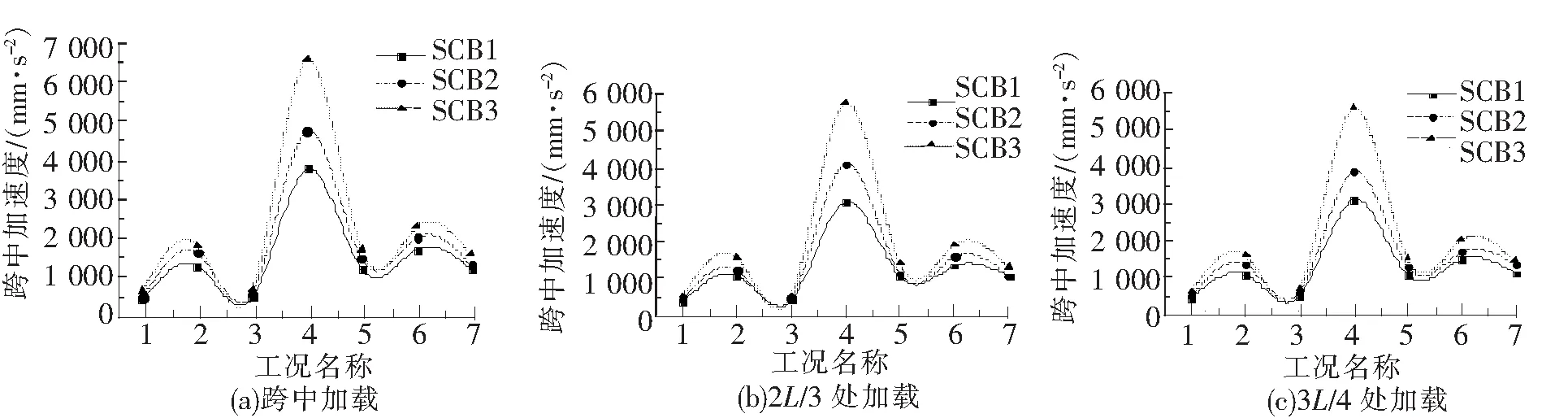
图7 剪力连接度对试验梁跨中加速度的影响
由图7可看出:
(1)在不同加载位置,不同工况下,试验梁跨中加速度均随着组合梁剪力连接度的降低而增大。
(2)连接度相同时,荷载频率最大的工况4下,跨中加速度值最大;荷载频率相同的工况2、5、6、7下,跨中加速度值基本相同;工况1和工况3下的跨中加速度最小,其中工况3的荷载频率较其它工况都小,工况1的荷载频率虽然与工况1~2、5~7相同,但荷载幅值最小,说明跨中加速度主要受荷载频率和荷载幅值的影响,受静载分量的影响相对较小。
2.2.3 剪力连接度对跨中动挠度的影响
图8为相同截面、跨度,不同剪力连接度的3根试验梁在不同加载位置、不同工况下的跨中动挠度对比。
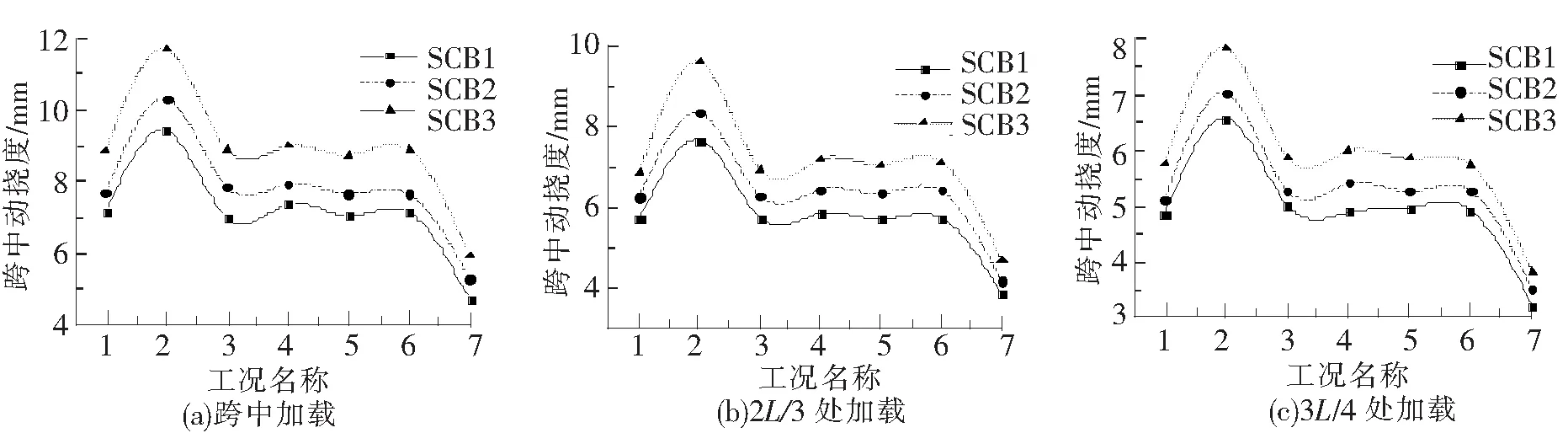
图8 剪力连接度对试验梁跨中动挠度的影响
由图8可看出:
(1)在不同加载位置,不同工况下,试验梁跨中动挠度均随着组合梁剪力连接度的降低而增大,说明其抗弯刚度下降。
(2)连接度相同时,静载分量最大的工况2下,跨中动挠度最大,工况7下跨中动挠度最小,其余工况下则基本相同,说明跨中动挠度主要受静态荷载分量影响,受简谐荷载幅值和频率的影响很小。
2.3 荷载参数对组合梁动力响应的影响
2.3.1 静载分量的影响
图9为试验梁在动态分量及加载频率相同,静态分量不同的简谐荷载下的动力响应,即对工况2、5、7(静载分量分别为40 kN、30 kN、20 kN)的加载结果进行分析。

图9 简谐荷载静态分量对组合梁动力特性的影响(工况2、5、7)
由图9可知:
(1)在相同幅值和加载频率的情况下,跨中挠度、滑移均值与所加静态荷载分量大小成正比。
(2) 理论上滑移幅值应不受静态荷载分量的影响,但图9(d)显示,随静态分量的减小,滑移幅值有所降低,但变化幅度不大。究其原因,是因为随荷载幅值的不同,上下限荷载值也发生变化,而荷载与滑移并非线性,而是非线性关系,因此滑移幅值也会产生一定的影响。
(3)加速度随静载分量的变化很小,只在剪力连接度最小的SCB3中随静载分量表现了一定的下降趋势。
综上可见,荷载的静态分量主要对组合梁的跨中挠度及滑移均值有影响。
2.3.2 简谐荷载幅值的影响
图10为试验梁在静态分量及加载频率相同,幅值不同的简谐荷载下的动力响应,即对工况1、5、6(加载幅值分别为5 kN、15 kN、20 kN)的加载结果进行分析。
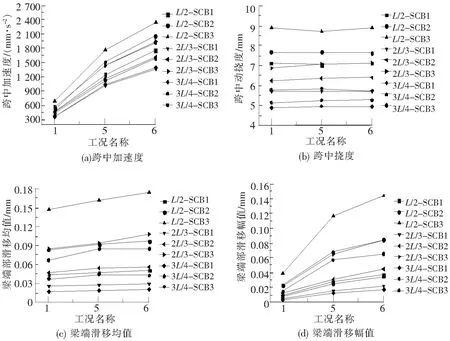
图10 简谐荷载幅值对组合梁动力特性的影响(工况1、5、6)
由图10可知:当静载分量和荷载频率相同时,随加载幅值的增大,试验梁的跨中动挠度和梁端滑移均值均变化不大,跨中加速度和梁端滑移幅值则显著增加,但并不是线性增加的关系,而是表现出一定的非线性。
2.3.3 简谐荷载频率的影响
图11为组合梁在静态分量及动态幅值相同、加载频率不同的简谐荷载下的动力响应,即对工况3、5、4(加载频率分别为2 Hz、3 Hz、4 Hz)的加载结果进行分析。
由图11可知,静载分量和加载幅值相同时,随简谐荷载频率的增大,跨中加速度增加明显,但跨中竖向挠度及组合梁的滑移所受影响不大。
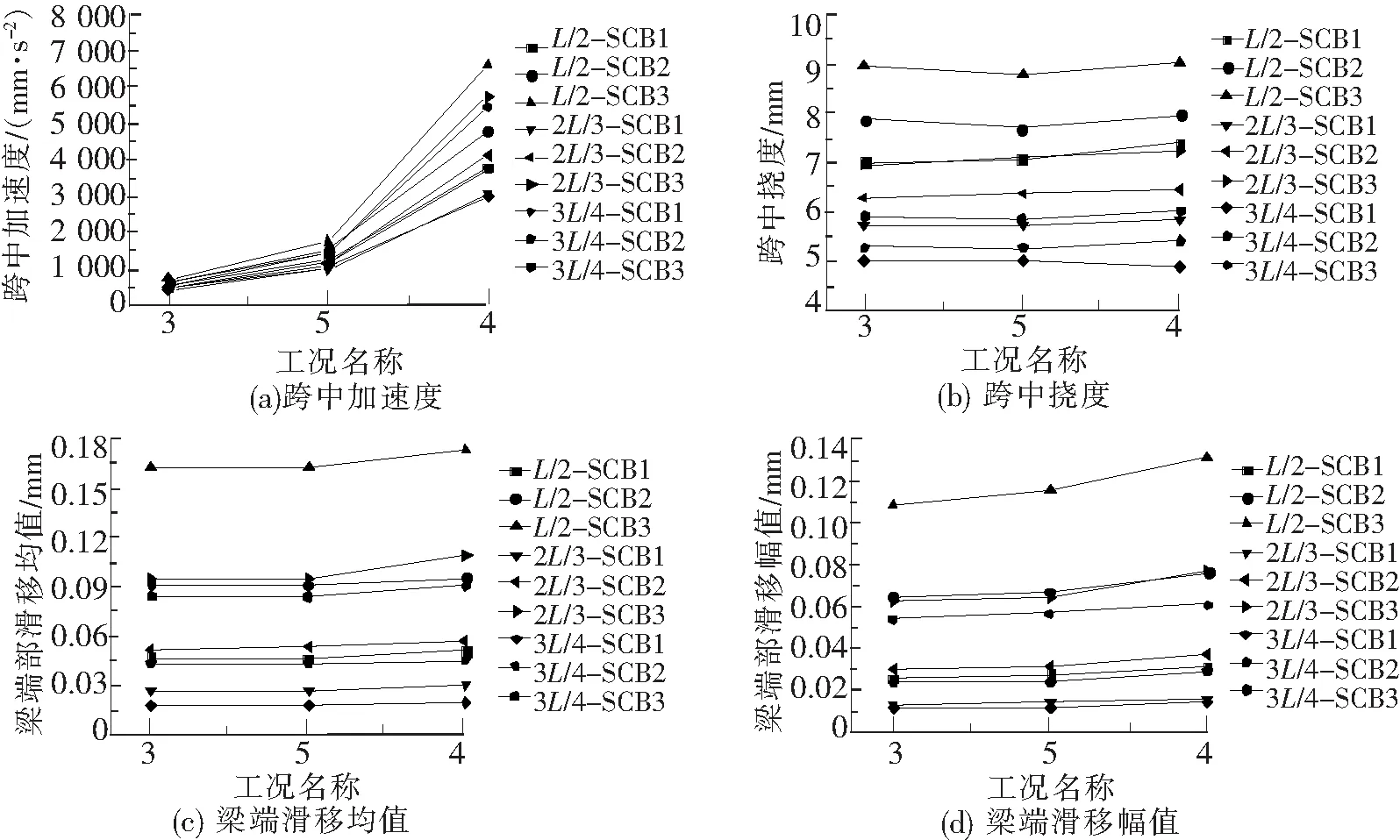
图11 简谐荷载频率对组合梁动力特性的影响(工况3、5、4)
3 结语
以剪力连接度为参数设计了3片钢-混凝土简支组合梁,进行简谐荷载下的动力相应试验,测试了其跨中动挠度、跨中加速度和结合面滑移,结果表明:
(1)各试验梁在不同加载位置,在各工况下的跨中加速度时程、跨中挠度时程及各测点滑移时程在简谐荷载下均表现为随时间变化的波动形式。
(2)在不同加载位置,不同工况下,组合梁结合面的滑移均值和幅值、跨中加速度、以及跨中动挠度均随着剪力连接度的降低而增大,剪力连接度反映了组合梁结合面的抗剪能力,随连接度的减小,梁的整体抗弯刚度下降。
(3)组合梁跨中动挠度和结合面滑移均值均主要受静态荷载分量影响,受简谐荷载幅值和频率的影响很小;滑移幅值主要受荷载幅值的影响,受静载分量和荷载频率的影响较小;跨中加速度主要受荷载频率和荷载幅值的影响,受静载分量的影响相对较小。

