地球定向参数的预报与应用研究

阚起源

引言：地球定向参数预报、地球定向参数应用等内容受激发源影响极易导致研究准确性降低，进而影响相关框架转换效果，并且，数据处理难度会逐渐加大，最终会延迟地球定向参数获取时间.从中能够看出，本文这一论题具有探究必要性和重要性，具体探究如下.

1 地球定向参数研究必要性

我国研究地球定向参数的时间相对较早，实际研究的过程中构建了时间参考系统，以便为论题分析提供支持.由于学者研究视域不断拓展、研究理论内容不断丰富，总结得知地球自转变化有规律可循，这为地球定向参数研究奠定了良好基础.以往研究设备主要为光学仪器，但该设备实际应用的过程中易受其他因素影响，进而会大大降低中观测准确性.后来相关研究技术不断升级，应用GPS技术、VLBI技术、DORIS技术研究地球定向参数，能够大大提高测量准确性，测量精度是以往的十倍，这意味着研究学者能够获得丰富的地球动力学信息，能为关联问题分析提供便利，有利于加快地球动力学发展步伐.

针对地球定向参数精确值深入探究，除了能够促进地球动力学发展，还能扩大其应用范围，我国航空航天事业定位准确性会大大提高.由于地球定向参数解算程序十分繁琐，并且数值获取时间较长，因此，应以地球定向参数预测为基础，掌握三天内定向参数数值，同时，建立预测模型，尽最大可能提高地球定向参数预测准确性.

2 地球定向参数研究进展及参数测定

2.1 研究进展

地球定向参数研究进展主要从两方面来分析，第一方面即是极移研究进展，第二方面即日长研究进展，其中，极移研究进展最早由德国学者提出，提出时间于十九世纪八十年代，研究可知，极移周期项包括长周期项、季节性摆动、线性趋势项、钱德勒摆动、高频变化项.极移激发源周期分量从时间尺度、季节性摆动、长期趋势、高频变化等方面来分析，各个方面依次对应的内容主要有可能的激发源；大气、地下水、海洋物质在分布；地壳反弹、冰川融化；大气、潮汐变化.日长研究进展研究内容细分为日长的长期变化、周期性变化、不规则变化、激发源等，其中，潮汐摩擦导致日长周期延长；周期性变化内容具体指的短周期变化、季节变化、周日变化；不规则变化具体指的是年际变化、高频不规则变化、十年尺度变化、年代际变化等.

2.2 参数测定

地球定向参数测定的过程中，既要选用适合的观测手段，又要合理排列地球定向参数数据序列.

地球定向参数测量技术更新换代的过程即大地测量技术发展的过程，最早应用的技术即甚长基线干涉技术，这一技术最早应用于天文学，在空间测量方面的精度相对较高，并且技术稳定性较强，甚长基线干涉技术实际应用时需要建立地球参考框架，在区域地壳形变监测、地球定向参数确定方面提供了技术支持.之后激光测卫技术被成功研制，该技术具有准确定位、高精度等优势，激光测卫技术适用于板块运动监测、自转参数确定.全球定位系统成功研制后，该系统通过发挥高精度、全天候等优势被广泛应用，上世纪九十年代成功建立全球定位系统连续观测网，并相继提供种类多样的数据产品.相对比而言，全球定位系统能够有效弥补上述两种技术存在的不足，预测可知，全球定位系统未来应用前景十分广阔.此外，DORIS技术应用监测时间相对较短，现有观测站接近60个，DORIS技术获取的数据信息利用IDS高效处理、具体分析，分析、处理后的数据在地球定向参数解算中发挥了重要作用[1].

国际地球自转服务组织针对地球定向参数变化时间序列权威发布，序列来源于数据综合结算操作，相对而言，序列准确性较高，序列内容包括IERSEOPC01、IERSEOPC04、IERSEOPC02/03.现 如今，模型构建、模型分析主要以EOPC04序列为基础，并据此衡量模型预测效果.

3 地球定向参数的预报及应用分析

3.1 时间序列法

3.1.1 数据处理

数据处理的过程中，利用IERSEOPC04这一序列分析定向参数值，通过极移时间完成预测.从日长角度来讲，应对数据预处理，处理过程功能中选用适合的计算方法，按照扣除固体潮、预测日长变化序列等步骤完成数据预处理任务.数据预处理工作执行时，参照IERS规范，应用日长影响计算公式，针对未知序列准确取值，通过公式代入求得固体地球带谐潮项值，并对比分析固体地球带谐潮项对日长的影响.大部分预测模型针对地球定向参数预测时首选组合预测方式，步骤主要为：利用最小二乘法完成拟合处理，拟合对象主要为地球定向参数序列周期项或者趋势项，之后进行外推预测；应用拟合残差法深层次预测，获取预测结果，拟合残差法能够直观显示中长期变化情况，能为长期预测奠定良好基础.由于不同时间段的精度预测要求存在差异，再加上，部分参数受外界因素影响较大，最终会出现异常现象，导致地球定向参数预测准确性大大降低[2].

3.1.2 构建RLS+ARIMA模型

ARMA模型构建：上世纪七十年代，西方学者通过模型组合的方式进行地球定向参数预测分析，参与组合的方式主要有回归模型、自回归滑动平均模型、移动平均模型.现如今，RLS+ARIMA模型构建后主要用于分析日长预报，对此，研究人员持差异化分析观点，部分研究人员持不同分析观点，其中，ARMA模型、AR模型均发挥过预测作用.相对比而言，本文介绍的RLS+ARIMA模型在关联性分析方面有重要意义.需要特别说明的是，ARMA模型能够满足序列平稳性需要，并且序列周期性特征明显，此时数据预处理的常用方法为差分法，该方法应用后构建完成的模型被称为ARIMA模型.在此期间，应在观察数据变化趋势图的基础上，依据数据完成函数判断任务.

模型识别：在模型分类、模型种类总结的基础上，总结时间序列特点，同时，对比分析时间序列以及模型序列在特点方面的异同，最终优选适合的模型.在这一过程中，需要应用自相关函数公式、偏相关函数公式完成不同模型数据数据特征的对比[3].

模型定阶：该环节参照FPE准则、AIC准则、BIC准则检验模型适用性.

模型参数估计：该环节应用的估计方法主要为Yule-Walker方法，其中，ARMA模型参数估计过程较繁琐，具体估计时，首先掌握该模型截尾特点，然后有序完成自回归参数估计工作，最后获取滑动平均参数，在这一过程中应用的函数主要有自协方差函数.

计算及分析：为避免预算量过大，适当减少模型阶数，同时，应用历元残差数据完成对获取数据结果的检验，最终获取极移坐标.针对模型合理性分析时，对比AR模型以及ARIMA模型，对比分析后选用相对合理的模型.分析可知，ARIMA模型实际应用的过程中，存在误差快速增长这一不足，因此，应探索有效措施予以处理.

3.2 神经网络法

3.2.1 神经网络概述

所谓神经网络法，指的是人工神经网络，该方法在信息分布式处理、存储等方面起到了重要作用，该方法优势主要表现为：鲁棒性、容错性，在非线性问题处理方面取得了具有实践指导作用的研究结果.神经网络法研究经历了不同阶段，其中，BP算法应用意味着神经网络正式用于实践，并且相关学者建立了神经网络模型[4].

神经网络细分不同类型，其中，径向基神经网络具有良好的局部优化性能，并且结构简单、学习用时短，它以径向基函数为基础，有步骤完成输入矢量变换，同时，在高维空间中完成数据交换，高效解决线性划分问题.径向基神经网络组成部分包括三方面，第一方面即输入层，第二方面即隐含层，第三方面即输出层，网络结果如图1所示.径向基神经网络借助高斯函数完成激励任务，径向基神经网络学习的过程中，应用到的参数主要有输出单元权值、RBF中心、方差.学习阶段细分为自主学习、监督学习，前者需要确定基函数方差，后者需要确定权值.

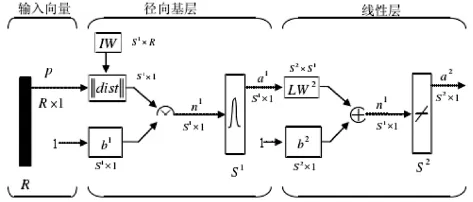
图1 径向基神经网络结构

3.2.2 EOP预测

总结已有分析内容可知，地球定向参数呈现非线性特点，神经网络方法显示较强的非线性逼近能力，与此同时，专业学者针对神经网络高度关注，并完成了定向参数的全面预测，预测内容包括地球定向参数、日长参数等.预测期间首先应用最小二乘法，然后应用神经网络法，以此提高神经网络预报分析效率.

EOP预测的过程中，应首先确定输入样本长度，合理设置输入、输出模式，这对神经网络预测效果有重要影响，如果输入样本长度过长，那么神经网络训练面临较大压力，适宜长度为10.然后，以RBF神经网络二次建模为基础完成EOP预测，借助神经网络完成对极移以及日长参数两方面的预报，与此同时，全面总结所获取观测值特点，利用模型完成特定时间段的预报，并记录预测残差，接下来进行二次预报，叠加第一次和第二次的预测结果，得到最终预测结果（如表1所示），最后，构建神经网络ARMA组合预测模型，遵循神经网络作函数模型构建、预测残差分析、预测残差随机模型构建这一原则，随着预测时间的延长，神经网络ARMA组合预测模型在预测误差补偿方面的优势逐渐突出，误差补偿精度相应提高[5].

表11 ms——5ms日长预测精度两次预测结果表

4 结论

综上所述，针对“地球定向参数的预报与应用”这一论题展开探究时，大致了解论题分析的必要性，并掌握地球定向参数研究进展，以及参数测定理论内容，应用时间序列法、神经网络法完成地球定向参数预报与应用分析任务.分析可知，短时预测无论是应用神经网络时间序列组合预测模型，还是应用RBF神经网络二次建模，均能获取的良好的预测效果.日长预测方法有待进一步分析，我国在日长预测方法探究方面有较大进步空间.