基于太沙基公式的地基极限承载力数值计算方法研究
陈元盛
(1.西安理工大学,陕西 西安 710048;2.陕西省引汉济渭工程建设有限公司,陕西 西安 710010)
1 研究背景
地基极限承载力是指地基在剪切破坏发展即将失稳时所能承受的极限荷载,亦称地基极限荷载。实际工程应用中,地基承载力的确定途径有两种,一是根据土的强度特性,结合地基破坏特点,用不同的理论方法进行计算;另一种是结合建筑经验和使用某些现场试验方法,以确定地基承载力。地基承载力的课题涉及面很广,影响因素较多,如土体材料和力学性质,基础尺寸,埋深等。为简化计算,多数理论计算公式中存在不符合实际的假设条件,而经验公式仅仅是一定程度的数学变换,缺乏理论支持,现场原位试验费时耗资,操作复杂,测试周期太长,测点随意性大,尺寸效应明显等,这些都是实际存在的问题。本文提出基于有限元理论,通过数值计算的方法确定地基承载力,可以一定程度地规避上述问题,节省时间和成本,为确定地基极限承载力提供理论支持和数据支撑。
2 参数折减法及地基安全系数
本文提出参数折减法与强度折减法在利用有限元计算分析边坡稳定性时的原理和操作过程基本相似。边坡稳定性分析中应用的有限元强度折减法的核心内容认为:边坡稳定系数是边坡刚好达到临界破坏状态时,对土的剪切强度进行折减的程度,稳定系数是边坡土体的实际剪切强度与临界破坏时折减后的剪切强度的比值。实际在进行有限元计算过程中,基于抗剪强度公式对强度参数粘聚力c和内摩擦角φ等比例折减,认为计算结果不收敛时的折减系数即为边坡稳定系数,该方法有明确的理论基础,为国内外专家学者认可。
本文中基于地基承载力的统一公式K.太沙基(Terzaghi)承载力公式。
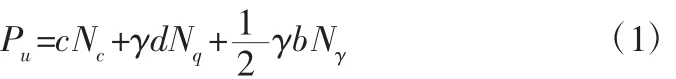
类似于强度折减法,可以发现与地基土的相关的参数c和γ具有一定的线性比例关系,在外荷载一定时,通过逐级等比例增大折减系数反复进行计算,达到计算模型的极限承载状态,此时的折减系数即为安全系数,而外荷载与折减系数的乘积即为地基极限承载力Pu,从而形成了一种新的应用于地基承载力数值计算的方法-参数折减法。
3 参数折减法原理及公式推导
现定义在外荷载保持不变的情况下,地基土体所能发挥的承载能力P与外荷载作用下土体内产生的实际承载力P'之比,即为地基承载力安全系数Fs。
具体公式推导过程如下:
由地基稳定安全系数的定义可以得到:
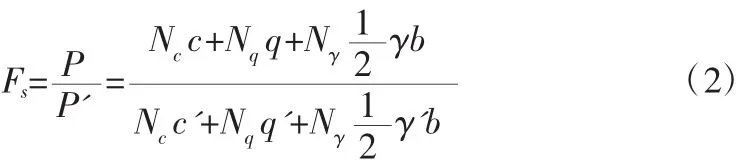
对式(1)两边同时除以Fs, 等式变形为:
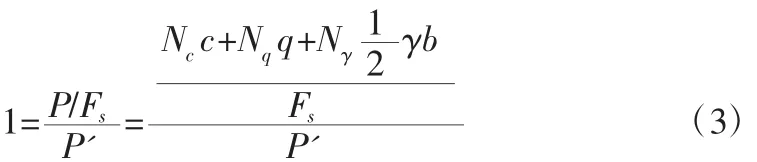
(2)式左边等于1表示地基所能发挥的承载力与实际承受的承载力相等,此时地基处于极限承载状态,而等式右边分子中需要对每一项除以Fs,由于q=γDf,在此处将Fs分配到地基土体的粘聚力c和γ容重上,如式(2)所示。
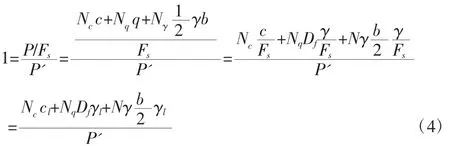
数学变换之后等式仍然成立,其中:

也可以表示为:

推导过程说明参数折减法有明确的数学理论支持,可以类似于强度折减法通过数值计算方法确定地基极限承载力和地基稳定安全系数,需要建立模型试算验证。
4 参数折减法数值仿真计算过程
4.1 计算模型、屈服准则
在有限元软件ANSYS平台上建立计算模型:三维均质黄土地基,模型尺寸300 m×180 m×50 m,共划分29516个单元,单元类型为solid45,四周采用法向固定边界,底部采用全方向约束,上边界为自由边界,采用弹-塑性模型,采用M-C屈服和强度准则。材料特性数据来源于西安地铁一号线洒金桥站土工试验报告 E=8e+6,μ=0.33,c=38000 kPa,φ=22°,D=2.01 g/m3;其次,在模型的顶部嵌入0.5 m埋深,1 m×1 m的混凝土方板作为载荷试验平板,E=9.52e+9,μ=0.20,D=2.50 g/m3。
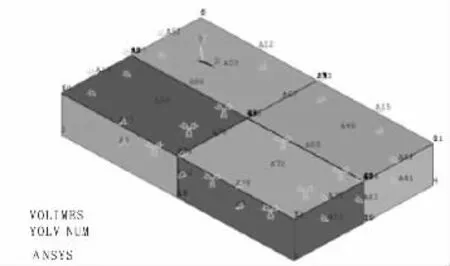
图1 地基基础模型三维视图
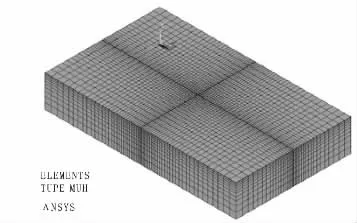
图2 网格剖分
4.2 数值计算过程、结果
基于ANSYS平台,按照塑性区域由基础边缘贯通至地表时,认为此时地基土体达到极限状态作为判据时,分别按照折减系数为 1.0,1.5,2.0,2.5,3.0 折减五次反复计算,每折减一次模型计算参数c和γ,从0开始逐级对载荷板加载,直至计算结果塑性区贯通,认为是此时模型地基条件的极限承载力F1.0,然后进行下一个折减系数下的逐级加载计算依次得到F1.5,F2.0,F2.5,F3.0。

表1 不同折减系数时的地基极限承载力 单位:Pa

图3 塑性区发展过程
5 数值计算结果正确性验证条件
现定义承载力比例系数Ki:对于某一土质地基计算模型,当极限状态判断准则确定时,地基土体材料未折减与每次折减后通过计算所确定的极限承载力之比,用公式表示为:

P0为不折减时土体极限承载力;
Pi为折减后土体极限承载力,i为折减系数标号,如折减系数为1.5和3.0时的极限承载力分别可以表示为:P1.5和P3.0,然而当折减系数为1.0时,P1.0=P0。
当折减系数与所对应的承载力比例系数相等即:

式(8)表明:如果将极限承载力比例系数和折减系数绘制成关系曲线,则在坐标系中表示为斜率为1的直线性关系,这说明了参数折减法是正确的。
5.1 塑性区贯通计算结果的正确性验证
绘制极限荷载~折减系数曲线(Pu~Fi)和极限荷载比例系数~折减系数(Ki~Fi)两种曲线。
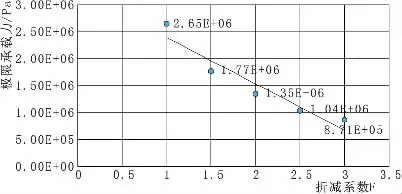
图4 极限承载力随折减系数的变化曲线
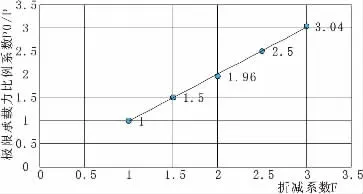
图5 折减系数与极限承载力比例系数的关系曲线

表2 不同折减系数时的极限承载力比例系数
分析图4变化曲线,可以看出随着折减系数的增大,极限荷载在减小,这是因为土体强度参数粘聚力c和γ材料参数同步得到折减,由太沙基公式 Pu=Ncc+Nqq+Nγγb/2 分析,当这两个参数等比例折减时,承载力应该是线性减小的。分析图5变化曲线可得极限承载力比例系数与折减系数之间基本上呈斜率为1的直线,通过原点的线性增长关系这说明对土体材料折减程度与极限荷载之间的折减程度相同,这是符合参数折减法的判断条件式(8)的。随后验证调整计算模型中某一参数时结算方法仍然正确。
5.2 调整载荷板尺寸计算结果的正确性验证
对2.1节计算模型中荷载试验平板尺寸扩大5倍,调整为5 m×5 m,其余参数和计算条件不变,进行折减计算并分别绘出Pu~Fi和 Ki~Fi曲线。
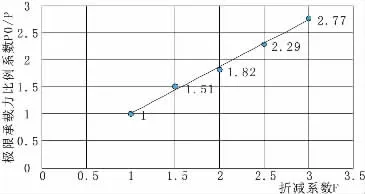
图6 极限荷载随折减系数的变化曲线(5 m×5 m)
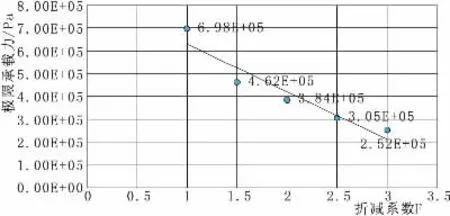
图7 折减系数与极限荷载比例系数的关系曲线(5 m×5 m)
图6 和图7满足随着折减系数的增大,极限荷载在减小和变化曲线可得极限承载力比例系数与折减系数之间基本上呈斜率为1的直线的验证条件。
5.3 调整土体压缩模量计算结果的正确性验证
对2.1节上述计算模型土地压缩模量(弹性模量)扩大100倍,其余参数和计算条件不变,再分别按照折减系数为1.0,1.5,2.0,2.5,3.0 折减五次反复计算,得到 F1.0,F1.5,F2.0,F2.5,F3.0和绘制极限荷载~折减系数和极限荷载比例系数~折减系数两种曲线。

图8 极限荷载随折减参数的变化曲线(E×100倍)
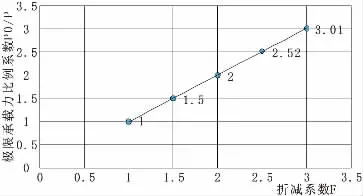
图9 折减参数与极限荷载比例系数的关系曲线(E×100倍)
图8 和图9满足随着折减系数的增大,极限荷载在减小和变化曲线可得极限承载力比例系数与折减系数之间基本上呈斜率为1的直线的验证条件。
6 算例应用
陕西某铝镁合金项目配套电力设施,工程场地长约884 m,宽约450 m,工程主厂房采用现浇钢筋混凝土框架结构,要求基底压力≥400 kPa,地基为黄土,相关土体物理指标及荷载板参数见表3。
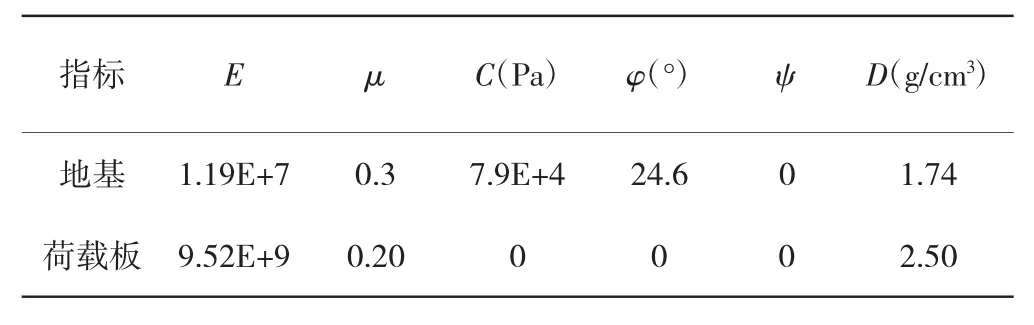
表3 相关物理指标

图10 地层关系图

图11 地基模型和边界条件
建立如图11所示计算区域为尺寸为50 m×50 m×20 m规则结构,包含土体结构和混凝土承载板,承载板面积为5000 m2,厚度为1 m,计算边界四周采用法向约束,底部采用全方向约束的计算模型。
在保持外荷载400 kPa不变时,通过等比例折减强度参数粘聚力和材料参数容重,当土体达到极限状态时,得到的折减系数即为土体极限承载安全系数,进而可以得到土体的极限承载力。

图12 塑性区贯通时等效塑性应变云图
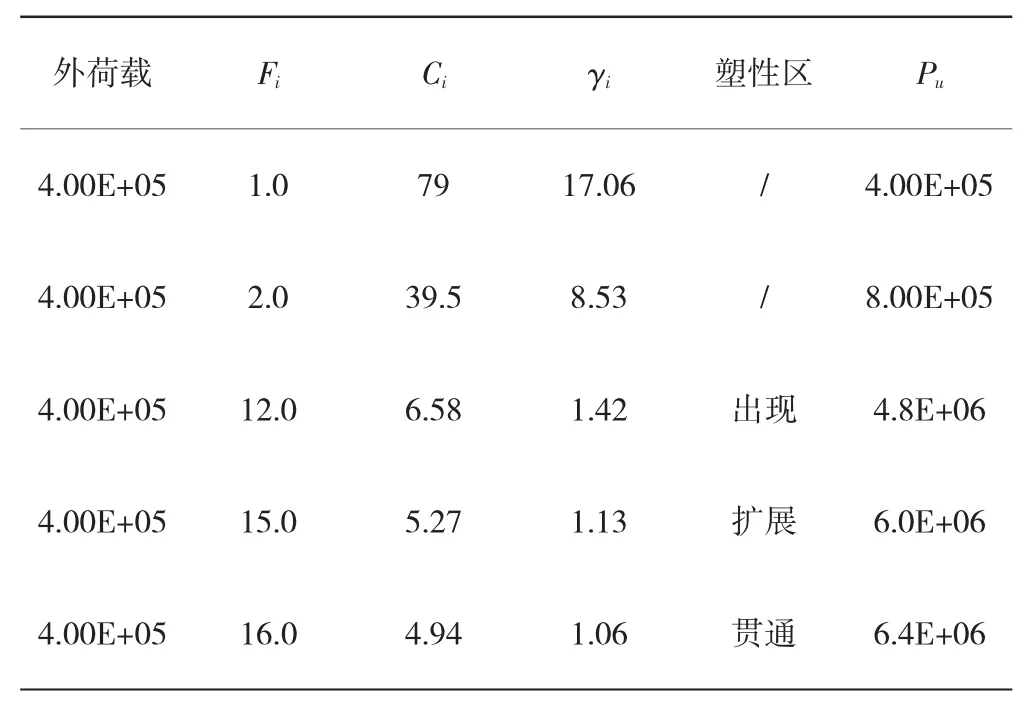
表4 计算结果汇总表
按照表4计算结果所示,当F=16.0 Pa时,相应的极限承载力为Pu=P·Fs=6.40E+6Pa,结果相对于由原位平板静力载荷试验得到的承载力特征值3.75E+6Pa值偏大,主要是由于对计算模型进行了简化和前提假设、计算精度及参数不够精确引起的。
7 结论
本文通过借鉴有限元强度折减法理论,创新式的调整折减参数后应用与地基极限承载力计算和稳定性分析中,得到以下结论:
(1)参数折减法基于太沙基地基承载力公式,通过数学推导,存在参数和的线性数学关系,理论支撑明确,可以借助有限元数值方法进行计算。
(2)利用极限承载力比例系数与折减系数的线性关系、极限承载力随折减系数的变化规律可以验证数值计算结果的正确性。
(3)通过单一调整承载板尺寸和地基物理指标进行折减计算结果分析,参数折减法仍然适用。
(4)对某一实际工程算例进行数值计算发现,计算结果与实际荷载试验相比偏大,由于数值计算的模型简化和计算假定引起的。
——结构相互作用的影响分析

