关于排列组合问题的一些教学体会

陈 浩

(陕西省咸阳市西藏民族大学附属中学 712082)

新课改中，提倡教师对教学情景的创设，注重对生活情趣的创设．那么如何将学生感觉学习起来比较困难的排列组合问题，转变得与实际生活联系紧密，让有些问题更像游戏规则，致使学生对这一部分有更高的兴趣呢？下面就排列组合中的一些经典问题，谈谈自己在教学中的体会和做法．

一、关于“谁选谁”的问题

例1 4名同学分别报名参加学校的足球队、篮球队、乒乓球队，每人限报其中的1个运动队，不同报名方法的种数是34还是43？(人教版新课标高中数学A版选修2-3第15页B组第2题的1小题)

解析由分步计数原理可知，完成这件事，分了4步，即每名同学选报一个队有3种方法，所以N=3×3×3×3=34.

但是，在教学中发现学生对解题过程的理解有较大困难．我通过寻找教学与学生生活的结合点，成功地使学生明白了此类问题的解题思想．

二、关于排列组合中的分组问题

分组问题是排列组合教学中的一个重点和难点，学生不易理解． 针对藏族学生的学情，我们要将学生熟悉的生活情景融入数学教学，去探索一条适合藏族学生的数学教学方法．于是，我通过将此类问题变形为将书以不同的形式分给班上的学生．学生看到自己的名字出现在黑板上的问题中，自然而然就提高了他们的学习兴趣，从而调动了学生的学习兴趣．接着，趁热打铁，引导学生进行归纳总结解决此类问题的方法与规律：一方面，审题要清，搞清楚是哪类分组问题，对症下药；另一方面，利用好加法原理和乘法原理这两个解排列组合应用题的最基本的出发点．

1．非平均分组问题

(1)非平均分组，没有分配对象

例2 6本不同的书分为三组，一组3本，一组2本，一组1本，有多少种分法？

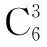
(2)非平均分组，有确定分配对象(非平均定向分配)

例3 6本不同的书分给3人，曲增3本，普参2本，次曲1本，有多少种分法？

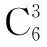
(3)非平均分组，分配对象不固定(非平均分组不定向分配)

例4 6本不同的书分给巴珠、央金卓玛、旦增曲吉3人，1人3本，1人2本，1人1本，有多少种分法？

2．平均分组问题

(1)平均分组，没有分配对象

例5 6本不同的书平均分成3组，有多少种不同的分法？

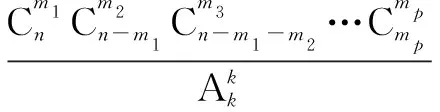
(2)平均分组，分配对象不固定(平均分组不定向分配)

例6 6本不同的书平均分给索珍、尼珍、普参3人，有多少种不同的分法？

解析由于学生有前面非平均分组不定向分配问题的经验，很快就总结出平均分组不定向分配问题的解法，即先平均分组，再分配，与顺序有关，需排序．利用分布计数原理可得：第一步先平均分组有

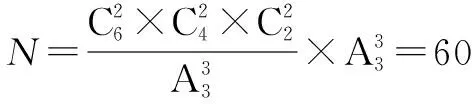
(3)部分平均分组，没有分配对象

例7 6本不同的书分成4组，一组3本，其余各组各1本，有多少种不同的分法？

解析学生利用结合2．1．1和2．2．2的解题方法，总结出部分平均分组，没有分配对象问题的解法，即仅仅分组, 分组与顺序无关，是组合问题．利用分步计数原理得

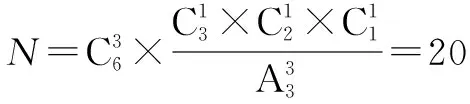
(4)部分平均分组，不定向分配

例8 6本不同的书分给欧青、旺旦、次德吉、德庆4名同学，每人至多2本，有多少种不同的分法？

解析首先要搞清楚“每人至多2本”是什么意思，即分配本数为“2、2、1、1”，然后引导学生结合2．1．3和2．2．3的解题方法，总结部分平均分组，不定向分配问题的解法，即先部分平均分组，再分配，与顺序有关，需排序．利用分步计数原理可得：第一步先部分平均分组有

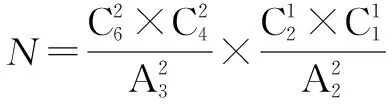
通过在教学情境中创设生活环境，激发了学生的学习积极性，帮助学生顺利理解和掌握了分组问题，类别归纳了分组问题解题思路，提高了学生的分析能力、归纳能力．而且，学会了分组问题，还能将一些其他的排列组合问题转化为分组问题来解决．