基于改进粒子群算法的物流车辆路径优化问题研究

孟宪秋 邱春艳 姜建华 刘洋 吉林财经大学管理科学与信息工程学院

引言：车辆路径问题（Vehicle Routing Problem，VRP）来源于交通运输，由Dantzing和Ramser在1959年首次提出的运输组织优化中的核心问题，也是运筹学的一类经典组合优化问题。智能优化算法是一种基于物理或仿生学原理的元启发式算法，如模拟退火算法，禁忌搜索算法，遗传算法，粒子群优化算法等，智能优化算法能够在有限的时间内求解车辆最优路径，成为求解车辆路径问题的常用算法。由于粒子群在求解车辆路径问题时性能良好，因此该方面的研究逐渐得到学术界的广泛重视。

国内学者在解决车辆路径问题时主要采用两类策略：一类是使用非智能算法进行求解车辆路径问题，此方法可以有效的结解决车辆路径问题；另一类是智能算法进行求解车辆路径问题，包括单目标算法，改进的单目标算法以及混合的智能算法。本文采用粒子群优化(Particle Swarm Optimizer,PSO)算法，将惯性因子设为0，可以增加收敛性且增强局部搜索能力，因此较为客观。

1 基本问题描述及模型建立

1.1 问题描述

车辆路径优化也就是旅行商问题，即对每辆车所走的路径进行优化，以达到整体路径最短。

问题描述：一个中心仓库序号为0，7个仓库序号为1-7，其位置坐标见表1，中心仓库有3辆车，容量均为1，由这3辆车向7个需求点进行货物配送，出发点和收车点都是中心仓库，求解物流配送车辆的最优路径。

1.2 模型构建

本论文引用[5]中的模型，问题简述为：有L个仓库（以1,2.....L表示），拥有K辆车（k表示第k辆车），容量分别为。

模型建立如下：

其中：

2 求解物流车辆路径的粒子群智能算法

2.1 粒子群算法数学描述及局限

粒子群算法是通过模拟鸟群捕食行为提出的一种智能算法。PSO算法的工作原理：首先，初始化一组随机解，通过迭代跟踪两个极值完成自我更新，包括局部极值点（用pid表示其位置）和全局极值点（用pgd表示其位置）；然后在每轮迭代中，粒子通过：

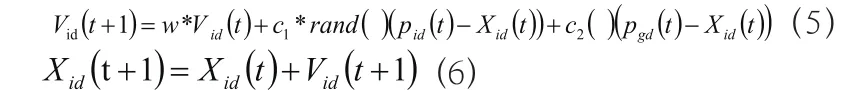
PSO算法的优点是收敛速度较快，算法简单，容易编程实现。算法的缺点在于对于有多个局部极值点的函数，容易陷入到局部极值点；算法虽然提供了全局模索的可能，但是不能保证收敛到全局最优点上。

2.2 改进的粒子群优化算法

本文在原有粒子群算法的优点基础上进行改进，保证粒子群算法的收敛性，即收敛到全局最优点上，并且防止全局最优解陷入全局的极值点。

当惯性系数为0时，公式（5）与公式（6）合并后为：

根据公式可得只有粒子的位移发生变化，简化了粒子进程，仍然保持着收敛性，并且为线性收敛。本文改进的粒子群算法主要步骤如下：

（1）初始化粒子速度和位置，并设置惯性因子为0；

（2）计算粒子的适应度值；

（3）计算个体历史最优解；

（4）计算全局最优解；

（5）根据迭代公式更新粒子的位置和速度；

（6）判断是否带到最大迭代次数，若没有则转到（2）；

（7）算法结束，输出最优解。

2.2.1 初始化

PSO初始化为一群随机粒子（随机解），然后通过迭代寻求最优解，在每次叠代过程中，粒子通过跟踪两个"极值"来更新自己的速度和位置。

当W=0，第一个解是个体极值（即第一次的解是粒子本身所找到的最优解）；第二个极值是全局极值（即整个种群目前找到的最优解）。

粒子群算法的初始化过程如下：

（1）设定群体规模n；

（2）对任意i,j在内服从均匀分布产生；

其中：i，j分别为：“j”表示粒子的第j维，“i”表示第i个粒子；分别表示第i个粒子的最佳位置与当前位置。

3 实验结果与比较

3.1 样本集描述及参数设置

根据文献[4、5]中的问题设置初始值，中心仓库用0表示，设每辆车运货量q= 1.0，共3辆车完成任务。

（1）初始化粒子群为n=40，惯性因子w=0，学习因子c1=c2=1.4944，最大代数为100，搜索空间维数（未知数个数）为40，运用上述建立的车辆路径模型以及粒子群算法进行求解。

（2）利用坐标间计算公式得到需求点之间的距离：

3.2 实验过程

当惯性系数为0时，粒子的飞行速度只取决于粒子的当前位置，历史最好位置和粒子群的历史最好位置，对于全局最好的粒子将保持不动，其他粒子则倾向与最好位置的粒子进行移动，即粒子群将收缩到全局最好的位置。根据代码执行的结果可知，当迭代到第12次得到最优值，最优的行车总距离为217.8135。

图1 最终非劣解在目标空间的分布

根据图1可以得出，改进后非劣解的数量减少，整个进化方程具有很强的局部搜索能力，且改进后的粒子群算法收敛性增加，并且不再出现局部极值代替最优值情况。

4 结论

本文主要对粒子群算法进行改进，使粒子群算法避免了在搜索最优值时出现局部极值代替全局最优值和难以找到最优解的情况，提高了微粒群算法的收敛性，达到最优值时迭代次数变小，缩减了时间。