洞态Ar原子Kα和Kβ伴线和超伴线的理论计算∗

马堃 焦铮 蒋峰建 叶剑锋 吕海江 陈展斌

1)(黄山学院信息工程学院,黄山 245041)2)(湖南工业大学理学院,株洲 412007)3)(国防科学技术大学理学院,长沙 410073)(2018年3月28日收到;2018年5月28日收到修改稿)

1 引 言

洞态原子是指内壳层电子被激发或电离后形成的激发态中性原子或近中性离子.它广泛存在于实验室和天体等离子体中,尤其是在高能炮弹离子或者同步辐射光源与原子碰撞的反应产物中.洞态原子也是等离子体物理学、天体物理学和固体表面物理学的研究对象之一.由于旁观空穴的存在,导致洞态原子核外电子对原子核的屏蔽效应减弱,从而使得辐射跃迁线的能量略高于主线能量,即伴线.当内壳层有两个空穴存在时,屏蔽效应进一步减弱,外壳层电子向该壳层跃迁时辐射跃迁线的能量更高,即超伴线[1].通过对空心原子退激辐射产生的X射线伴线和超伴线结构的研究,不仅可以揭示洞态原子的形成机制,而且为等离子体状态诊断、新的极紫外和X射线光源的发展提供重要的理论支持.对于K-X射线,由于K壳层电子被紧密地束缚在原子核周围做高速运动,电子间的Breit效应、量子电动(QED)等高阶相对论效应十分显著.因此,有必要在全相对论理论框架下对K壳层辐射X射线进行理论计算.Kozioł等[2]利用多组态Dirac-Fock理论(MCDF)方法计算了Al和Si原子Kα1,2X射线结构和宽度,讨论了电子关联效应和伴线结构对辐射X射线谱结构的影响;2015年,Wang等[3]在相对论框架下计算了洞态原子(Z=13—90)退激辐射Kα,β,γX射线伴线结构,并分析了旁观空穴对其谱线结构的影响,结果表明相对论计算结果与实验测量谱具有很好的一致性.

在早期的实验室中,人们主要利用光子或电子与靶原子碰撞产生洞态原子,洞态原子通过退激辐射产生伴线和超伴线.超伴线的产生条件比伴线苛刻,要求洞态原子在辐射跃迁时有两个空穴位于初态的同一壳层上.一般而言,需要两步过程才能实现这样的洞态原子,如第一步先电离掉一个电子,第二步再通过伴随振离或者Coster-Kronig(CK)跃迁产生第二个洞态.然而这些过程的跃迁强度都非常弱,实验上也不易探测.在重离子碰撞过程中,由于其提供的强库仑场,碰撞时可以同时将多个电子电离,并产生丰富的退激X射线主线、伴线和超伴线.近年来,随着重离子储存环和加速器等实验技术的进步,人们越来越关注高能离子与原子碰撞产生洞态原子过程,尤其对洞态原子退激产生的X射线伴线和超伴线谱的研究更加感兴趣[4,5].2013年,Czarnota等[6]利用高分辨率的晶体谱仪对280 MeV能量下O6+离子与Zr,Mo和Pd原子的碰撞过程进行了研究,通过对退激Lα12(L3→M4,5)和Lβ1(L2→M4)X射线伴线和超伴线光谱的计算模拟,得到了重离子碰撞过程中靶原子空穴产生概率.最近,中国科学院兰州近代物理研究所基于HIRFL大科学装置[7],开展了一系列高能离子碰撞的实验研究,特别是在高能裸核Xe炮弹离子与Kr和Xe靶原子碰撞过程的实验研究中,观察到了明显的伴线和超伴线结构[8].为了对这些复杂的X射线谱进行指认,并进一步分析高能碰撞过程中各种洞态产生的物理机制,董晨钟等[9−11]基于MCDF方法,对高能裸核Xe离子与Kr原子和Xe原子碰撞的辐射复合过程以及退激辐射产生的K-X射线伴线和超伴线结构进行了理论计算,指出了辐射复合是洞态产生的主要机制.本文利用MCDF理论方法,对L壳层旁观空穴下,Ar原子退激辐射X射线的能量和强度进行了系统的理论计算;分析了L壳层旁观空穴对退激辐射X射线能量的影响,给出了L壳层旁观空穴个数与伴线和超伴线能移之间的关系.相关计算结果可以为重离子碰撞实验研究提供理论支持.

2 理论方法

有关MCDF理论方法及GRASP2K程序包,文献[12,13]已做了详细的描述,这里仅做扼要的介绍.在MCDF理论方法中,N电子体系的Dirac-Coulomb哈密顿量可以表示为

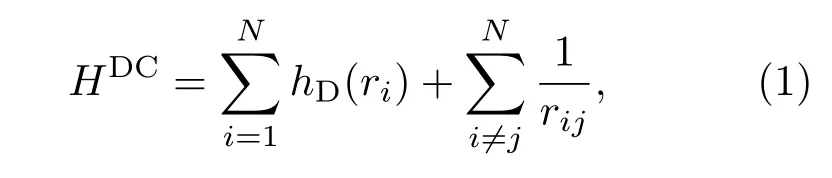
其中hD(ri)是单电子Dirac哈密顿量,包括单电子动能项和电子与原子核之间相互作用能项,具体可以写成

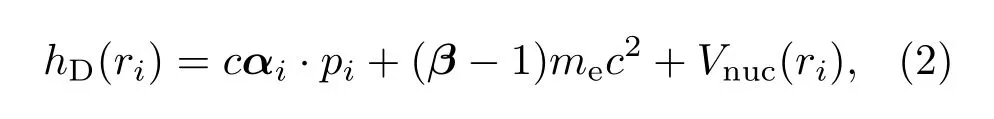
(2)式中,c表示真空中的光速,α和β表示Dirac矩阵,pi是电子动量.(1)式中的第二项表示电子与电子之间的相互作用势.

在MCDF计算中,原子态波函数|α(PJM)〉可以采用具有相同总角动量J和宇称P的组态波函数|γrPJM〉线性组合得到,即

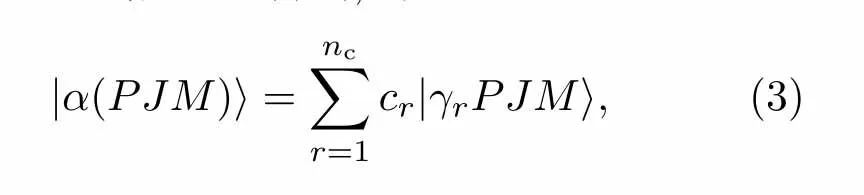
其中nr表示原子态波函数展开时采用的组态波函数基矢个数,cr为组态混合系数,γr表示确定组态信息的其他量子数.组态波函数|γrPJM〉由一组正交轨道反对称化乘积得到,相应的系数通过对Dirac-Coulomb哈密顿优化得到.

对于中Z和高Z元素,尤其是对空心原子,除了Dirac-Coulomb哈密顿外,由磁效应和弛豫效应引起的Breit相互作用以及QED效应较为显著.Breit相互作用算符可以表示为

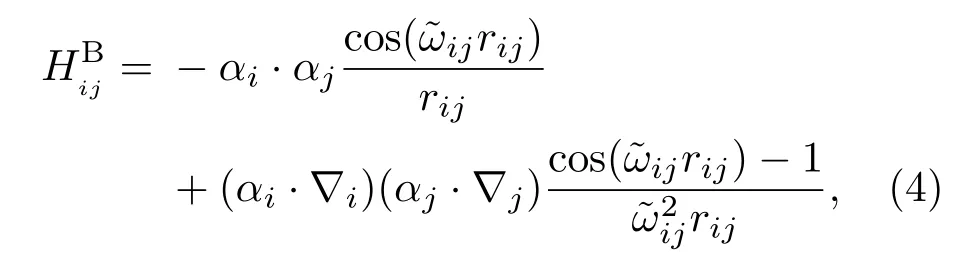
式中˜ωij表示相互作用过程中虚光子交换频率.本文在具体计算时,还包括了自能、真空极化等QED效应中的主要修正项[12].

按照Fermi黄金定则,单位时间内从辐射初态到辐射末态的跃迁概率可以表示为

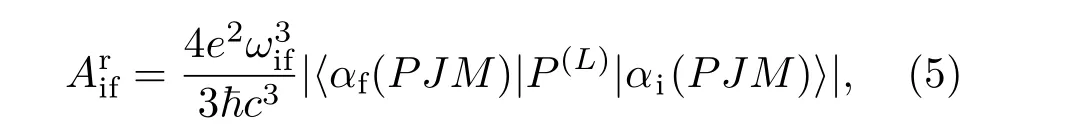
其中|αi(PJM)〉和|αf(PJM)〉分别表示初态和末态原子态波函数,P(L)是辐射电磁场的L阶张量算符,本文仅考虑电偶极辐射跃迁,即L=1,ωij是初态和末态跃迁频率.

需要指出的是,在具体计算时,跃迁概率有Coulomb和Babushkin两种规范,分别对应非相对论极限下的速度规范和长度规范.这两种规范下计算结果的一致性可以作为计算准确性的评判条件之一.本文分别计算了Coulomb规范和Babushkin规范两种规范下的结果,发现卷积之后的辐射谱形状以及能量位置没有明显差别.因此,文中只给出Coulomb规范下的结果.

3 结果与讨论

洞态原子退激辐射X射线谱结构不仅与内壳层空穴的产生机制有关,而且与其退激发辐射动力学过程有关.由于本文研究辐射跃迁涉及到K壳层,因此在MCDF理论框架下进行计算更加合适,计算中包括了Breit作用和QED修正等.表1给出了不同初始组态下的跃迁谱线条数.其中组态K−kL−l表示K壳层有k个洞,L壳层有l个洞,其他外壳层电子满壳层排布.具体地,如K−1L−2表示K壳层有1个空穴,L壳层有2个空穴,其他外壳层电子满壳层排布.相应的跃迁线可以用1s−1L−2→np−1L−2表示,其中n=2和3分别表示L壳层有两个旁观空穴下的Kα(1s→2p)和Kβ(1s→3p)X射线伴线.该组态在MCDF计算中,共产生317条跃迁线.需要指出的是,本文仅考虑初态为K−kL−l(k=1,2;l=0—8)的情况,没有涉及M壳层空穴情况.事实上,M壳层每增加一个空穴,跃迁线条数将增加很多.以Ar原子为例,初态为K−1L−2M0组态跃迁线有317条,若M壳增加一个空穴,即 K−1L−2M−1组态,其跃迁线达到16539条.从文献[9]计算结果可以看出,M壳层对跃迁的影响很小,可以忽略.因此,本文没有对M壳层空穴情况进行研究.

利用MCDF方法,计算了表1中列出的所有跃迁线的跃迁能量和跃迁概率.具体地,靶态的初、末态波函数和能级的计算采用GRASP2K程序包,计算中包括了Breit作用和真空极化、自能等QED修正,采用了扩展优化能级方案(EOL).跃迁概率采用RATIP程序包中REOS模块[14]计算,该计算方案分别导入GRASP2K程序计算的初态和末态波函数,可以充分考虑跃迁前后电子轨道的弛豫效应.表2列出了Kα1,2(1s→2p3/2,2p1/2)和Kβ1,3(1s→3p3/2,3p1/2)主线的跃迁能量和跃迁概率.作为比较,表中同时列出了文献[15]中的跃迁能和跃迁强度数值,其中跃迁强度归一到Kα1谱线.表中“NR”列的数据表示非相对论计算的跃迁能,“R”列数据表示包括了Breit和QED效应之后的跃迁能.从表中可以看出,本文计算的跃迁能量和跃迁概率与文献[15]结果符合得很好,如能级的最大误差仅为0.02%.Kα1,Kα2之间的能量差和Kβ1,Kβ3之间的能量差分别为2.16 eV和0.18 eV.Kα1/Kα2和Kβ1/Kβ3跃迁概率之比分别为1.9777和1.9785,这与1s→2p3/2和1s→2p1/2跃迁初态统计权重(2J+1)之比一致.

表1 在MCDF计算模型下主线、伴线和超伴线X射线跃迁数目Table 1.Number of transitions calculated within the MCDF model for various diagram,satellites and hypersatellites X-ray lines.

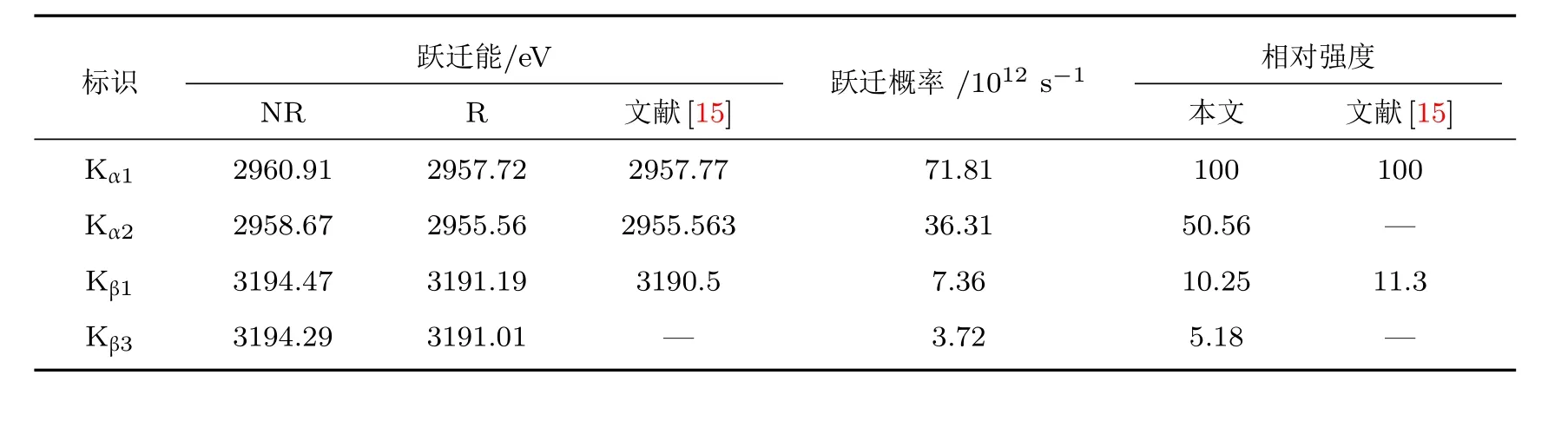
表2 Ar原子主线的跃迁能量、跃迁概率和相对强度Table 2.The transition energies,rates and relative intensity of diagram lines for argon atom.

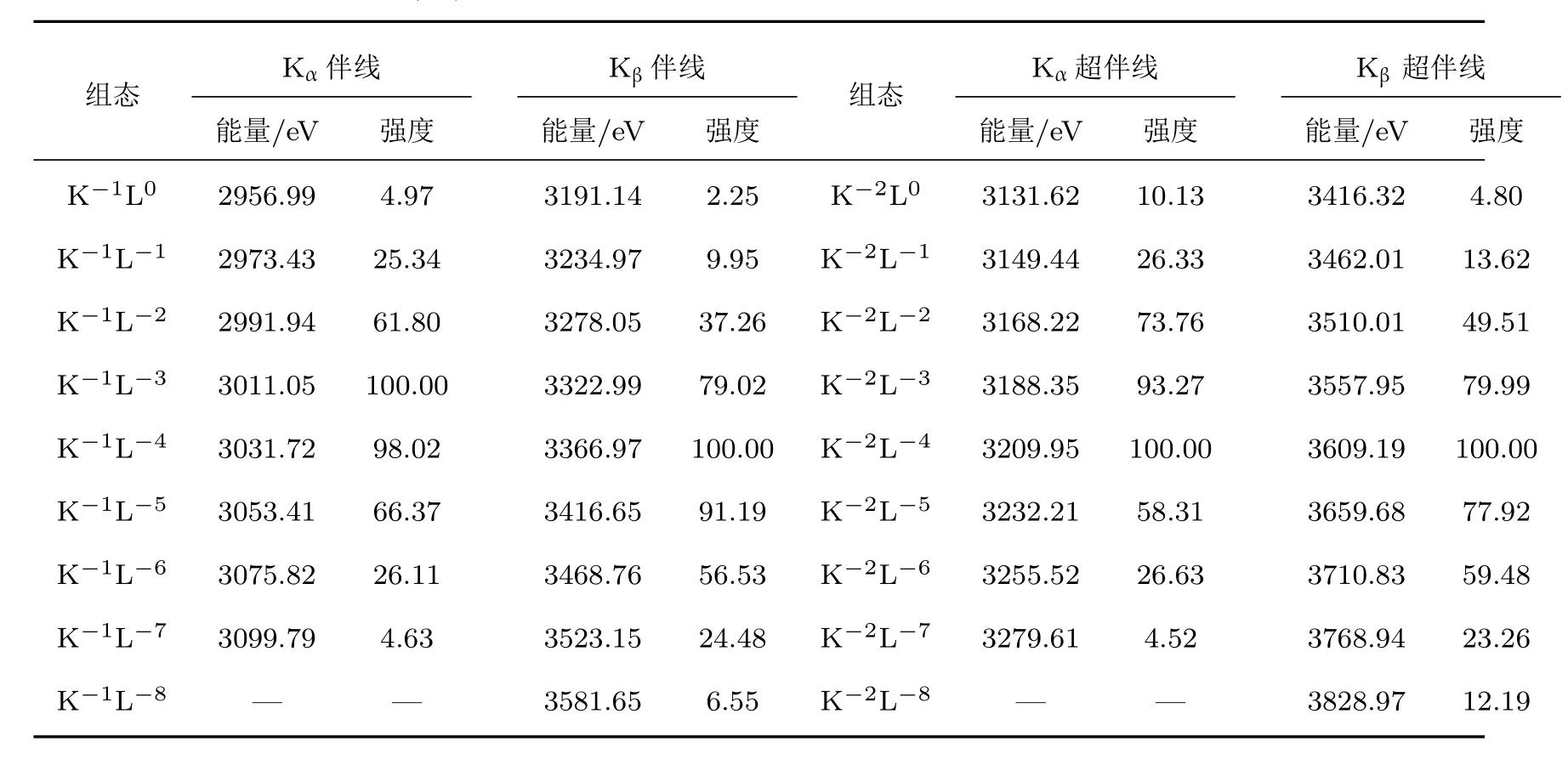
表3 Ar原子K X射线伴线和超伴线平均跃迁能量和相对强度Table 3.Average energy(eV)and relative intensity of K X-ray satellite and hypersatellite lines for Ar.

在原子跃迁过程中,由于各种谱线加宽机制导致每条跃迁谱线都不是严格的分立谱,而是具有一定的宽度.考虑到实验装置测量的分辨率,我们采用20 eV的半高全宽(FWHM),将表1中所列出的18个初始组态(K−kL−l)对应的所有跃迁线的跃迁能量和跃迁概率按照高斯线型展宽,从而得到L壳层旁观空穴下洞态Ar原子退激发辐射X射线谱的分布情况,结果在图1中给出.展宽时,近似地对每个初始组态所涉及的多条跃迁谱线按照等权重方案进行叠加.其中,图1(a)给出了L壳层不同空穴数下的辐射谱线,从展宽得到的谱线轮廓中可以确定各谱线峰值的位置和高度,即对应该组态的平均跃迁能量和强度,结果列于表3.在表3中将每一列跃迁强度归一到其最强谱线,如Kα伴线跃迁强度归一到K−1L−3组态跃迁强度,Kα超伴线跃迁强度归一到K−1L−4组态跃迁强度,Kβ伴线和超伴线跃迁强度均归一到K−2L−4组态的跃迁强度.从图1(a)可以看出,超伴线位于伴线右侧,即超伴线跃迁能量大于伴线的跃迁能量.这是由于超伴线比伴线多一个K壳层旁观空穴导致的.另外可以看到,L壳层的旁观空穴也会改变Kα和Kβ伴线和超伴线的跃迁能和跃迁强度.随着L壳层旁观空穴数的增加,Kα和Kβ伴线的强度先增加后减少.L壳有3个旁观空穴时Kα伴线最强,L壳有4个洞时Kα超伴线、Kβ伴线和超伴线最强.这是由于跃迁线的条数随着L壳层空穴数的增加先增加再减小导致的.随着L壳层空穴数的增加,辐射线的能量逐渐向高能端偏移,导致Kα的超伴线与Kβ伴线.图1(b)是将图1(a)中18个初组态(K−kL−lk=0,1;l=0—8)退激辐射跃迁谱线按照等权重叠加后得到的合成光谱.从图1(b)中可以看出,Kα的伴线和超伴线可以较好地分辨,但Kβ的伴线和超伴线重叠在一起,同时Kα的超伴线与Kβ的伴线也有部分重叠.本文选取20 eV的展宽主要考虑到实验测量装置的分辨率.如果实验测量的分辨率更高,则可以分辨出更多谱线对应的位置.

图1 Ar原子Kα和Kβ主线、伴线和超伴线理论计算谱(FWHM=20 eV)Fig.1.The calcultaed spectra corresponding to Kα and Kβdiagrams,satellites and hypersatellites of Ar atom(FWHM=20 eV).

为了更加清晰地揭示L壳层旁观空穴对辐射X射线能量的影响,图2给出了跃迁辐射Kα和Kβ的伴线和超伴线能量与L壳层空穴个数之间的关系,其中Ksαβ和Khsαβ分别表示伴线和超伴线.从图2中可以看出,随着L壳层空穴个数的增加,跃迁能也随之增加,并呈现线性关系.同时我们发现,Kα的伴线和超伴线斜率相近,Kβ的伴线和超伴线斜率相近,即L壳层旁观空穴对Kα(Kβ)伴线和超伴线产生的能量移动近似相等.

图2 Ar原子Kα和Kβ伴线和超伴线跃迁能与L壳层空穴个数之间的关系Fig.2.Transition energy of the Kαand Kβstatellite and hypersatellite versus the number of the spector vacancies in the L shell for Ar atom.

图3给出了辐射X射线能移ΔE(K,Ln)=E(K,Ln)−E(K,L0)与L壳层空穴个数的关系.可以看出K-X射线能移大小随着L壳空穴个数的增加而增加,并具有明显的线性关系.L壳层相同空穴数下,超伴线的能移略大于伴线的能移.这种差别主要是由于超伴线比伴线在K壳层多一个旁观空穴,电子的屏蔽效应减弱,参与跃迁的电子感受到原子核的效应更强导致的.基于计算得到的能移与L壳层空穴个数的数据关系,利用最小二乘法给出了能移大小与L壳层空穴个数的拟合关系式,具体表示如下:

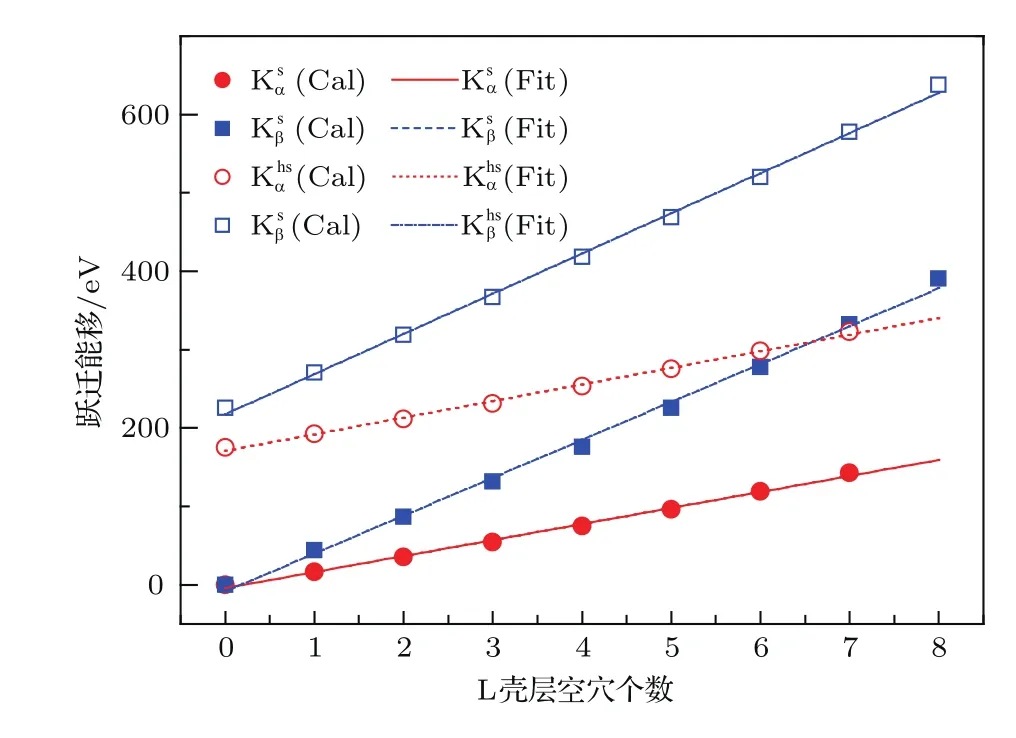
图3 Ar原子Kα和Kβ伴线和超伴线能移与L壳层空穴个数的关系 (Cal表示利用MCDF方法计算的结果;Fit表示拟合公式(6)得到的结果)Fig.3.Energy shifts of the Kαand Kβstatellite and hypersatellitev versus the number of the spector vacancies in the L shell for Ar atom(Cal denotes the data calculated by MCDF method,Fit denotes the data from Eq.(6)).

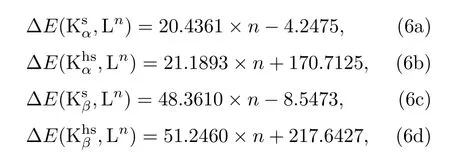
式中n为L壳层旁观空穴个数.图3给出了利用这些拟合公式得到的跃迁能移与L壳层空穴个数之间的关系曲线,可以看出,拟合公式得到的结果与MCDF计算的结果符合得很好.

4 结 论

本文利用MCDF理论方法计算了Ar原子K−kL−l→K−k+1L−l−1(k=1,2;l=0—8)Kα和Kβ主线、伴线和超伴线的跃迁能和跃迁概率,计算中包括了Breit相互作用和QED修正.计算结果与文献中已有的数据符合得很好.以跃迁能为例,本文计算的结果与文献中的数据误差均小于0.02%.采用20 eV半高全宽对每个组态下所有可能的辐射跃迁线进行了高斯展宽,得到其高斯线型,进而确定出不同组态分别对应的平均跃迁能量和跃迁强度.分析表明,L壳层旁观空穴会导致辐射跃迁线向高能端偏移,其能移的大小与L壳层空穴个数呈线性关系.利用最小二乘法拟合出了能移与L壳空穴数之间的线性表达式.本文的研究结论为定量地解释原子碰撞过程中产生X射线谱提供了必要的理论支持.需要说明的是,对于洞态Ar原子,除了辐射X射线退激途径外,还存在Auger过程,本文并没有对非辐射的Auger退激途径进行研究,相关工作将在后续进一步报道.

感谢中国科学院近代物理研究所邵曹杰博士对本文研究给予的帮助.