诱导空间非相干束匀滑技术的近区特性及改善技术∗

李福建 高妍琦 赵晓 季来林 王伟 黄秀光马伟新 隋展 裴文兵

1)(中国工程物理研究院上海激光等离子体研究所,上海 201800)2)(中国科学院上海光学精密机械研究所,高功率激光物理联合实验室,上海 201800)3)(上海交通大学,IFSA协同创新中心,上海 200240)(2018年3月26日收到;2018年5月23日收到修改稿)

1 引 言

聚变能是解决人类未来能源问题的重要途径之一,实现可控聚变主要有两种方案:惯性约束聚变与磁约束聚变,目前两者都面临着严峻的技术挑战[1,2].在激光驱动惯性约束核聚变实验中,需要通过聚焦激光得到极高的能量密度.为了控制激光与等离子体相互作用,又需要得到均匀性好的激光辐照场[2].在具体的高功率激光装置中,如果不采取束匀滑措施,因为光路中的相位畸变,焦斑形态将会很不规则,激光辐照的均匀性将难以控制.诱导空间非相干技术(induced spatial incoherence,ISI)是Lehmberg和Obenschain[3]于1983 年提出的一种束匀滑方法[4,5],使用在KrF激光器上,得到了均匀性极好的焦斑[6].但是使用ISI技术得到的光束在光路中存在时空上的强度跳变,这种强度跳变一方面严重影响了装置的运行安全,另一方面影响了装置的放大输出能力[7].ISI可以分为两种:第一种使用低时间相干性的宽带光源,通过两个阶梯状的反射镜将光束分割为有时间差的、互相不相干的子光束;第二种使用放大的自发辐射(ampli fied spontaneous emission,ASE),通过在前端增加小孔来改变靶面的光场分布,理论上,靶面的光场形态与小孔的形态相同.尽管第二种ISI系统简单,但是多模ASE光束在传播中会出现光强和近区强度分布的快速随机变化[8,9],低时间相干性和低空间相干性的近区耦合重叠作用使得输出光束的时间品质和空间强度分布品质较难保证.而第一种ISI所得到的光束将近区和远区特性分离,其平稳性好于第二种ISI.理论分析表明,同时使用阶梯状反射镜式ISI与连续相位板(continuous phase plates,CPP)[10−12]可以使焦斑达到极好的匀滑效果.其中ISI可以理解为时间匀滑装置,CPP可以理解为空间整型装置.相比于其他束匀滑技术[13−15],ISI+CPP束匀滑技术具有自身独特的优势.在空间尺度上,ISI+CPP可以通过合适的CPP设计来获得完全平整的焦斑与完美的轮廓.在时间尺度上,ISI+CPP匀滑得到的焦斑的散斑分布则会随着时间快速跳变,每过一个相干时间,焦斑的散斑分布就会发生重构.这种重构,一方面消除了强度分布的时间积分中的散斑,另一方面,快速的强度跳变,类似于延迟尖峰脉冲序列匀滑方式(spike trains of uneven duration and delay,STUD),能进一步抑制激光与等离子体相互作用过程中的不稳定性的发展[16,17].但ISI方法也有其劣势,其中之一就是ISI处理导致的严重近区调制.经过ISI处理后的光束在传播过程中,因为子光束宽度很小,光传播的衍射效应更加明显,这将引起强度的空间调制,对激光的传输放大过程极为有害.为了消除这种强度空间调制,可以在前级增加一个双透镜滤波系统.本文通过理论分析与计算模拟,对双透镜滤波系统对诱导空间非相干结合连续相位板的束匀滑方式导致的近区调制的抑制效果进行了深入、系统的分析与评估.

2 原 理

2.1 ISI+CPP匀滑方法

在高功率激光系统中,焦斑的不均匀性源于光的干涉.因为系统中的误差以及放大光路引入的波前畸变导致在焦平面处不同光程差的子束发生干涉,导致最终焦斑形态不是理想的夫琅禾费衍射,甚至是不规则的.如果能够减少光的干涉现象,就能得到匀滑的焦斑.在ISI中,通过两个互相垂直放置的、侧视图如图1形态的反射镜,将光束分割为一个个子光束.其中第二个反射镜的阶梯高度应该是第一个反射镜的总高度.本文中称ISI将光束分割的子束个数为ISI分割数,例如8×8分割的ISI中,子光束共有64束,8×8代表横纵方向上各分割出8个子光束.

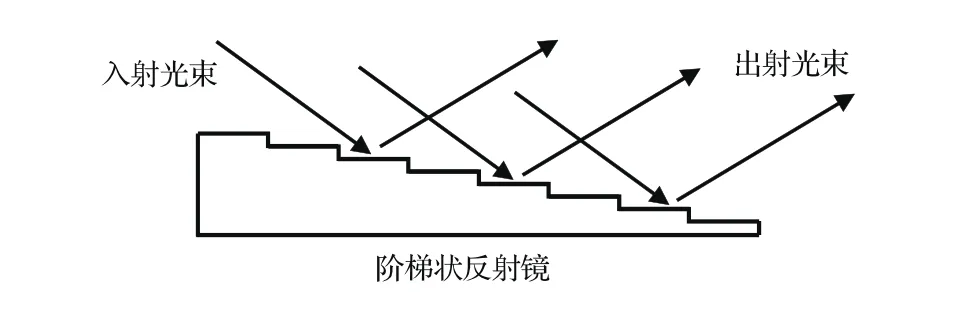
图1 阶梯状反射镜引入时间延迟示意图Fig.1.Schematic of stair-like echelon inducing time delay.

使用ISI方法得到的子光束间都存在时间延迟.如果时间延迟大于光源的相干时间,就可以认为子光束相互不相干,当积分时间足够大时,它们在焦平面强度叠加.如果认为子光束的传播不受波前畸变影响,那么每个子光束在焦平面都会形成一个相同的夫琅禾费衍射像,强度叠加后,形态不发生变化.但这样得到的焦斑形态仍然不是大多数物理实验所追求的“平顶分布”焦斑.控制焦斑形态一般通过使用连续相位板,联用ISI与CPP得到的焦斑的不均匀性随积分时间变化满足方程:

其中σinf是经无穷长匀滑时间最终焦斑强度分布的均方根(root mean square,RMS),σ0=1,是初始强度分布的RMS,σ(T)是经T的匀滑时间得到的焦斑强度分布的RMS,T代表匀滑时间,其单位是相干时间(coherence time,CT).其中σinf可以通过好的CPP设计方法减小到接近0.固定σ0与σinf,系统RMS达到要求所需的匀滑时间与光束的相干时间成正比,增大激光的带宽,便能获得更快的匀滑速度.(1)式不仅仅是ISI+CPP匀滑系统的RMS时间函数,同时对谱色散匀滑也成立[18].

然而使用阶梯状反射镜来分割光束仍然存在问题.经过ISI阶梯状反射镜后,光束分割为不相干的子光束.这些子光束的衍射效应因为光强叠加而得以显现.图2给出了0.4m宽,8×8分割的光束在传播20 m距离后的强度分布,设原光束强度为1.此时强度出现空间调制,最大强度达到了原来的1.8倍以上.

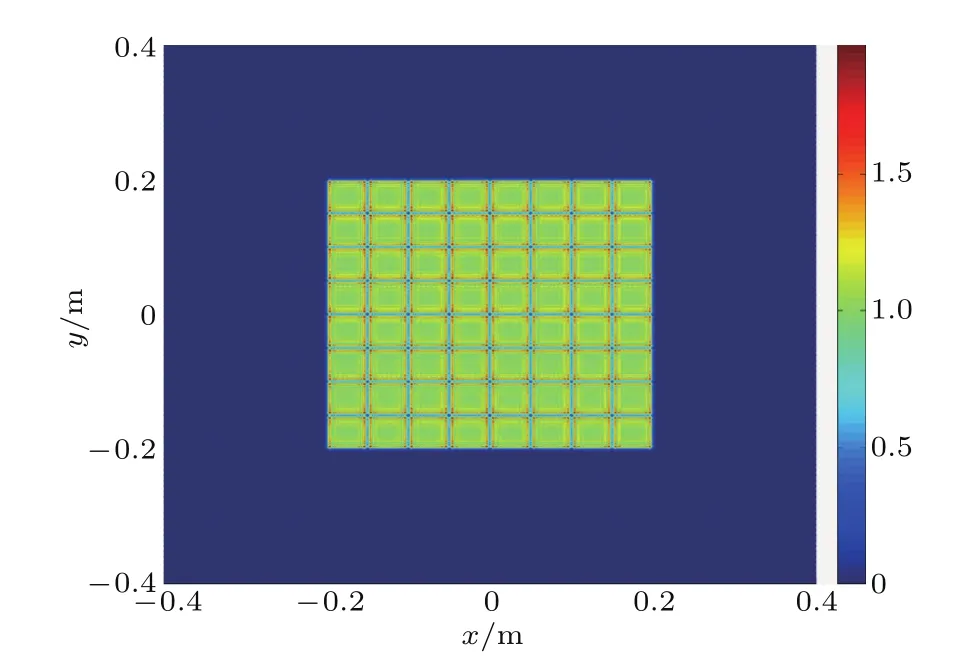
图2 0.4 m宽、8×8分割的光束在传播20 m距离后的强度分布Fig.2.0.4 m width,8×8 ISI division beam intensity distribution after a propagation length of 20 m.

因为强度的空间调制对应着空间频率域的高频成分,所以可以通过双透镜滤波系统抑制强度的空间不均匀性,同时实现扩束.其示意图如图3所示.其中的1是入射的瞬时宽带光;2,3是ISI中引入光程差的阶梯状反射镜;凸透镜4、小孔5和凸透镜6构成一个双透镜滤波系统;用dij表示平面i与平面j的距离(i,j可取为4,5,6,7);f4,f6表示透镜4与6的焦距;用r表示缩放倍数,则有d45=f4,d56=f6=rf4.平面7是平面4的共轭平面.平面8处依次放置倍频晶体、连续相位板、聚焦透镜.使用同上的表示方法,由菲涅耳衍射定律[19],平面7的位置可表示为

因为实际透镜焦距不能太小,一般平面7位置会比较远,为节省空间,放大器将放置于平面7前,这将要求对光束传播衍射效应有严格的控制.

图3 ISI+CPP束匀滑系统示意图Fig.3.Schematic of ISI+CPP beam smoothing system.

2.2 经过双透镜系统的ISI近区强度分布的计算

使用ISI时,不同的小区域的子光束是不相干的,所以近区的强度分布是所有子光束的强度分布的叠加.双透镜系统中,第一个透镜的焦距通过适当选取以在平面5获得合适的衍射极限.对衍射极限,有关系式[19]:

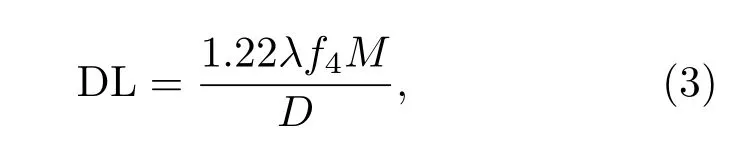
其中DL表示ISI分割后单个子光束在平面5的衍射极限(diffraction limit,DL),M表示ISI分割数,D表示光束总宽度.

单独考虑某子光束,在加入小孔5后,平面7处的电场强度分布可以通过平面4电场强度滤波后按比例放大并旋转得到.考虑到使用对称分布光束,忽略旋转,那么,在平面4的第m行n列的方形子光束经过双透镜滤波系统后在平面7的电场U7mn(x,y)可以通过如下方程计算:

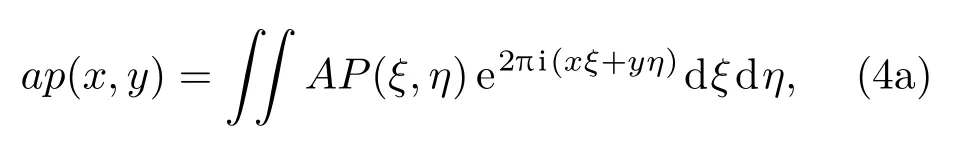
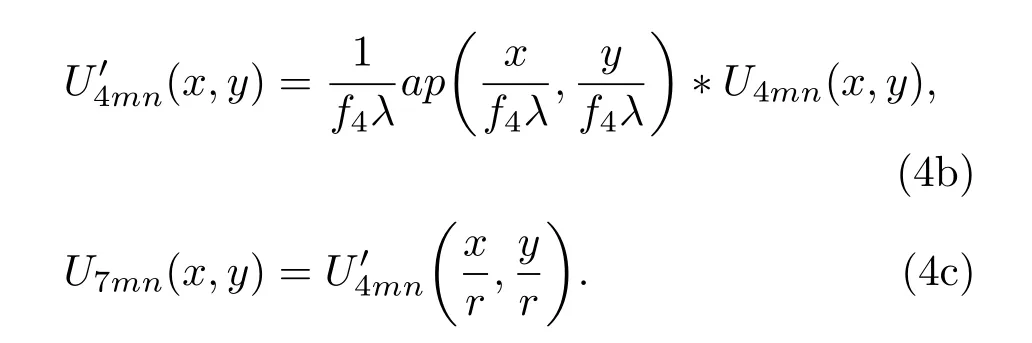
其中U4mn(x,y)表示平面4上第m行n列的方形子光束的电场强度分布;λ表示激光的波长;AP(ξ,η)表示滤波孔的透过率分布;ξ,η,x,y代表相应平面上的横纵坐标;ap(x,y)代表AP(ξ,η)的二维傅里叶变换;是滤波后的结果;*代表卷积. 通过(4)式,给定AP(ξ,η)后,依次求出ap(x,y)与而后便能得到平面7处的场分布U7mn(x,y).

因为ISI光束间强度叠加,用I7(x,y)代表平面7处的总光强分布,则有

进一步利用角谱方法可以计算出与平面7距离为z的平面上的总光强分布:

其中I(x,y,z)表示坐标为x,y,z的点的光强;hz(x,y)表示光场自由空间传播距离z的脉冲响应函数.在计算机模拟中,可以使用角谱法计算,与单步菲涅耳衍射法不同,此方法能够改变计算所得区域的大小[20].

高功率激光系统为了实现最大的输出能力和保障装置的运行安全,其近区强度分布要求具有尽可能好的均匀性和尽可能高的边缘陡峭性.同时,为了保障装置的最大输出能力和提升放大链的能量利用率,要求所有技术单元具有尽可能高的透过率.本文中引用以下3个评价参数作为滤波方法设计优化的评价依据:

A为调制度,定义为光束中心区域最大值与平均值的比值.其中中心区域定义为原光束区域中心的方形区域,其边缘强度是平均值的0.9倍.

B为软化因子,即过度区域宽度/总宽度,过度区域宽度定义为从0.1倍平均光强上升到0.9倍平均光强的宽度,总宽度由0.1倍平均光强的位置决定.

C为透过率,是近区滤波前后光束范围内包含的能量的比值的倒数.

在计算这些参数时,不需考虑扩束过程.当滤波小孔尺寸很小时,单个子光束形态是很宽的高斯型光束,光强叠加后,总光束的光强也接近高斯型.而滤波孔尺寸大时,将出现衍射引起的如图2的强度空间调制.为了得到平均的总光强分布同时减小能量损失,通过计算机模拟选取合适的小孔尺寸与形状.

3 ISI滤波系统设计

设计光束原宽度为0.04 m,经过双透镜系统扩束为0.4 m,假定入射场为理想方形光束,通过ISI引入光程差后分为不相干的小方形光束.

考虑使用3种小孔进行滤波:方形、圆形和高斯型小孔(软边小孔).其中高斯型小孔振幅透过率分布为exp(−ρ2/w2),ρ为半径,w为常数.ISI分割后的子光束将在不同时刻抵达靶平面,这将影响到光束的波形.为了减小对光束脉冲波形的影响,ISI分割数不能过大.假设倍频后获得10 nm带宽,527 nm的2倍频瞬时宽带光[21],其相干时间为93 fs.如果使用32×32的ISI分割,将至少引入0.095 ns的时间延迟,这将增加需要的匀滑时间,并引起脉冲前后沿畸变.为了得到小于100 ps的脉冲前后沿畸变,ISI分割数最好选为16×16或更小.

3.1 传播距离对近区光强分布的影响

ISI分割数越大,引入光程差后的子光束宽度越小,其衍射效应越明显.理想滤波效果应使光束强度分布在放大光路中几乎没有变化.图4给出了使用高斯型软边小孔,ISI分割数为16×16时不同滤波孔尺寸下光束调制度随传播距离的变化.可以看到当小孔尺寸(w)小于0.6 DL时,在200 m范围内调制度几乎不变,此时的光强分布也几乎不变.所以设计中小孔参数w应小于0.6 DL.类似的模拟显示,为了保持调制度在200 m范围内不变,圆形小孔半径需要小于0.6 DL,方形小孔边长的一半需要小于0.6 DL.考虑到实际上使用的小孔尺寸不能太小,所以通过调整透镜焦距使DL=1 mm.设计中,原光束宽度为0.04 m,在ISI分割数为4×4时,这要求图3中,f4=8 m,8×8时,f4=4 m,16×16时,f4=2 m.为了缩短系统长度,选取16×16的ISI分割数更好,同时,想要达到理想的匀滑效果,使用16×16的ISI分割数也是有必要的.此时有d67=220 m,只要w小于0.6 DL便能保证放大光路内光强分布不因传播而发生明显变化.

图4 0–200 m传播距离时调制度随小孔大小的变化(此时使用的小孔是高斯型小孔)Fig.4. Variations of modulation degree with size of aperture after propagation distance 0–200 m with Gaussian shape aperture used.

3.2 ISI分割数与小孔形状对近区光强分布的影响

以方形小孔为例,研究ISI分割数为4×4,8×8和16×16时,调制度、软化因子和透过率的变化.根据3.1节的结论,当小孔尺寸(方形小孔边长一半)小于0.6 DL时,光强分布几乎不随距离变化,所以选择小孔尺寸为0.2 DL–0.6 DL,其模拟结果见图5(a)–(c).可以看到使用相同的滤波孔,随着ISI数的增大,调制度变小,软化因子变小,透过率略微增大.根据调制度,使用不同ISI分割数时,最优的方形小孔尺寸都是0.4 DL.为了获得更好的近区均匀性与能量利用率,应当使用16×16的ISI分割.

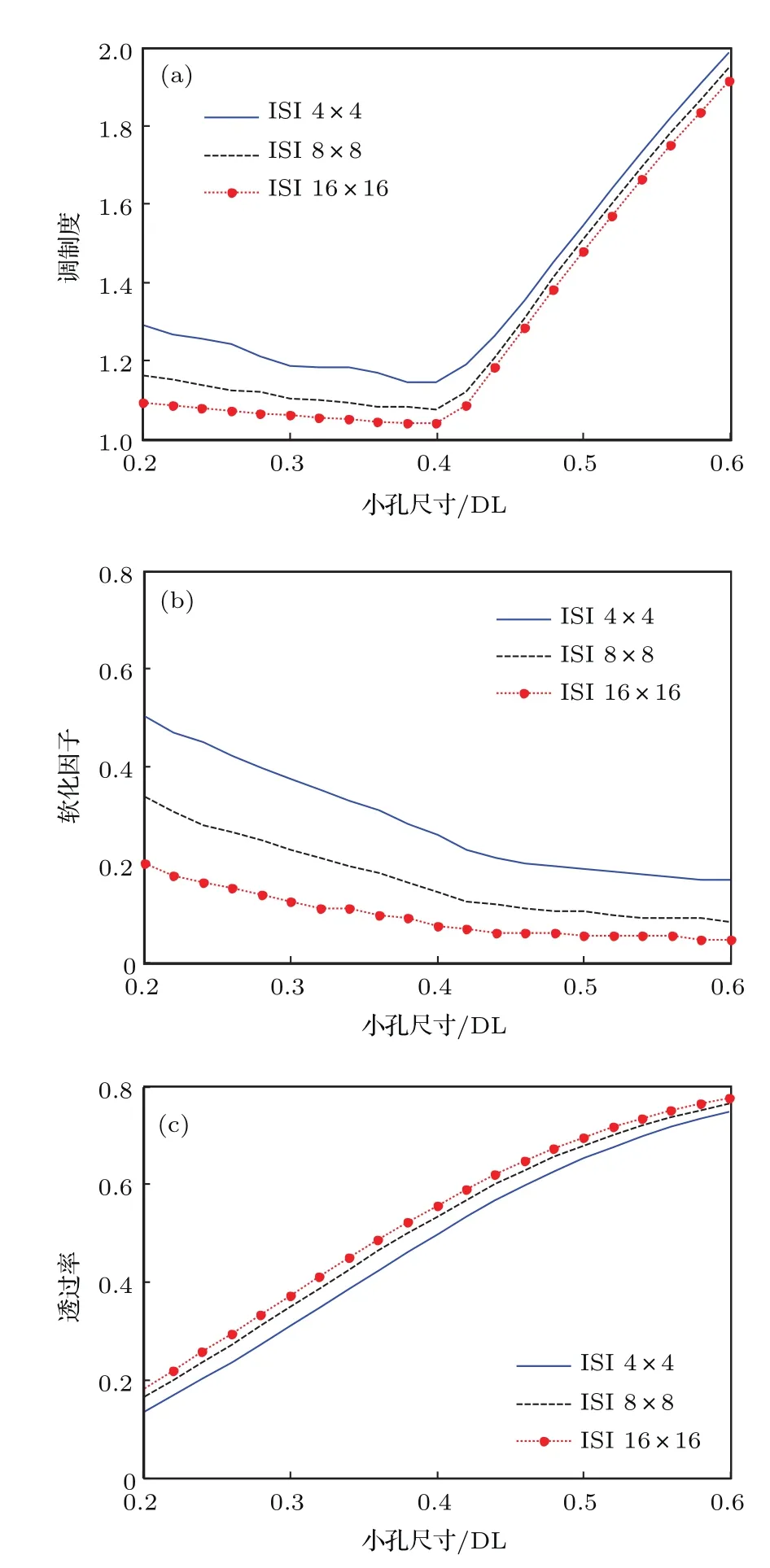
图5 在不同ISI分割数下 (a)调制度,(b)软化因子,(c)透过率随小孔尺寸的变化(其中小孔使用方形小孔)Fig.5.(a)Variations of modulation degree with size of aperture;(b)variations of softening factor with size of aperture;(c)variations of transmittance with size of aperture,with square apertures used here.

选取ISI分割数为16×16,对高斯形、圆形、方形3种不同的小孔形态的滤波效果进行研究.选取小孔尺寸在0.2 DL–0.6 DL间变化,为了维持低的不均匀性的同时减少损失能量,小孔尺寸应该选择在调制度快速增加的转折点上,计算结果如图6.

图6 (a)调制度随小孔尺寸的变化;(b)软化因子随小孔尺寸的变化;(c)透过率随小孔尺寸的变化Fig.6.(a)Variations of modulation degree with size of aperture;(b)variations of softening factor with size of aperture;(c)variations of transmittance with size of aperture.

图6(a)列出了对应这3种形态的小孔的调制度随小孔尺寸的变化.可以看出对不同的小孔形态,调制度达到最优所需的小孔尺寸有所不同.在小孔小时,3种情形调制度都接近为1.随着小孔半径的增加,使用高斯型软边小孔时,调制度在0.3 DL便开始快速增加,而使用另外两种小孔时,则在0.4 DL才开始增加.但高斯型小孔调制度增加得更慢.最终对高斯形、圆形、方形3种小孔选择小孔尺寸分别为0.3 DL,0.4 DL,0.4 DL,此时的中心区域调制度都小于1.1.图6(b)给出了软化因子与小孔尺寸的关系,其中的阶梯形状来自于有限的分辨率.软化因子随着小孔增大而减小.在图6(a)选取的最优小孔尺寸的3种情况下,其软化因子分别为0.11,0.10,0.08,其中方形小孔的数值最小.从图6(c)可以看出,对应3种类型的小孔,透过率都随着孔大小的增加而增加.3种最佳情况的透过率分别为0.17,0.48,0.56.其中方孔的透过率最高,而高斯型软边孔因0.3 DL的尺寸过小,透过率极低.这些结果被汇总在表1中.

根据以上模拟结果,相较其他情形,使用16×16的ISI分割数与宽度为0.8 DL的方形小孔,滤波后光束能够同时获得更好的均匀性、更陡的边缘与更高的透过率.

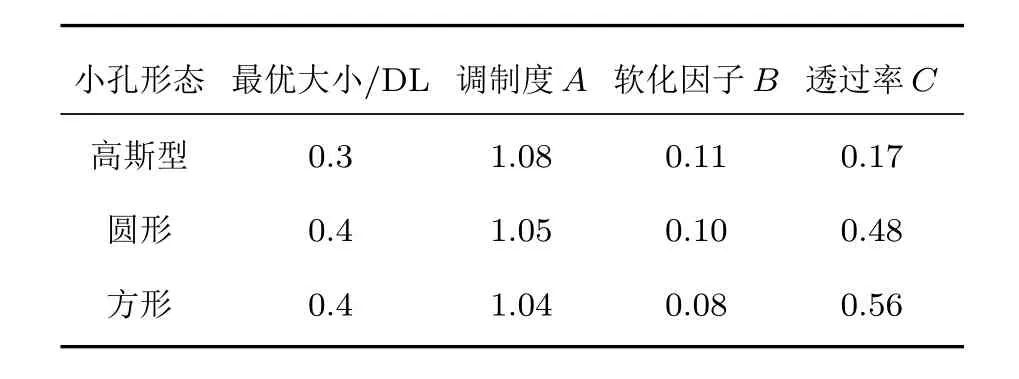
表1 不同形态小孔对应的近区强度分布参数比较Table 1.Comparison of intensity distribution parameters with different shapes of aperture at optimal aperture size.

3.3 准直误差对近区光强分布的影响

实际操作中,光束焦斑通过小孔5时可能会出现一定偏差,即准直误差.为了分析准直误差带来的影响,假设准直误差在x和y方向上分别为dξ,dη,这与将小孔偏置dξ,dη效果相同,即将(4)式中AP(ξ,η)替换为AP(ξ−dξ,η−dη).根据傅里叶变换平移定理,此时有

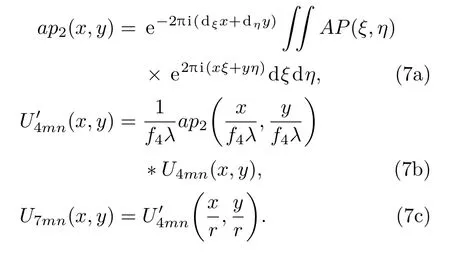
其中ap2(x,y)表示AP(ξ−dξ,η−dη)的二维傅里叶变换,其余符号含义与(4)式中相同.可见只需要在(4a)式的计算中额外乘一个相位因子,便能得到有准直误差的情况下的光场分布.只考虑一个方向上的误差,在最佳设计的基础上,对不同的准直误差量,计算近区分布评价参数,结果见图7.

图7 使用0.8 DL宽度方形小孔时(a)调制度,(b)软化因子,(c)透过率随准直误差的变化Fig.7.When using 0.8 DL square aperture:(a)Variations of modulation degree with offset of aperture;(b)variations of softening factor with offset of aperture;(c)variations of transmittance with offset of aperture.

由图7(a)可以看出,直到准直误差达到0.5 DL,调制度的增大都不明显,仅从1.04增大到了1.06,这意味着光束的近区均匀性保持良好.图7(b)显示了准直误差对软化因子的影响.在0.2 DL的准直误差内,软化因子增大不明显,继续增加准直误差,则软化因子开始加速增大,其阶梯形状来自于有限的分辨率.图7(c)表明透过率随着准直误差的增加而减小,当准直误差为0.1 DL时,透过率由0.56降低到0.54,约降低4%.综上所述,一直到0.1 DL的准直误差都不会明显影响近区均匀性与能量利用率.本文中设计使1 DL=1 mm,0.1 DL对应0.1 mm,准直误差小于此值是没有问题的.

3.4 滤波系统对ISI+CPP匀滑效果的影响

经过前面设计的双透镜滤波系统后,子光束形态变成了衍射斑状.对于ISI+CPP的匀滑方式,这意味着焦斑强度分布将会有所变化.假设图3进Gerchberg-Saxton(G-S)算法得到的CPP板,计算了使用ISI+CPP和使用ISI+CPP并加入空间滤波系统的两种情况下最终的焦斑形态,见图8,其中图8(a)和图8(c)是未使用空间滤波系统时的近区强度分布与焦斑,RMS=0.047,图8(b)和图8(d)是使用0.8 DL宽的方形滤波孔滤波系统时的近区强度分布与焦斑形态,RMS=0.018,图8(e)是两种情况的归一化空间谱强度.

图8 (a)无滤波系统时的近区分布;(b)使用最优空间滤波系统时的近区分布;(c)ISI+CPP,无滤波系统时的焦斑;(d)ISI+CPP,使用最优的空间滤波系统时的焦斑;(e)归一化空间谱强度Fig.8.(a)Near field intensity distribution without filter system;(b)near field intensity distribution with optimal filter system;(c)focal spot using ISI+CPP without spatial filter system;(d)focal spot using ISI+CPP with optimal spatial filter;(e)normalized spatial spectral intensity.

由图8(c)与图8(d)比较可发现,在使用滤波系统后,焦斑的不均匀性变低,同时强度调制转向了高频段.在图8(e)中也能观察到这种趋势.这是因为不使用滤波系统时,子光束强度分布集中在对应的小方形区域内,宽度小,所以远区散斑尺度大(横向散斑尺寸与近区宽度成反比).强度叠加后散斑尺度不会发生变化,所以高频调制不明显;同时大尺度的散斑更加难以通过强度叠加得到匀滑,所以此时焦斑中存在明显的低频不均匀性.而在增加滤波系统后,子光束呈衍射斑状,其分布范围变大,所以远区散斑尺度变小,小尺度的散斑的叠加效果更好,不均匀性向高频方向移动,整体均匀性更好,RMS变小.

4 结 论

为了降低诱导空间非相干技术引起的近区强度空间调制,本文提出了一种使用双透镜滤波系统消除ISI匀滑系统近区不均匀性的方法.通过理论计算与数值模拟,在3种滤波空形态中选择了最优设计.结果表明,与圆形小孔与高斯型软边小孔相比,使用宽度为0.8倍衍射极限的方形滤波孔时光束的近区调制度更低,软化因子更小,透过率更高.对准直误差的进一步模拟显示,控制光束准直误差在0.1倍衍射极限内便能保证近区光强分布均匀.使用双透镜滤波系统将影响到最终焦斑形态,计算表明,当使用ISI与G-S方法设计得到的常规连续相位板时,加入双透镜滤波系统能够获得均匀性更好的焦斑.