基于表面磁感应强度的铁磁构件应力恒磁表征方法∗
邓东阁 左苏 武新军
1)(华中科技大学机械科学与工程学院,武汉 430074)2)(中国工程物理研究院总体工程研究所,绵阳 621900)(2018年3月29日收到;2018年5月18日收到修改稿)
1 引 言
钢丝、钢棒等铁磁构件作为单元承载构件,广泛应用于桥梁、建筑等基础设施建设,方便快捷地获取铁磁承载构件应力状态对保证基础设施安全运行具有重要意义.目前应用较广泛的承载应力检测方法有[1]反拉法、振动频率法和电磁检测法等.其中,反拉法是通过张拉承载构件以确定荷载应力的方法[2],其检测原理相对简单,但检测过程繁杂费力且传感器耐久性较差.振动频率法[3]是通过测量固有振动频率,并根据固有频率与承载力之间的数学关系计算出构件承载力.其一般采用加速度传感器测量构件的固有频率,操作简便、成本较低,但检测结果容易受构件边界条件和垂度的影响.相比而言,电磁检测法具有传感器耐久性好、检测结果不受边界条件影响、可非接触检测构件实际应力值等优点,引起了国内外研究人员的广泛关注.
电磁检测方法[4]先通过测量不同应力下构件磁参数以标定出应力与特征磁参数间的关系方程,进而通过测量被测构件特征磁参数以反求其应力.因此,该方法的关键在于确定合适的应力表征磁参数.一方面,该磁参数可以提取于铁磁构件磁化曲线,这是因为铁磁构件磁化曲线会随其应力状态的不同而发生变化,被称为铁磁构件的磁弹效应.在磁弹效应理论研究方面,国外著名学者Sablik和Jiles[5−7]通过微观层面唯像地分析磁畴在磁化下的运动过程,并基于磁场和应力共同作用下材料内部能量最小原理,建立了J-A-S力磁耦合模型.该模型表明:同一磁场强度下,铁磁构件磁感应强度为关于应力的函数,会随应力σ的不同而变化;不同磁场强度下,磁感应强度随应力变化的灵敏度和线性度不同;因此,从理论模型层面难以准确快速地确定随应力变化的灵敏度高、线性度好的表征磁参数.在磁弹效应实际应用方面,国内外学者通过逐点分析来自于磁化曲线的磁参数如磁导率[8−11]、磁感应强度[12−14]等,来确定最佳的应力表征磁参数;相应的磁通量传感器[15,16]已开始用于实际应力检测.其一般在时变磁场线圈激励下,采用接收线圈拾取感应电压的方式获取该类磁参数;激励线圈和接收线圈需缠绕在被测构件上,实际应用不便,且存在长时激励线圈发热以及涡流影响检测结果的不足[10,17].我们曾提出基于恒定磁场激励的铁磁构件磁化曲线获取方法[18,19],该方法采用永磁恒定磁化器代替时变磁场线圈作为激励源,采用布置在铁磁构件表面的阵列磁敏感元件代替接收线圈来拾取构件表面轴向和法向磁感应强度,最终从基本磁学定理出发推算出构件磁化曲线,并进一步从磁化曲线上提取磁参数,用于铁磁构件应力检测[20,21].该方法可规避线圈缠绕、线圈发热及涡流效应影响的不足;但其在表面法向上需阵列布置多组磁敏感元件,测量不同提离下的轴向和法向磁感应强度,对阵列磁敏感元件的空间位姿要求较高.
另一方面,由于构件表面轴向磁感应强度同构件内部磁感应强度密切相关[13],浙江大学Duan等[17,22,23]提出采用构件表面轴向磁感应强度作为应力表征磁参数,采用磁电复合材料制成的磁敏感单元获取磁感应强度信号,从而避免接收线圈的缠绕难题.相应的磁电磁弹效应式传感器[24]也已开始应用于工程实际.但确定随应力变化率高、线性度好的表面磁感应强度仍较困难.这是由于铁磁材料磁学本构关系呈现非线性及矢量特性,不同磁场强度下表面磁感应强度随应力的灵敏度和线性度不同,目前仍缺乏相应的理论关系模型来指导应力表征磁参数的准确快速确立,实际操作时,主要采用缠绕在构件上的激励线圈产生时变磁场作为激励磁场,通过逐点分析法确定最佳应力表征磁参数,过程繁琐复杂,且无法规避激励线圈缠绕、发热及涡流影响检测结果的不足.
为此,本文在前期研究的基础上[18−21],提出基于表面磁感应强度的铁磁构件应力恒磁表征方法,采用永磁恒定磁化器产生全局衰减、局部均匀的空间变化磁场作为激励磁场,以消除时变磁场线圈激励带来的种种缺点;并在恒定磁场激励下建立铁磁构件表面轴向和法向磁感应强度关于应力导函数之间的关系方程,以快速确定合适的表面磁感应强度作为应力表征磁参数.本研究有望规避基于现有铁磁构件应力恒磁检测方法对阵列磁敏感元件空间位姿的严格要求,并简化最佳应力表征磁参数的确立过程,探索一种简便有效的铁磁构件应力检测方法.
2 铁磁构件应力恒磁表征的基本思想
铁磁构件应力恒磁表征[20,21]基本思想如图1所示.

图1 铁磁构件应力恒磁表征的基本思想框图Fig.1.The principle sketch for characterizing stress in ferromagnetic members using super ficial magnetic flux densities obtained from constant magnetizer.
图1中铁磁构件两端加载有轴向拉力,根据平面假设[25],在该载荷下,构件横截面变形前后始终保持为平面,且垂直于轴线,横截面中应力均匀分布.进一步分析构件应力状态可知,如果选择轴向z方向作为第一主应力方向,与z方向垂直的另外两方向作为第二、第三主应力方向,则除第一主应力外,其他主应力和切应力取值均为0.图中的应力σ即为选择轴向z方向作为第一主应力方向时的第一主应力.本文中所提出的铁磁构件应力检测方法适用于该载荷状态下的应力检测.其基本思想为:采用恒定磁场磁化器在铁磁构件上激励出随距磁化器长度L变化恒定磁场B=f(L),该恒定磁场满足全局衰减、局部均匀正交分布条件[20,21].所谓全局衰减是指恒定磁场B随距磁化器长度L的增大而不断衰减,局部均匀是指同一轴向位置L处,铁磁构件横截面内的恒定磁场强度是均匀相等的.在满足此条件下,在不同轴向位置L处布置磁敏感单元,测得不同L处同一提离Lo下的法向磁感应强度和轴向磁感应强度反映了应力σ作用下铁磁构件在不同磁场强度作用下的磁参数.因此,从不同L处的中,可提取出需随应力变化率高、线性度好的表面磁感应强度值,作为铁磁构件应力最佳表征磁参数,以方便铁磁构件应力的标定和检测.下文重点阐述基于表面磁感应强度的应力表征原理,以准确、高效地从不同L处的中确定铁磁构件应力最佳表征磁参数.
3 基于表面磁感应强度的应力表征原理
铁磁构件表面磁感应强度关于应力的导函数直接反映表面磁感应强度随应力的变化率[26].因此,为快速确定随应力变化率高的表面磁感应强度,本节先建立铁磁构件表面内外轴向磁感应强度关于应力导函数之间的关系方程,然后结合我们推导的铁磁构件表面法向磁感应强度与构件内部轴向磁感应强度关系方程[18,19],最终建立铁磁构件表面轴向和法向磁感应强度关于应力导函数和之间的关系,据此为快速确定铁磁构件表面轴向和法向磁感应强度随应力变化的灵敏度极值点提供理论支撑.
3.1 内外轴向磁感应强度关于应力导函数之间的关系
内外轴向磁感应强度关于应力导函数之间的关系通过退磁场理论和磁场强度切向连续性确定.首先分析外加磁场Hs(L)下,轴向位置L至L+dL段铁磁构件内外磁场分布,如图2所示.
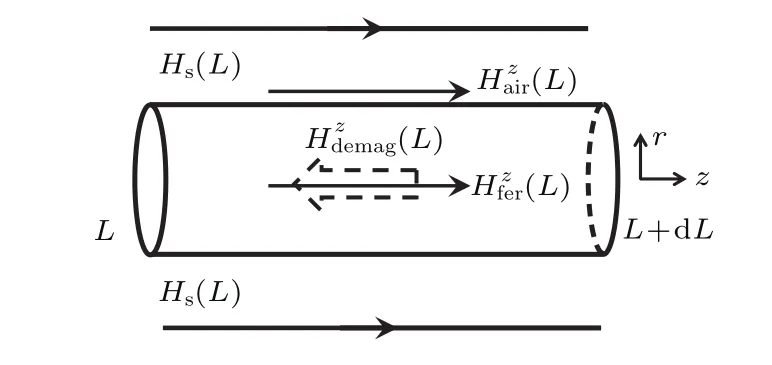
图2 外加磁场Hs(L)作用下铁磁构件内外磁场分布Fig.2.Magnetic field distribution inside and outside of the ferromagnetic member under external magnetic field Hs(L).
由退磁场理论[27,28]可知,外加磁场Hs(L)作用下铁磁构件内实际磁场强度与退磁场叠加作用的结果,可表示为


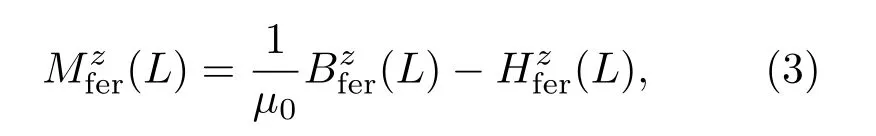
其中µ0为真空磁导率.综合(1)—(3)式可得,实际磁场强度与Hs(L)及磁感应强度的关系式

进一步地,由磁场强度切向连续性可知,构件表面空气中的磁场强度与构件中的磁场强度有如下关系[29]:
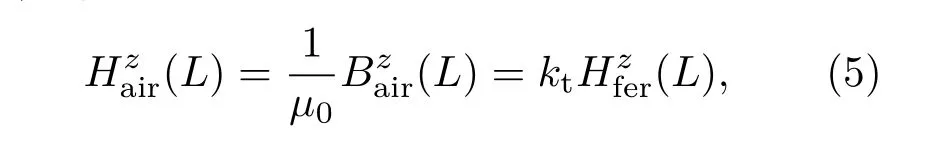
其中kt为只与构件形状相关的常数,综合(4)和(5)式,可得铁磁构件内外磁感应强度关系式
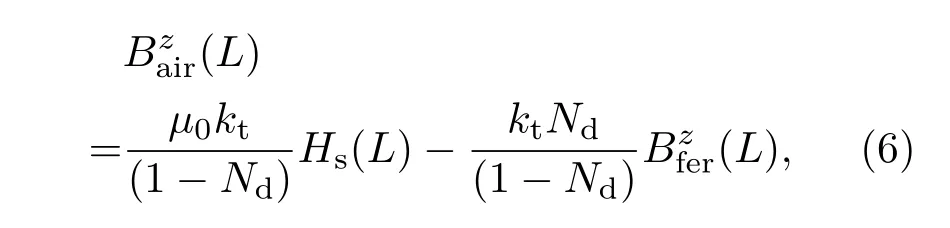
(6)式中系数kt和退磁系数Nd只与构件形状相关,外加磁场Hs(L)也可认为不随应力σ变化,而根据J-A-S模型可知,(6)式中随应力σ的不同而改变,故是关于应力σ的函数.则(6)式可做关于应力σ的偏微分得

其中kz为常数,其值为ktNd/(1−Nd).由(7)式可知,同一测点处铁磁构件内外轴向磁感应强度同应力的偏导数呈负相关:即同一测点处内外磁感应强度随应力变化的灵敏度相同但趋势相反.
3.2 表面轴向和法向磁感应强度关于应力导函数之间的关系
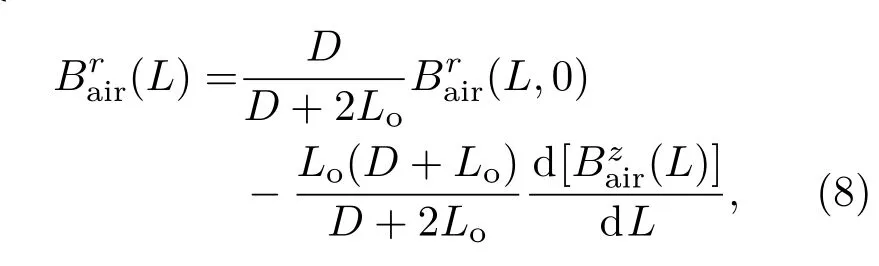
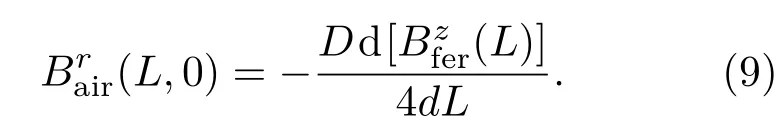
综合(8)和(9)式可得如下关系式:
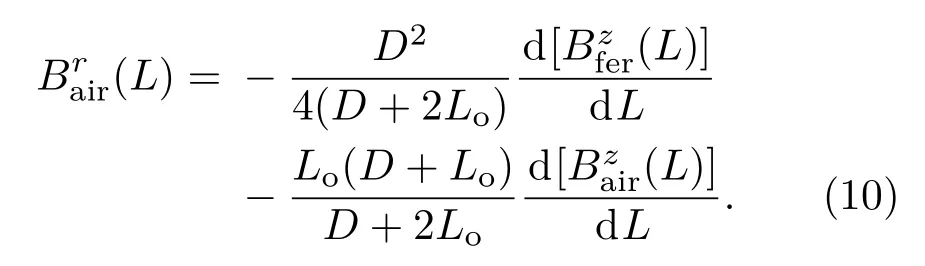
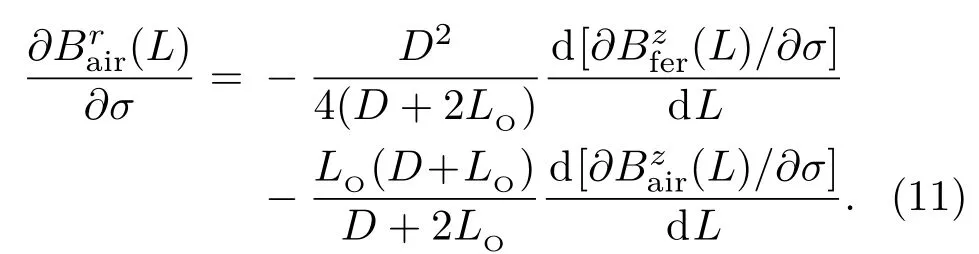
结合(11)式和(7)式可得铁磁构件表面轴向和法向磁感应强度关于应力导函数和之间关系为
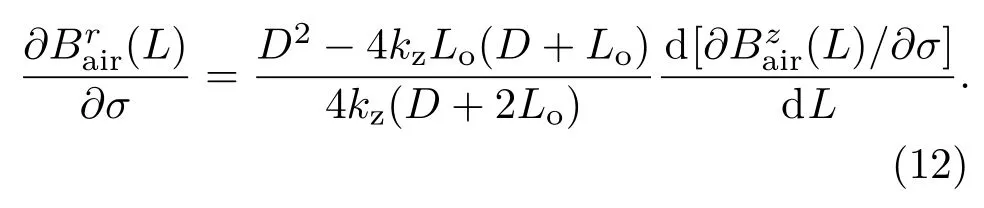
分析(12)式可知,构件表面轴向和法向磁感应强度关于应力导函数均是随轴向位置L变化的函数,反映了轴向和法向磁感应强度随应力变化的灵敏度.如将其分别记为则有

到以下结论:
4 实验验证
本节搭建铁磁构件应力恒磁检测实验系统,以研究恒定磁场激励下基于表面磁感应强度的应力表征原理的正确性,进一步确立基于表面磁感应强度的铁磁构件应力恒磁表征方法.
4.1 实验系统
基于表面磁感应强度的铁磁构件应力恒磁检测实验系统布置如图3所示.该实验系统主要由被测构件、加载装置、压力传感器、轴力计、永磁激励单元、正交磁场测量单元和FLUKE万用表等组成.其中,被测构件采用SWRS82B高强度钢制成的Φ5及Φ7钢丝和45#钢制成的Φ20钢棒,以验证基于表面磁感应强度应力表征原理对不同材料不同尺寸构件的普适性.钢丝和钢棒构件所用永磁激励单元尺寸分别见文献[17,18],以在钢丝和钢棒上产生满足全局衰减局部均匀的空间变化磁场.正交磁场测量单元[18]由MICRONAS公司TO92UA封装的高精度线性HAL1823元件制成.

图3 基于表面磁感应强度的铁磁构件应力恒磁表征实验布置图Fig.3.Layout diagram for the experiment characterizing axial stress in ferromagnetic members using super ficial magnetic flux density obtained from static magnetization by permanent magnets.
实验时,被测构件通过左侧固定螺母和右侧加载螺母锚固在加载装置上,加载装置主要由加载架、支撑架、止转轭、挡板和推力轴承等组成.旋紧加载螺母可对构件施加轴向拉力F,在此过程中,止转轭可防止构件旋转.轴向拉力通过YLR-3 FK压式负荷传感器监测并显示在YJZ-500 A型轴力计上;其中YLR-3 FK压式负荷传感器的最大测量范围为500 kN,YJZ-500 A型轴力计的精度等级为1级;通过计量部门检定其检测精度为±1.0%[30].将永磁激励单元和正交磁场测量单元通过一平行导轨相连接,并放置在被测构件上.永磁激励单元中心距离被测构件右端部1000 mm,在被测构件上激励出随轴向位置变化的恒定磁场;空间正交磁场测量单元和滑块一起,沿平行导轨左右滑动以感应被测构件不同轴向位置处的表面磁感应强度.具体而言,磁场测量单元中封装的霍尔芯片将被测构件表面1.5 mm提离下的磁感应强度信号转换为电压信号,并将其传送给FLUKE五位半万用表;记录各测点万用表的电压值读数再结合HAL1823芯片的灵敏度,来换算被测构件表面1.5 mm提离下的法向和轴向磁感应强度和最后,根据第3节所述,从所测法向和轴向磁感应强度中,快速确定灵敏度最高的应力表征磁参数,并拟合出其与应力变化关系的线性度,以验证基于表面磁感应强度的应力表征原理的可行性.
4.2 铁磁构件应力表面磁感应强度表征实验结果
铁磁构件应力表面磁感应强度表征实验内容如表1所列.

表1 铁磁构件应力表面磁感应强度表征实验内容Table 1.The contents of the experiment characterizing axial stress in ferromagnetic members using super ficial magnetic flux density.
采用柳州欧维姆机械股份有限公司提供的同一批次三根Φ5钢丝和三根Φ7钢丝以及无锡卓诚五金机电有限公司提供的同一批次三根Φ20钢棒作为试样.钢棒横截面较钢丝大,钢棒试件施加拉应力范围及步长与钢丝试件也不相同.实验时,分别检测400—800 MPa(加载步长为50 MPa)钢丝表面1.5 mm提离下以及0—382.0 MPa(加载步长为95.5 MPa)钢棒表面1.5 mm提离下的轴向和法向磁感应强度每次加载后均重复检测三次.实验测得的1号Φ5及Φ7钢丝和Φ20钢棒表面轴向及法向磁感应强度和三次测量平均值随应力的变化关系分别如图4、图5及图6所示.
整体分析可知,L较小时钢丝和钢棒中磁场强度较大,随应力的增大而增大;而L较大时钢丝和钢棒中磁场强度较小,随应力的增大而减小.钢丝和钢棒表面轴向磁感应强度与内部轴向磁感应强度随应力的变化趋势[20,21]相反,这证明了上述“基于表面磁感应强度的应力表征原理”的正确性.

图4 1号Φ5钢丝表面轴向(a)及法向(b)磁感应强度三次测量平均值随钢丝应力的变化Fig.4.The relationships of the stress with the average axial(a)and normal(b)magnetic flux densities of the three measurement data from the first Φ5 mm steel wire.
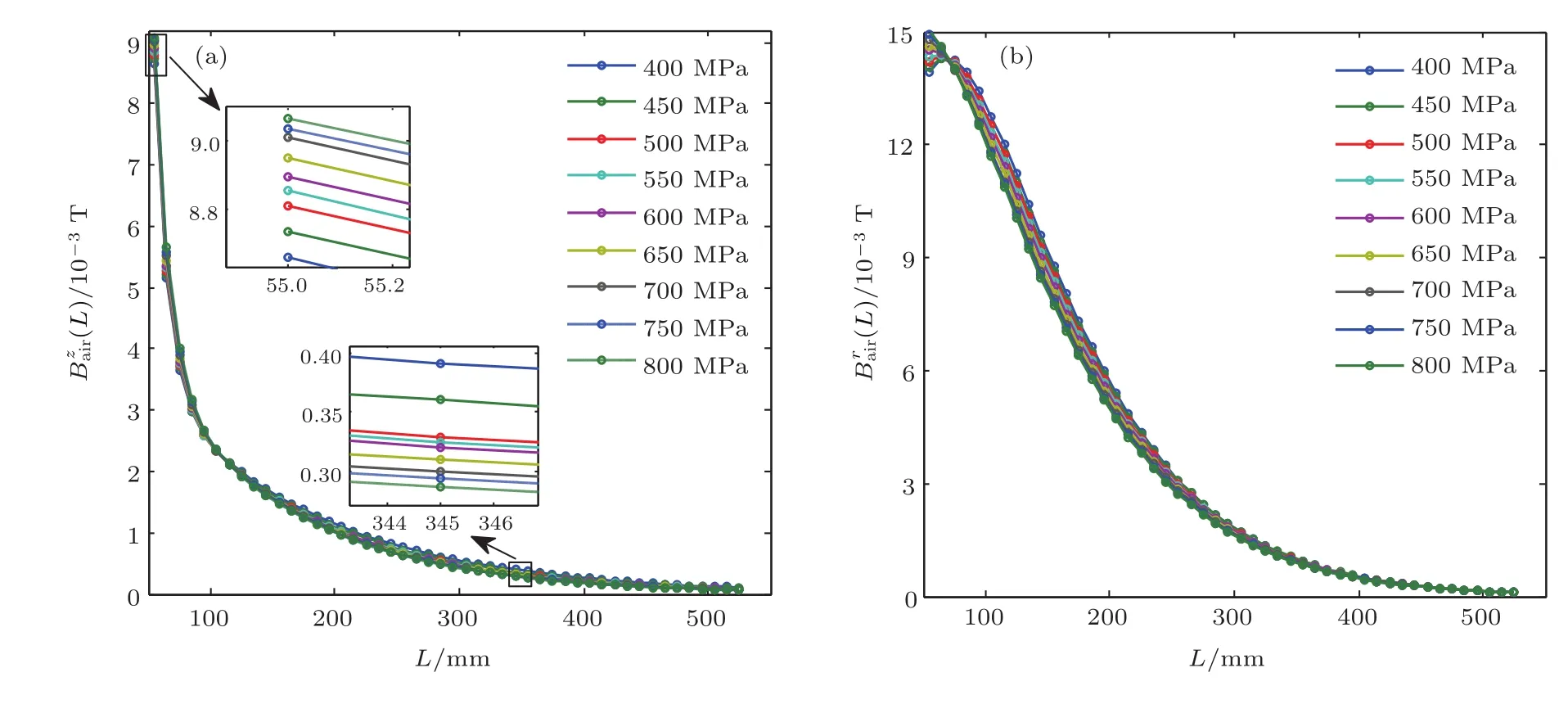
图5 1号Φ7钢丝表面轴向(a)及法向(b)磁感应强度三次测量平均值随钢丝应力的变化Fig.5.The relationships of the stress with the average axial(a)and normal(b)magnetic flux densities of the three measurement data from the first Φ7 mm steel wire.
细致分析可知,不同轴向位置L处钢丝和钢棒表面轴向及法向磁感应强度随应力变化的灵敏度不同;原理上讲,灵敏度最高点在检测区间的端部或者检测区间内灵敏度极值点处取得;基于第3节所述及实际检测数据,确定钢丝和钢棒表面轴向磁感应强度中随应力的灵敏度为最高,而钢丝和钢棒随应力的灵敏度最高的法向磁感应强度分别为和

图6 1号Φ20钢棒表面轴向(a)及法向(b)磁感应强度三次测量平均值随钢棒应力的变化Fig.6.The relationships of the stress with the average axial(a)and normal(b)magnetic flux densities of the three measurement data from the first Φ20 mm steel bar.
下面进一步比较上述参数随应力的变化率及线性度,以分析其作为钢丝和钢棒应力表征磁参数的可行性.为此线性拟合上述参数随应力变化关系,得到Φ5及Φ7钢丝和Φ20钢棒表面灵敏度最高的轴向和法向磁感应强度随应力的变化关系,分别如图7、图8和图9所示.
图7、图8和图9分别显示了三根Φ5钢丝、三根Φ7钢丝和三根Φ20钢棒三次重复检测数据的平均值、最小值和最大值.分析可知,同一批不同编号的钢丝和钢棒的磁感应强度检测值基本一致;所选磁感应强度同应力近似呈线性变化.为定量分析各磁感应强度随应力的变化关系,用线性拟合优度R2代表各磁感应强度与随应力变化的线性度;计算加载区间内各磁感应强度的相对变化率绝对值η,以分析各磁感应强度对应力σ的灵敏度.则不同编号Φ5及Φ7钢丝和Φ20钢棒表面轴向和法向磁感应强度与应力σ变化关系的拟合结果分别如表2、表3和表4所列.
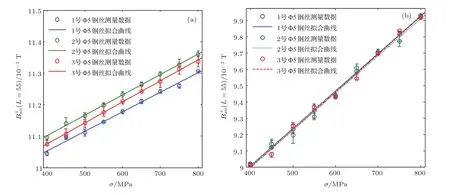
图7 Φ5钢丝(a)轴向磁感应强度(L=55)和(b)法向磁感应强度(L=55)随应力的变化Fig.7.The relationships of the stress with the axial magnetic flux density(L=55)(a)and normal magnetic flux density(L=55)(b)measured from three Φ5 mm steel wires.
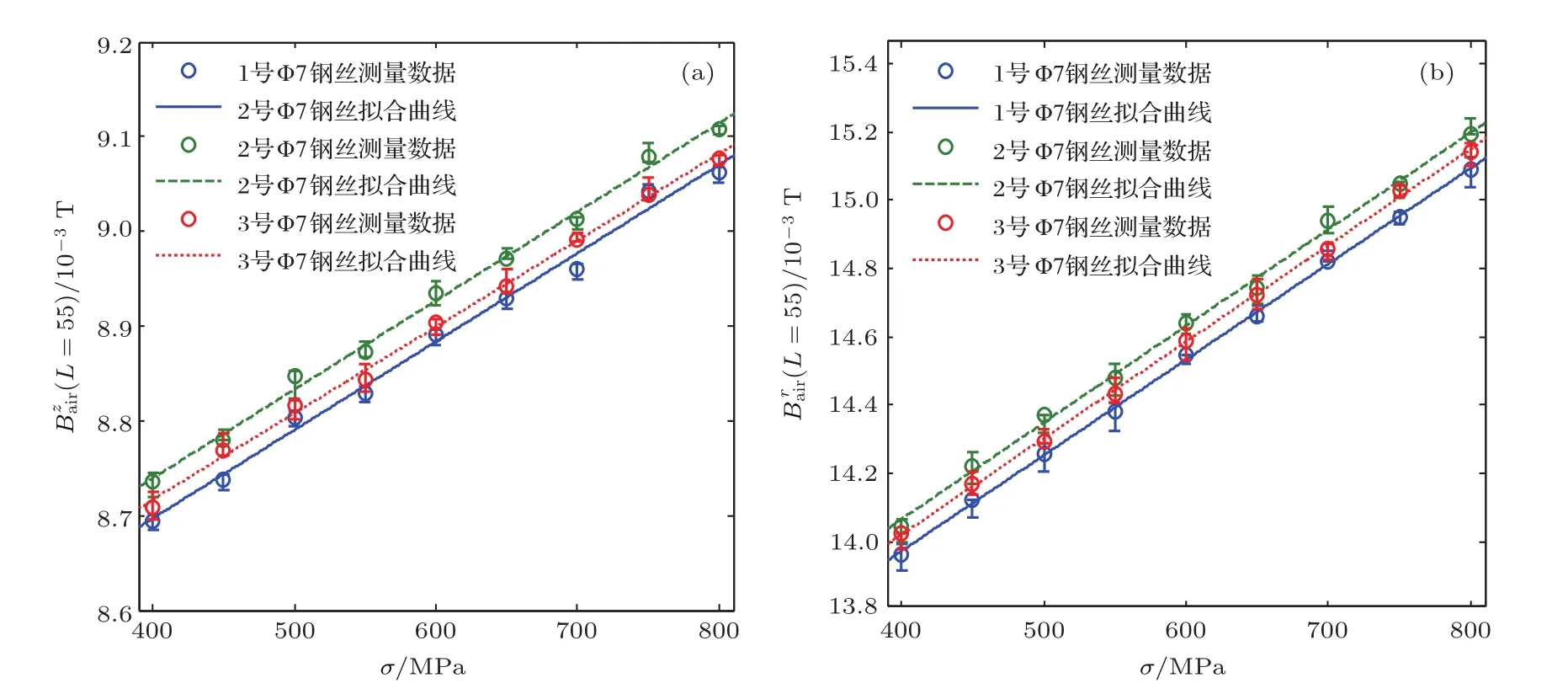
图8 Φ7钢丝(a)轴向磁感应强度和(b)法向磁感应强度随应力的变化Fig.8.The relationships of the stress with the axial magnetic flux density(a)and normal magnetic flux density(b)measured from three Φ7 mm steel wires.
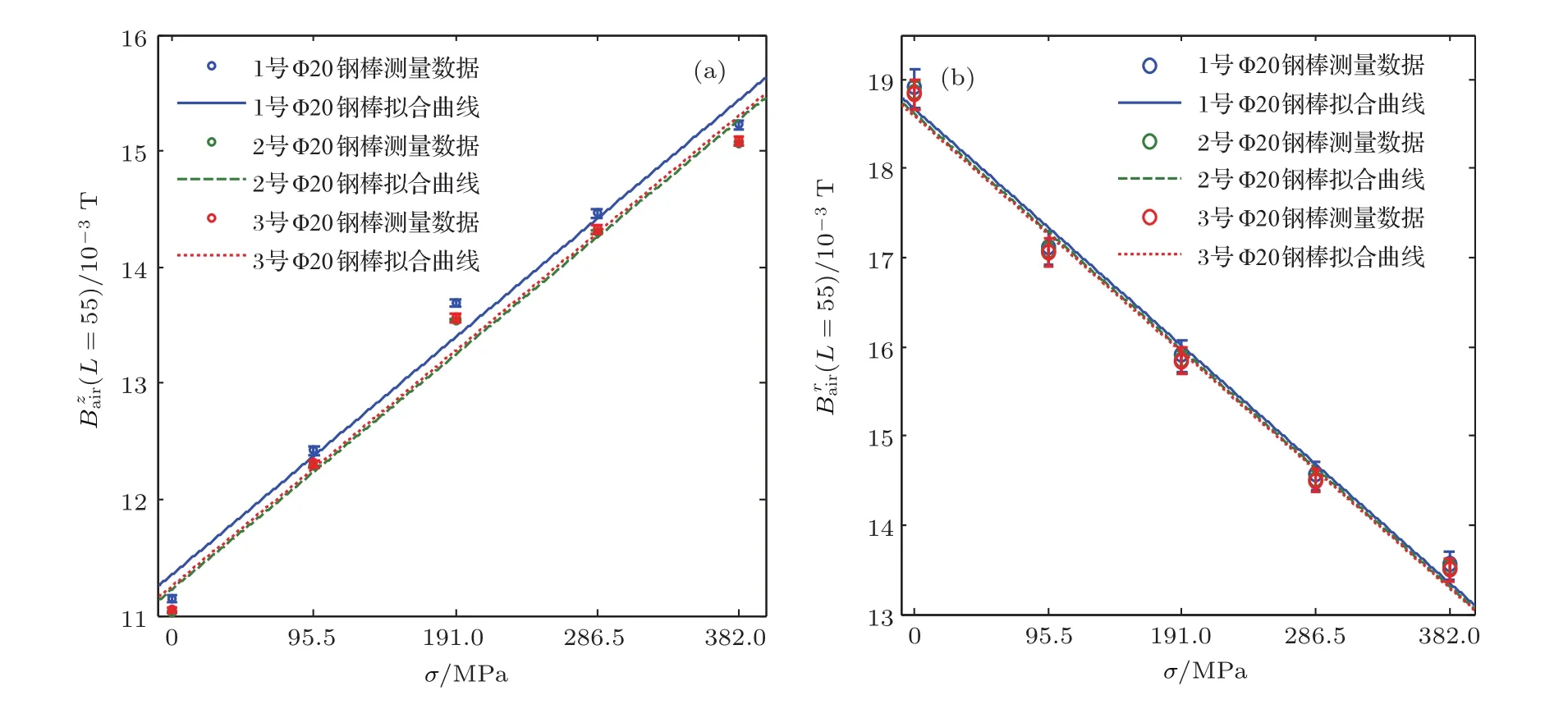
图9 Φ20钢棒(a)轴向磁感应强度(b)法向磁感应强度随应力的变化Fig.9.The relationships of the stress with the axial magnetic flux density(a)and normal magnetic flux density(b)measured from three Φ20 mm steel bars.
表2 不同编号Φ5钢丝表面磁感应强度(L=55)同应力σ变化关系的拟合结果Table 2.The fitting results for the relationships between the sur ficial magnetic flux densitiesandmeasured from three Φ5 mm steel wires.

表2 不同编号Φ5钢丝表面磁感应强度(L=55)同应力σ变化关系的拟合结果Table 2.The fitting results for the relationships between the sur ficial magnetic flux densitiesandmeasured from three Φ5 mm steel wires.
试件编号 特征参数 拟合函数 R2 η/%1号 Bzair(L=55) Bzair(L=55)=6.2148× 10−7σ+1.0804 × 10−2 0.9925 2.25 Brair(L=55) Brair(L=55)=2.3058× 10−6σ+8.0834 × 10−3 0.9986 10.24 2号 Bzair(L=55) Bzair(L=55)=6.4694× 10−7σ+1.0843 × 10−2 0.9988 2.33 Brair(L=55) Brair(L=55)=2.2825× 10−6σ+8.0860 × 10−3 0.9921 10.15 3号 Bzair(L=55) Bzair(L=55)=6.6807× 10−7σ+1.0808 × 10−2 0.9990 2.41 Brair(L=55) Brair(L=55)=2.3245× 10−6σ+8.0650× 10−3 0.9933 10.34
表3 不同编号Φ7钢丝表面磁感应强度与应力σ变化关系的拟合结果Table 3.The fitting results for the relationships between the sur ficial magnetic flux densities Bzair(L=55)andmeasured from three Φ7 mm steel wires.

表3 不同编号Φ7钢丝表面磁感应强度与应力σ变化关系的拟合结果Table 3.The fitting results for the relationships between the sur ficial magnetic flux densities Bzair(L=55)andmeasured from three Φ7 mm steel wires.
试件编号 特征参数 拟合函数 R2 η/%1号 Bzair(L=55) Bzair(L=55)=9.3363× 10−7σ+8.3232 × 10−3 0.9919 4.29 Brair(L=55) Brair(L=55)=2.8020× 10−6σ+1.2851 × 10−2 0.9993 8.02 2号 Bzair(L=55) Bzair(L=55)=9.3700× 10−7σ+8.3643 × 10−3 0.9957 4.29 Brair(L=55) Brair(L=55)=2.8292× 10−6σ+1.2934 × 10−2 0.9978 8.05 3号 Bzair(L=55) Bzair(L=55)=9.1322× 10−7σ+8.3510 × 10−3 0.9970 4.19 Brair(L=55) Brair(L=55)=2.8214× 10−6σ+1.2892× 10−2 0.9993 8.05
表4 不同编号Φ20钢棒表面磁感应强度与应力σ变化关系的拟合结果Table 4.The fitting results for the relationships between the sur ficial magnetic flux densities Bzair(L=55)andmeasured from three Φ20 mm steel bars.

表4 不同编号Φ20钢棒表面磁感应强度与应力σ变化关系的拟合结果Table 4.The fitting results for the relationships between the sur ficial magnetic flux densities Bzair(L=55)andmeasured from three Φ20 mm steel bars.
试件编号 特征参数 拟合函数 R2 η/%1号 Bzair(L=55) Bzair(L=55)=1.0692× 10−5σ+0.0113 0.9833 35.98 Brair(L=165) Brair(L=165)= −1.3909× 10−5σ+0.0187 0.9904 28.46 2号 Bzair(L=55) Bzair(L=55)=1.0573× 10−5σ+0.0112 0.9836 35.97 Brair(L=165) Brair(L=165)= −1.3869× 10−5σ+0.0186 0.9910 28.43 3号 Bzair(L=55) Bzair(L=55)=1.0598× 10−5σ+0.0113 0.9830 35.96 Brair(L=165) Brair(L=165)= −1.3848× 10−6σ+0.0186 0.9907 28.49
分析表2—表4可知,在第3节“基于表面磁感应强度的应力表征原理”指导下确定的表面磁感应强度不仅灵敏度较高,线性度也较好,其同应力σ变化关系的拟合优度R2均大于0.98.根据该原理稍加分析可确定,针对SWRS82B钢丝构件,宜采用法向磁感应强度表征其应力;而针对45#钢的钢棒构件,宜采用轴向磁感应强度表征其应力.因此,基于表面磁场感应强度的铁磁构件应力恒磁检测方法是可行的.
5 结 论
本文提出了一种基于表面磁感应强度的铁磁构件应力恒磁表征方法,着重阐述了恒定磁场激励下基于表面磁感应强度的应力表征原理.该方法不仅可避免时变磁场激励所带来的线圈缠绕、线圈发热、涡流影响检测结果的不足,无需在径向布置多组空间位姿要求严格的磁敏感元件阵列;而且可根据提出的应力表征原理快速准确地确定被测构件表面随应力变化灵敏度最高的磁感应强度.实验结果表明,该应力恒磁检测方法适用于不同直径、不同材料铁磁构件均匀应力的检测,由“基于表面磁感应强度的应力表征原理”所确定的构件表面磁感应强度不仅灵敏度高、线性度也较好.该方法为铁磁构件工作应力检测提供了一种新途径.

