基于ANP-SD的地铁系统脆弱性仿真分析
郝倩雯,郭庆军,贾 哲
(西安工业大学建筑工程学院,西安 710021)
我国城市地铁建设规模和数量持续扩大,截至2016年末,中国大陆地区有48个城市在建轨道交通线路总长5 636.5 km,在建线路228条,地铁建设已经进入快速发展时期。由于环境多变、工人和设备受各方面影响,易出现较大的工作失误,导致地铁系统呈现出复杂性和非线性特征[1],而地铁系统自身存在较大的脆弱性。同时,地铁事故频发致使地铁安全管理成为国内外研究热点。
目前国内外关于脆弱性的研究较多,多围绕城市轨道交通、城市物流领域和城市公共安全等方面展开。李启明等[2]运用解释结构模型(ISM)和交叉影响矩阵相乘法(MICMAC)构建驱动力—依赖度象限图,将脆弱因子进行分类。吴贤国[3]提出一套基于复杂网络理论的地铁线网脆弱性分析方法,系统分析随机攻击和蓄意攻击模式下城市地铁网络的静态与动态脆弱性水平。成虎和韩愈[4-5]构建地铁系统脆弱性的脆弱链模型,进行基于功能和界面关系的脆弱性分析;基于脆弱性理论和耗散结构理论,提出着眼于脆弱性的地铁运营安全事故致因理论。李书全[6]建立基于BP-SD的施工企业安全系统脆弱性动力学仿真模型,探究各子系统对敏感性和应对能力的影响情况。许葭、宋守信建立基于网络层次分析法(ANP)的网络脆弱性评价模型[7],对地铁网络各站点脆弱性进行评估。宫剑[8]利用地铁拓扑结构和运营客流分布,提出基于层次分析法(AHP)的站点脆弱性评价方法,定量分析各站点脆弱性。
在对现有研究进行分析之后,笔者着重考虑系统内部存在的复杂反馈关系和系统自身固有的非线性动态特性。通过网络层次分析法(ANP)和系统动力学(SD)两种理论的结合,构建基于ANP权重计算值的系统动力学(SD)仿真模型,探究地铁脆弱性影响因素体系各因素对脆弱性的影响水平,构建地铁系统各因素内在反馈关系,模拟分析安全投入对脆弱性的影响趋势和各因素对脆弱性影响水平,从而为地铁安全管理提供建议,提升地铁安全管理效率和安全管理水平。
1 地铁系统脆弱性影响因素体系的构建
1.1 地铁系统脆弱性内涵
脆弱性最早起源于对环境科学的研究[9],后被引入物流、城市交通和道路运输系统等领域。关于脆弱性的定义并没有一个统一的界定,在自然科学领域,脆弱性是自然、动植物、动植物群体、社会、国家、制度等众多属性中部分属性的集合,是表示事物应对波动性、随机性、压力等的变化趋势;在安全领域,安全系统脆弱性是指安全系统在遭受外界扰动时表现出的敏感性和应对能力[9]。脆弱性作为系统的一种固有属性[10],有别于能够容纳、抵抗或处理系统内不确定性变化的能力水平的系统柔韧性;维持、恢复和优化系统安全状态能力的安全韧性;系统抵抗外部环境干扰和内部不确定性因素影响而能保持稳定工作能力的安全系统鲁棒性[11-13]。在地铁系统中,脆弱性是指系统固有的一种属性,是影响地铁系统安全性和可靠性的薄弱环节,并当系统暴露在干扰下时,抵抗外界干扰与障碍能力不足而由此可能造成地铁系统安全隐患的特性。因此,可以从人-机-环-管四个方面对地铁系统脆弱性进行影响因素的分析与研究,从而探究地铁系统脆弱性对系统整体的影响。
1.2 地铁系统脆弱性影响因素体系
地铁系统作为一个开放、动态的复杂系统,系统内各影响要素众多且相互作用,影响系统正常运行。借鉴已有研究[2],对通过文献调研和专家访谈筛选出的地铁系统脆弱性影响因素进行人-机-环-管四要素分类,形成地铁系统脆弱性影响因素体系,如图1所示。

图1 地铁系统脆弱性影响因素体系
地铁系统脆弱性影响因素体系由两层指标组成,第一层为人员脆弱性、设备脆弱性、环境脆弱性和管理脆弱性,第二层为人员技术业务水平、人员的安全意识、人员的自身素质、人员的身心状态、设施设备状态、设施设备性能、设施设备防护、设施设备的关联性、自然环境、社会环境、运营环境、路网拓扑结构、教育培训、规章制度、组织结构、应急管理计划、应急处置效率和应急资源保障。各影响因素在地铁系统中存在一定的相互关系并相互作用、相互影响,因此可以利用网络层次分析法(ANP)对各影响因素进行结构模型的构建和指标权重的确定,以识别各影响因素在地铁系统脆弱性影响因素体系中的重要度。
2 基于ANP的地铁系统脆弱性各影响因素权重的确定
2.1 构造ANP典型网络结构
网络层次分析法(ANP)是Saaty教授在提出网络层次分析法(AHP)之后于1996年提出的一种多准则决策方法。ANP是AHP的拓展和延伸,主要针对决策问题结构具有依赖性和反馈性的情况,目前多围绕效益、成本、机会、风险展开[14]。在地铁系统脆弱性影响因素体系中,体系中各影响因素存在依赖关系和反馈关系,所以采取传统层次分析法并不能有效反映其内在联系,故选用ANP计算地铁系统脆弱性影响因素体系中各指标权重。
ANP的典型结构描述由两大部分组成,分别为控制层和网络层。根据图1构建地铁系统脆弱性影响因素体系ANP结构模型,如图2所示。在ANP结构中Ci(1,2,3,4)为一级指标,Cij(i=1,2,3,4;j=1,2,3,4,5,6)为二级指标。
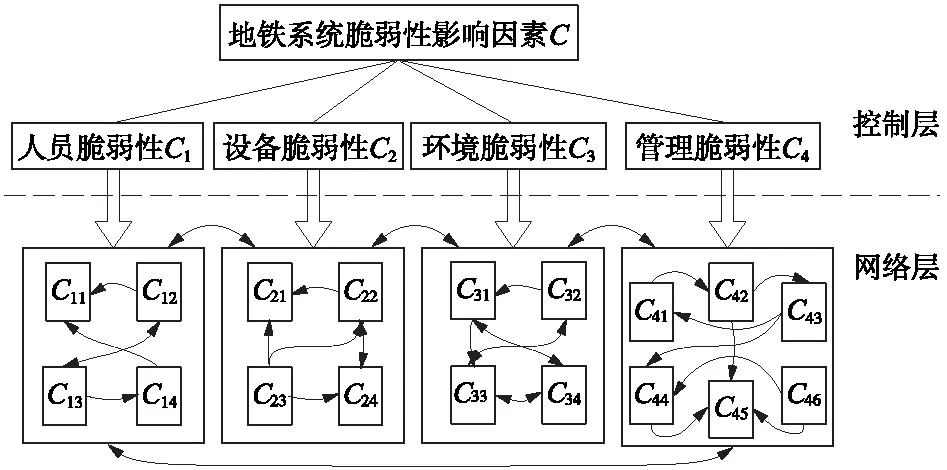
图2 地铁系统脆弱性影响因素体系ANP结构模型
2.2 地铁系统脆弱性影响因素指标权重计算
ANP进行指标计算的核心步骤是超矩阵运算,其运算过程十分复杂,故需借助超级决策软件(Super Decisions)进行计算[15]。超级决策软件(Super Decisions)是由Rozann Satty和William Adams共同研发,是基于ANP理论的一款强大的ANP计算工具[16]。在分析地铁系统脆弱性影响因素体系中各因素之间的内在关系后(图2),邀请7名专家,其中1名教授,2名副教授,3名地铁工作人员,对各组、各要素进行打分,形成两两对比矩阵。然后用超级决策软件构建ANP模型,并进行数据输入,依次得到矩阵、加权超矩阵、极限超矩阵,从而完成指标权重的计算,运算结果如表1、表2所示。最后整理结果如表3所示。
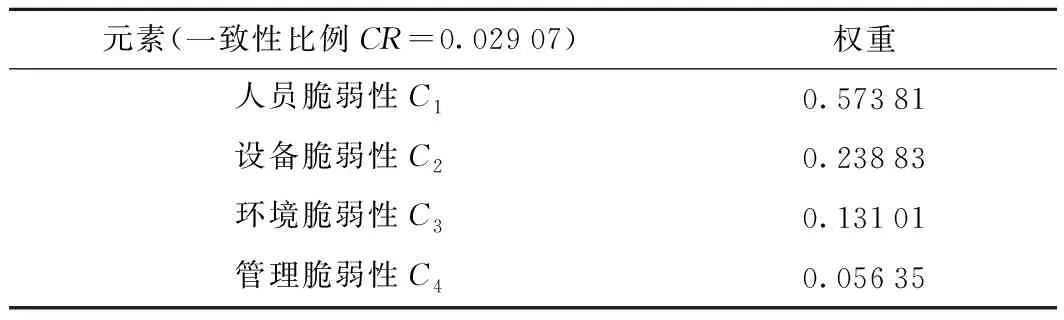
表1 地铁系统脆弱性影响因素体系ANP结构模型一级指标权重计算结果
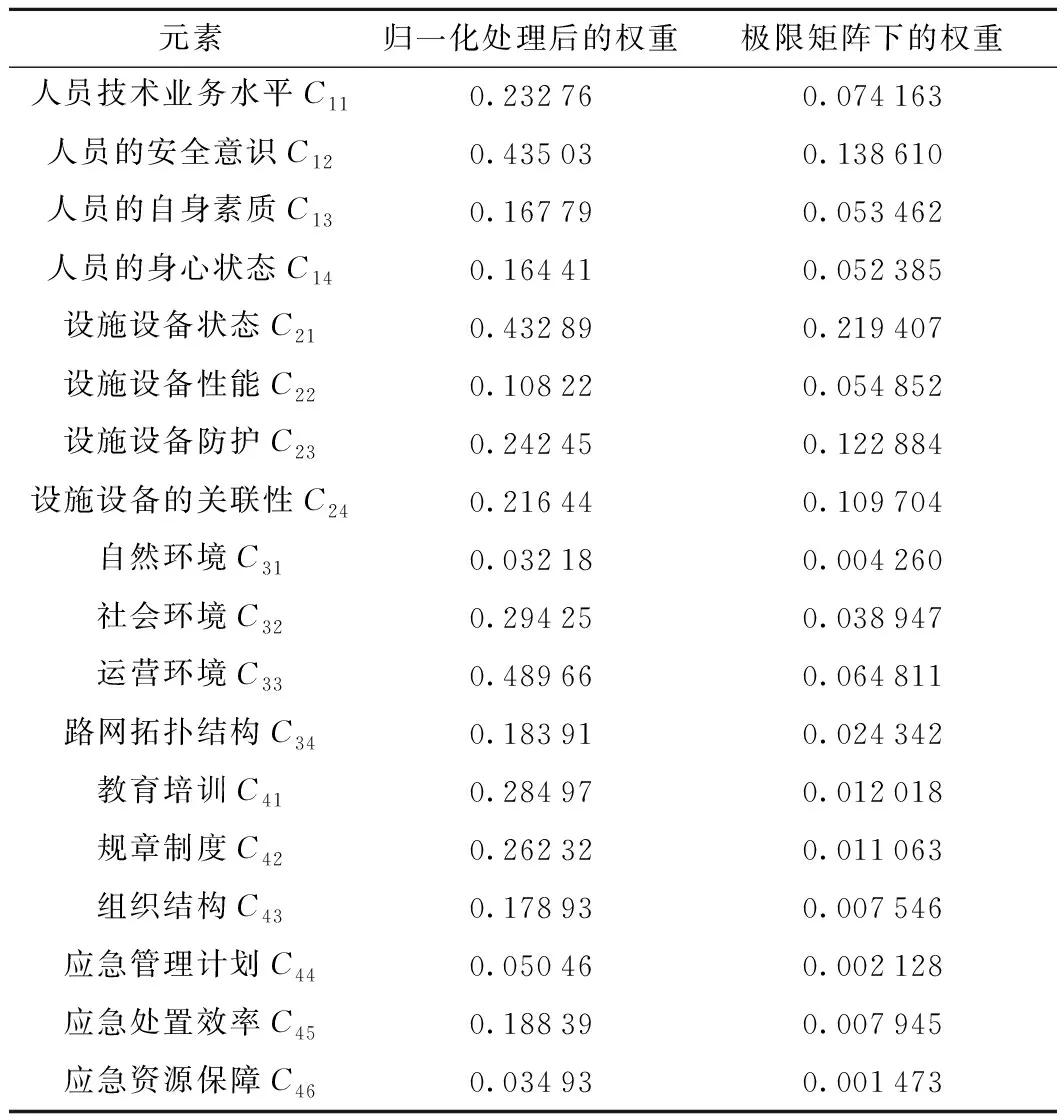
表2 地铁系统脆弱性影响因素体系ANP结构模型权重计算结果
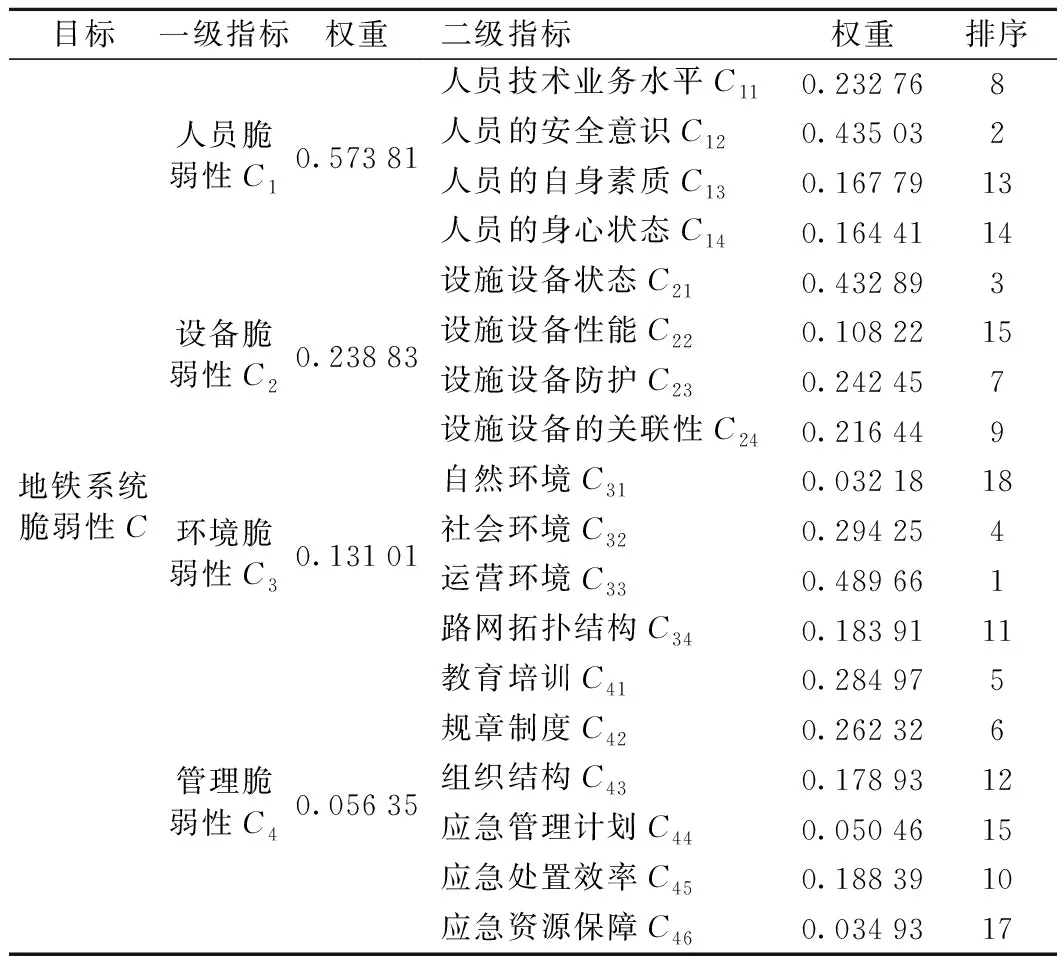
表3 地铁系统脆弱性影响因素指标权重值
3 地铁系统脆弱性仿真模型分析
系统动力学(Systems Dynamics,SD)是美国麻省理工学院(MIT)J.W.弗雷斯特(J.W.Forrester)教授最早提出的一种对社会经济问题进行系统分析的方法论和定性与定量相结合的分析方法[17]。在构建地铁系统脆弱性影响因素体系ANP结构模型,分析体系中各因素内在关系之后,利用系统动力学仿真平台Vensim_PLE软件[18],对地铁系统脆弱性进行仿真模型分析。
3.1 SD流图的构建
地铁系统是一个由多个子系统相互作用形成的整体,根据图2可知,地铁系统脆弱性分为人员脆弱性、设备脆弱性、环境脆弱性和管理脆弱性4个子系统,分析各因素之间内在关系,建立如图3所示的地铁系统脆弱性SD流图,系统变量包括4个水平变量,18个辅助变量,4个速率变量和9个常量。

图3 地铁系统脆弱性影响因素体系SD流图
3.2 仿真模型参数的确定
基于ANP已计算得到的地铁系统脆弱性影响因素各指标权重值(表3),建立地铁系统脆弱性SD方程如表4所示。
3.3 仿真分析
地铁系统脆弱性仿真模型取仿真周期为12个月,仿真步长为1个月。根据《企业安全生产费用提取和使用管理办法》(财企[2012]16号)规定,每年安全费用按企业年产值的2%提取,假设每年提取1260万元作为安全支出,平均每月105万元,4个子系统的投放比例按人员∶机械∶环境∶管理为3∶6∶2∶1进行安全投入管理。

表4 地铁系统脆弱性影响因素体系主要变量SD方程
注:水平变量初始值由专家打分法和加权平均法确定。
(1)初始状态下各子系统脆弱性变化分析
由图4可知,加入安全投入之后的地铁系统各子系统脆弱性随时间变化呈非线性趋势逐渐减少,有效的安全投入对地铁的安全管理有一定的促进作用。

图4 地铁系统脆弱性各子系统仿真趋势
(2)安全投入方案对比分析
安全投入与地铁系统脆弱性存在一定联系,通过调整总的安全投入,观察不同投入值对地铁系统脆弱性的影响,探究安全投入与系统脆弱性水平的反馈关系。采取増加或减少安全投入的5%与初始状态进行对比,对比3种情况下地铁系统脆弱性水平趋势,对比结果如图5和表5所示。

图5 地铁系统脆弱性安全投入变动方案仿真趋势
由图5和表5的反馈关系可知,适当增加安全投入,能够有效降低系统脆弱性,而减少投入脆弱性下降趋势放缓。同时,反映出增加安全资金对系统稳定的有效性。在进行地铁安全管理时,合理的安全资金安排,能够提高整个地铁系统的安全性。

表5 地铁系统脆弱性安全投入变动方案仿真结果
(3)各子因素变动方案对比分析
地铁系统脆弱性各影响因素权重已由ANP算出,在建立系统动力学模型之后,可以通过改变各子因素的变化量来反证权重计算是否合理。选取指标权重计算排序在前3的指标,分别为运营环境C33、人员的安全意识C12和设施设备状态C21,分别将3个指标减少0.04进行模拟,即单因素的变动,对比结果如图6和表6所示。

图6 地铁系统脆弱性单因素变动方案仿真趋势
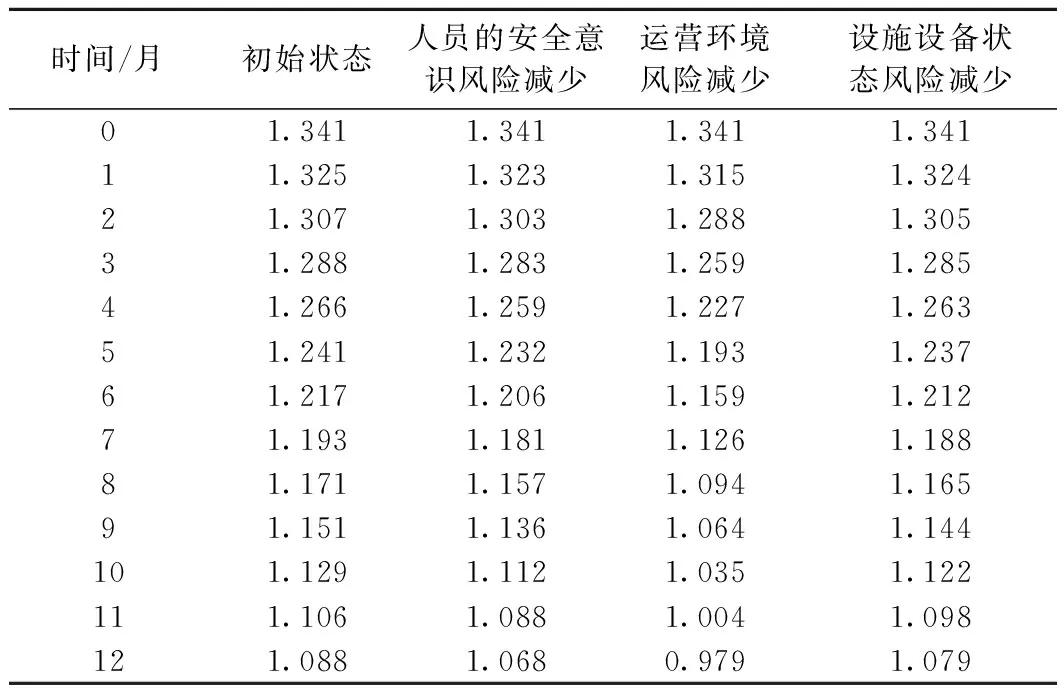
时间/月初始状态人员的安全意识风险减少运营环境风险减少设施设备状态风险减少01.3411.3411.3411.34111.3251.3231.3151.32421.3071.3031.2881.30531.2881.2831.2591.28541.2661.2591.2271.26351.2411.2321.1931.23761.2171.2061.1591.21271.1931.1811.1261.18881.1711.1571.0941.16591.1511.1361.0641.144101.1291.1121.0351.122111.1061.0881.0041.098121.0881.0680.9791.079
由图6可知,随着单个因素脆弱性的减少,地铁系统脆弱性下降趋势加快;同时可以看出,运营环境脆弱性的减少对整个地铁系统脆弱性影响最大,人员的安全意识次之,最后是设施设备状态,这与ANP计算出的权重值排序吻合,也说明用ANP理论计算具有反馈关系的系统权重值是合理且准确的。
4 结论
通过网络层次分析法(ANP)与系统动力学(SD)的结合,构建基于ANP-SD的地铁系统脆弱性仿真分析,梳理地铁系统脆弱性影响因素的同时,有效探究了安全投入以及单因素变动对地铁系统脆弱性的影响趋势。
(1)根据仿真结果可知,不同的安全投入会导致不同的系统脆弱性水平发展结果,投入与脆弱性发展水平呈非线性关系,总体而言,合理的安全投入能有效降低地铁系统脆弱性。在地铁系统管理过程中,应改善安全投入方案,加大对系统的安全投入,保证充足的资金储备,为地铁安全管理做好后备力量。
(2)ANP排序前3的影响因素分别是运营环境C33、人员的安全意识C12和设施设备状态C21,能够与系统动力学模型验证相吻合,表明ANP是适合于反馈关系系统的权重指标计算方法。对地铁系统脆弱性影响最大的3个因素,在进行地铁安全管理时,应加大对这3个影响因素的管控,保证系统的稳定,减少脆弱性的产生。
(3)地铁系统是复杂的非线性、多反馈动态系统,运用SD建立系统动力学模型,不仅能较好反映各影响因素的复杂因果关系,而且能定量反映系统在各影响因素作用下的水平发展趋势。

