轨道不平顺作用下动车组安全运行速度限值研究

张荣鹤,王 平,汪 鑫,徐井芒

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

由于地质和自然灾害的原因，线路基础结构会发生不同程度的变形，导致无砟轨道结构水平、高低及轨向的变化，产生几何不平顺。轨道不平顺和随机不平顺会恶化列车运行条件，列车以设计速度运行时，将存在较大的安全隐患，可能引起列车脱轨[1]。

当出现较大的几何尺寸偏差之后，除应进行补修、抢修之外，列车应立刻采取限速或停运的处理方式。我国《高速铁路无砟轨道线路维修规则》中对于线路轨道静态几何尺寸容许偏差管理值做出了说明，给出了200～250 km/h线路作业验收、经常保养、临时补修以及限速160 km/h等状态下的各静态几何尺寸容许偏差管理值。但基础的变形程度具有不确定性，规范中仅对限速160 km/h的各项静态偏差做出限值，当实际的几何不平顺超出此限值后，列车的限行速度将面临无规范可依的局面。因此，对于不同程度的偏差影响下，动车组安全运行速度限值的研究是十分必要的。

我国在轨道不平顺管理方面开展了大量研究工作，黄玉纯[2]运用数学方法以及计算机技术对城市轨道交通工务管理中的数据采集手段、评价方法和评价指标进行了初步的探讨。张旭久[3]通过仿真计算，从安全和舒适的角度上得到高速列车350 km/h轨道不平顺管理标准建议值。田国英等[4-6]利用轨道谱研究轨道不平顺在频域的演变规律及相应的轨道谱限值，并基于车辆-轨道耦合动力学理论，提出利用高速铁路轨道不平顺谱进行不同管理等级轨道不平顺限值估算的方法。蔡成标等[7]基于车辆-轨道耦合动力学理论，以10 m波长谐波轨道不平顺为输入激扰，进行了货车车辆运行条件下各种类型轨道不平顺的安全管理限值的仿真分析。陈果等[8-9]利用车辆-轨道耦合动力学模型，针对250 km/h速度等级的高速铁路，进行了0.01～1 m波长范围高低短波不平顺和40 m波长谐波不平顺安全管理值的分析计算。徐金辉等[10]比较了峰值管理和均值管理这两种评价轨道平顺状态的方法。全顺喜等[11]提出无砟轨道高低和方向是轨道静态平顺性控制中最重要的2个方面，并从轨道不平顺谱的角度对各种高低和方向不平顺控制方法进行分析。李明华等[12]探讨了轨道高低不平顺对列车垂向加速度的影响；通过与国内外相关标准的比较，提出在速度300 km/h时应满足的轨道最大高低不平顺幅值。杨飞等[13]分析了轨道不平顺波长对车辆动力学性能的影响，得出高速铁路长波不平顺管理波长。管震舜[14]研究了不同波长、不同幅值下轨道不平顺激扰作用对直线轨道和在曲线轨道上等多种不同工况条件下动力响应的影响。

尽管对于不平顺限值的研究已经有了一定的成果，但是针对不同限速等级的不平顺限值研究还未曾展开。因此，本次研究将以不同限速等级下的不平顺限值作为重点。

1 研究原理与方法

1.1 不平顺时域样本的获取

轨道不平顺谱是在大量轨道不平顺实测数据基础上，通过功率谱估计以及非线性曲线拟合方法得到的频率(波长)与功率谱密度间的复杂函数关系，能够用来表征某一类线路的总体几何状态。同时，轨道不平顺谱还包含了随机不平顺的各类波长成分。因此，以轨道谱反演出的随机不平顺作为输入激励，进行轨道不平顺的幅值限值的估算，不仅能反映轨道不平顺的随机特性，而且估算的限值更具有普遍性和一般性。本次研究中，采用德国低干扰不平顺谱反演随机不平顺样本作为激励。

国内外研究时，通常将轨道不平顺假设为平稳随机过程，近似服从正态分布。故可以通过3σ原理来划分不同等级的不平顺样本。在此条件下，通常认为概率小于正态分布中P(X>|μ±3σ|)=0.27%的事件为不可能事件。在反演不平顺样本时，针对某一等级的不平顺限值，应保证样本超限的概率不大于0.27%。因此，将不平顺样本的10 m弦测值拟合为正态分布后，统计其|μ±3σ|值，即为该样本所对应的不平顺限值。同时参考《高速铁路无砟轨道线路维修规则》中对轨道不平顺管理波长范围，本文反演不平顺时设定波长在1.5～42 m。

1.2 轨道几何不平顺动、静关系

通过动力学仿真计算得到的不平顺限值应为动态管理值，要得到轨道静态几何尺寸容许偏差管理值，需要利用轨道动静态几何不平顺之间的关系加以转化。在“干线轨道不平顺静态紧急补修标准和动态保养标准、作业验收标准的研究”中，建立了图1所示的轨道几何不平顺动、静关系统计曲线。曲线Ⅰ是在95%置信条件下，静态值和动态平均值的关系曲线，曲线Ⅱ为95%置信条件下，静态值和最大可能动态值的关系曲线。本次研究中，将采用曲线Ⅰ进行动、静几何不平顺的转化，最终得到动车组不同限速条件下的轨道静态几何尺寸容许偏差管理值。

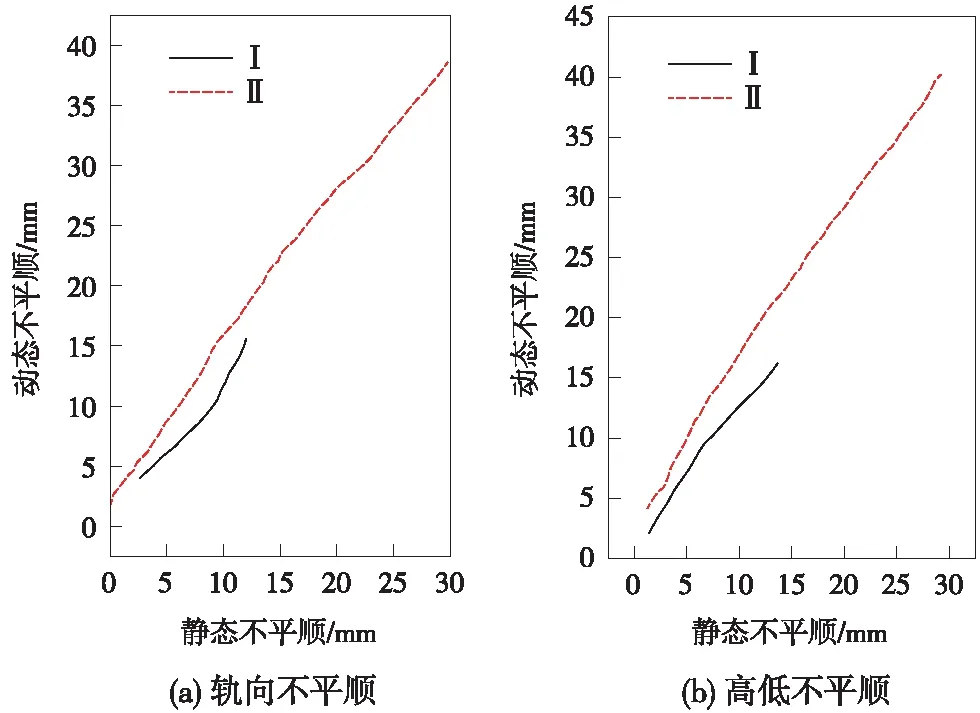
图1 轨道几何不平顺动、静关系统计曲线

1.3 研究流程

(1)利用德国低干扰不平顺谱反演随机不平顺样本。通过3σ原理，将不平顺样本的10 m弦测值拟合为正态分布后，统计其|μ±3σ|的值，即为该样本所对应的不平顺限值。

(2)对CRH2A型车和CRH5型车分别建立计算模型，施加随机不平顺样本进行计算。

(3)将计算得到的车体横向加速度、车体垂向加速度、轮重减载率、脱轨系数4个动态评价指标与规范中的限值相比较。如果没有超过限值，则换用不平顺限值更大的样本重新计算。

(4)当计算得到的动态评价指标刚刚达到或超过限值时，此时的不平顺样本的|μ±3σ|值即为当前车速下，限速至下个等级的动态不平顺限值。例如，250 km/h的车速下，轨向动态不平顺8 mm时评价指标超限，则说明列车需要限速处理。8 mm即为限速160 km/h的轨向动态不平顺限值。

(5)更换速度等级，重复进行(2)～(4)，直至得到所有速度等级下的动态不平顺限值。

(6)通过动、静态轨道不平顺关系，得到轨道几何偏差静态管理限值。

本次研究的流程如图2所示。

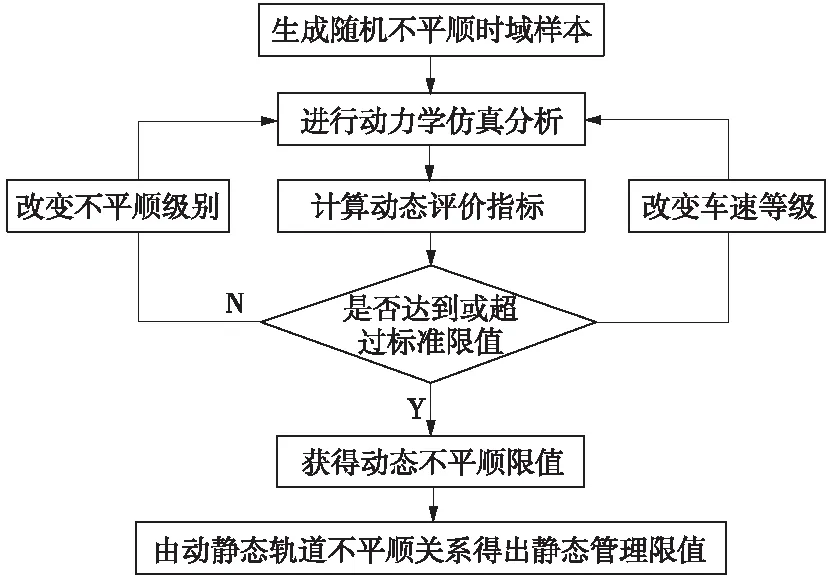
图2 研究流程

2 计算模型

为了研究无砟轨道轨向和高低不平顺对车辆-轨道耦合系统的动态影响，根据多刚体系统动力学理论，对CRH2A型车和CRH5型车分别建立计算模型(图3)，两种车型各部分结构相同，车辆基本参数有所差别。车辆系统各部分结构用等效弹簧、阻尼连接。整个车辆系统是由1个车体、2个构架、4位轮对和8个轴箱、一系悬挂和二系悬挂组成的多刚体系统。一系悬挂装置采用双拉杆轴箱定位方式，安装垂向减振器和刚弹簧;二系悬挂安装有摇枕、抗侧滚扭杆、空气弹簧系统、二系横向减振器、二系垂向减振器、横向止挡、抗蛇行减振器等[15]。钢轨采用无质量体来模拟，考虑了钢轨的真实截面形状和道岔区钢轨截面的变化，建立真实截面的钢轨模型，并将其与轨枕固结。

车辆和轨道两个子模型之间通过轮轨接触进行串联，其包括接触斑、接触法向力和接触切向力计算。通过在YOZ平面内计算轮轨接触的弹性压缩量，确定接触斑的数量、大小和位置，等效弹性接触算法将接触斑转换为与其面积及产生的轮轨接触力相吻合的等效椭圆。轮轨法向力和轮轨切向力分别使用Hertz非线性弹性接触和Kalker线性理论进行计算。

图3 计算模型

3 计算结果分析

结合实际情况，选取CRH2A型车和CRH5型车作为代表车型进行计算；限制车速不宜取得过密，也不宜取得过疏，选取250，160，120，80，40，5 km/h，共6个速度等级进行计算；对计算得到的各评价指标按99.73%置信度取值。

采用轨向和高低两类不平顺时域样本，每类样本的10 m弦测值经统计得到|μ±3σ|值，依次从4 mm取至50 mm，取值间隔为1 mm，共计94个不平顺样本。以10 mm为例，10 m弦测值的|μ±3σ|值为10 mm的轨向、高低不平顺，如图4所示。

图4 10 m弦测统计值10 mm的轨向、高低不平顺波形

本次研究中主要提取的评价指标为以下4个：车体横向加速度、车体垂向加速度、轮重减载率、脱轨系数。其中，轮重减载率和脱轨系数分别提取动车前转向架第一轮对的左右轮的计算结果。将计算结果同样按照99.73%置信度来进行统计处理，以排除极小概率的值，同时保证经济性和行车的安全性。

施加轨向动态不平顺样本时，由图5可以看出，各评价指标均随不平顺的增大而增大。其中，车体横向加速度在5 mm时超过I级标准，6 mm时超过Ⅱ级标准；车体垂向加速度在不平顺4～9 mm的范围内均未超过I级标准，且值均非常小，接近于0；轮重减载率随不平顺的增大而大幅增大，在8 mm时超限；脱轨系数在5～9 mm的范围内均未超限。

不平顺限值按照各评价指标最不利的情况确定，即轨向动态不平顺10 m弦测值为5 m m时，达到经常保养级别；为6 mm时，达到经常舒适级别；由于加速度达到Ⅲ级标准时，轨向动态不平顺10 m弦测值为8 mm轮重减载率同时超限，不再设置舒适度和临时补修级别，此时动车组以250 km/h的速度运行已不再安全，应当限速至160 km/h。

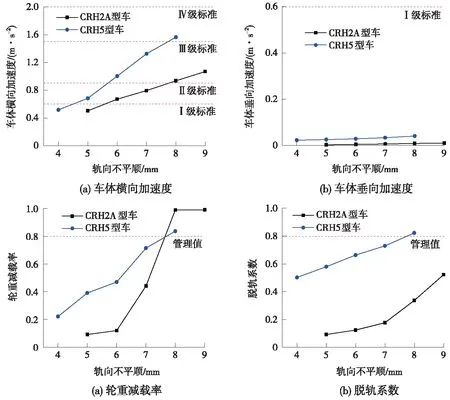
图5 250 km/h下各轨向不平顺评价指标计算结果

由图6可以看出，各评价指标均随不平顺的增大而增大。其中，车体横向加速度和脱轨系数在高低动态不平顺10 m弦测值为4～10 mm的范围内均未超限；车体垂向加速度在6 mm时超过I级标准，在8 mm时超过II级标准，在10 mm时超过III级标准，在12 mm时超过Ⅳ级标准；轮重减载率在12 mm时超过管理限值；而脱轨系数在4～12 mm范围内均未超限。

不平顺限值按照各评价指标最不利的情况确定，即高低动态不平顺10 m弦测值为6 mm时，达到经常保养级别；为8 mm时，达到舒适度级别；为10 mm时，达到临时补修级别；高低动态不平顺10 m弦测值为12 mm时，动车组以250 km/h的速度运行已不再安全，应当限速至160 km/h。

图6 250 km/h下各高低不平顺评价指标计算结果

图7 250 km/h下轨向动态不平顺8 mm时各评价指标时程

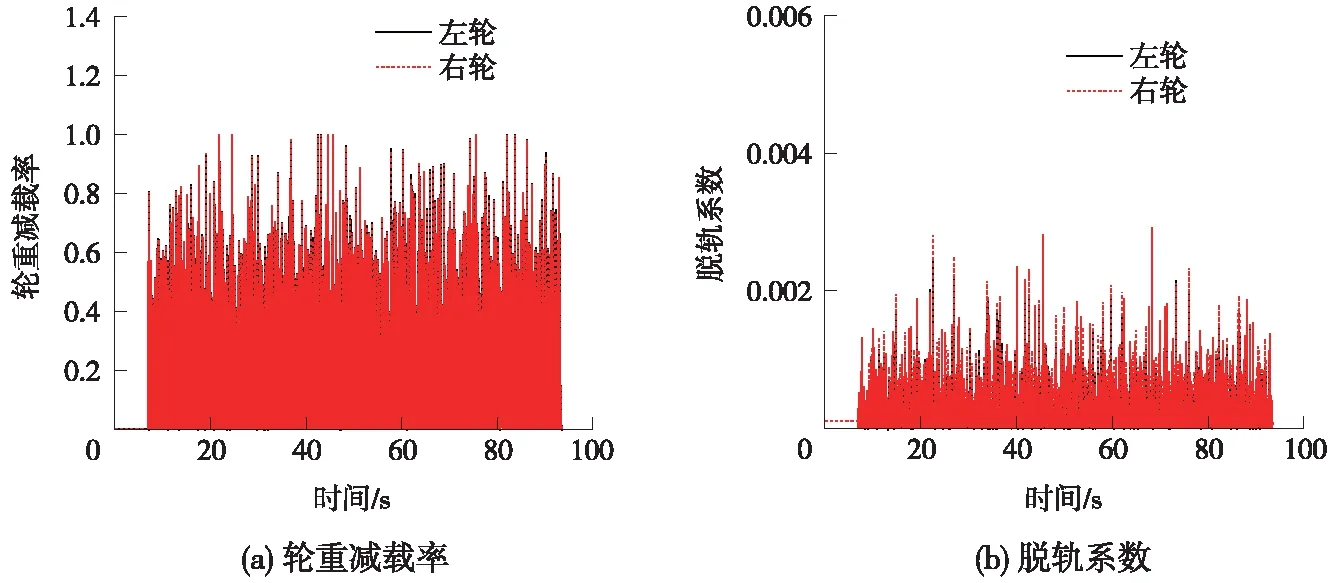
图8 250 km/h下高低动态不平顺12 mm时各评价指标时程

比较图5、图6各评价指标，在速度250 km/h时，无论是在轨向还是高低不平顺激励下，CRH5型车的各项指标大部分都比CRH2A型车的大，说明相同工况下，CRH5型车的动力响应比CRH2A型车剧烈。

提取轨向动态不平顺10 m弦测值为8 mm时和高低动态不平顺10 m弦测值为12 mm时(车速250 km/h时，超过安全限值)，各评价指标的时程曲线如图7、图8所示。可以看出，轨向动态不平顺10 m弦测值为8 mm时，对于轮重减载率和脱轨系数，轨向不平顺激励会产生较多的极大峰值；而高低动态不平顺10 m弦测值为12 mm时，轮重减载率和脱轨系数较为稳定，其中脱轨系数极大值较轨向不平顺工况下小得多。这说明，列车对于横向的激励较垂向激励更为敏感。对于横向激励源如轨向不平顺、轨距不平顺，应严格控制。

由计算可知，在速度160 km/h下，轨向和高低动态不平顺限值分别为8 mm、12 mm，低于《高速铁路无砟轨道线路维修规则》中对速度160 km/h时的容许偏差管理值10 mm、14 mm，说明计算所得限值要严于规范。当线路没有得到及时维修，随着不平顺的继续发展，限速160 km/h已经不能保证列车运行的安全，需要根据不平顺的发展程度进一步降低限制速度。

为得到进一步限速对应的不平顺值，取较大的轨向及高低动态不平顺，计算了车速160 km/h时CRH2A型车和CRH5型车在各轨向及高低不平顺下的动力响应，得到各动力学评价指标，如表1、表2所示。限速160 km/h时，随着不平顺的发展，对CRH2A型车，当轨向动态不平顺达到11 mm时，轮重减载率为0.938，高低动态不平顺达到15 mm时，轮重减载率为0.818，超过管理值0.8；对CRH5型车，当轨向动态不平顺达到10 mm时，轮重减载率为0.928，超过管理值0.8，高低动态不平顺达到15 mm时，车体垂向加速度为2.528 m·s-2，超过IV级标准。所以当轨向动态不平顺发展到10 mm，高低动态不平顺发展到15 mm时，限速160 km/h已不能保证列车的安全运行，应进一步限速至120 km/h。

结合以上分析可知，对于轨向不平顺，对限值起控制作用的是轮重减载率和脱轨系数，而车体垂向加速度始终非常小。可见，轨向不平顺几乎没有对车体造成垂向扰动；对于高低不平顺，对限值起控制作用的是车体垂向加速度和轮重减载率，而车体横向加速度和脱轨系数非常小。较小的脱轨系数是由于横向轮轨力较小。可见，高低不平顺几乎没有对车体造成横向扰动。这说明，一个方向上的不平顺只会造成同方向的扰动，对其垂直方向的扰动可以忽略不计。

表1 160 km/h CRH2A型车计算评价指标值

表2 160 km/h CRH5型车计算评价指标值

当不平顺继续发展时，需要进一步确定各轨向和高低不平顺条件下的限速标准。参考限速120 km/h时的分析方法，分别计算了两种车型各轨向和高低动态不平顺下的允许运行速度，如图9所示。轨向和高低动态不平顺值分别为14、18 mm时，应限速80 km/h；分别为19、23 mm时，应限速40 km/h；分别为30、35 mm时，应限速5 km/h。通过对比轨向和高低不平顺的计算结果，可以发现同等限速等级下，轨向不平顺的限值通常要严于高低不平顺的限值。对于两种车型的计算结果，不平顺按照最不利情况确定。

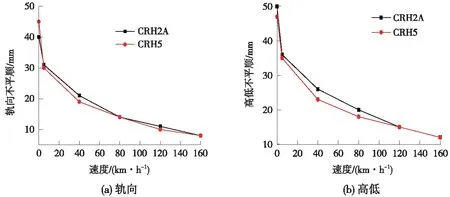
图9 各速度下不平顺限值

通过动力学仿真计算得到的不平顺限值应为动态管理值，由于在实际的不平顺测量管理时，难以准确测得动态不平顺值，因此需要利用轨道动静态几何不平顺之间的关系加以转化，得到轨道静态几何尺寸容许偏差管理值。根据图1，将计算所得各限制速度下的轨向和高低动态不平顺进行转化，得到动车各组安全运行限制速度下静态几何尺寸限值如表3所示。

表3 动车组安全运行静态几何尺寸限值

4 结论

(1)通过对比CRH2A和CRH5两种车型的计算结果，可以发现大多数工况下CRH5型车所确定的不平顺限值小于CRH2A型车。这是由于CRH2A型车的结构和参数更合理，动力学性能优于CRH5型车。

(2)对于轨向不平顺，对限值起控制作用的是轮重减载率和脱轨系数。对于高低不平顺，对限值起控制作用的是车体垂向加速度和轮重减载率。轨向不平顺主要引起车辆横向扰动，而高低不平顺主要引起车辆垂向扰动，说明方向上的不平顺激励只会对造成同方向的扰动，对其垂直方向的扰动可以忽略不计。

(3)列车对于横向的激励较垂向激励更为敏感。同等限速等级下，轨向不平顺的限值通常要严于高低不平顺的限值。对于横向激励源如轨向不平顺、轨距不平顺，应严于控制。

(4)通过动力学仿真计算，得到不同速度等级下的不平顺动态管理值，利用轨道动静态几何不平顺之间的关系转化，得到各速度等级下轨道静态几何尺寸容许偏差管理值，对现有规范内容有一定的补充。