基于EM算法的Marshall-Olkin二元指数分布的参数估计

袁守成，张 宾，陈相兵

（1.普洱学院 数学与统计学院，云南 普洱 665000；2.湖北民族学院 教育学院，湖北 恩施 445000；3.四川大学锦江学院，成都 620860）

0 引言

多元指数分布在工业技术上有重要的应用，基于不同的系统可靠性可以导出不同的多元指数分布形式。在众多形式中，Marshall-Olkin多元指数分布[1]是一类唯一保持“无记忆性”特征的分布，其中二元随机变量结构更是被广泛关注。Marshall-Olkin二元指数分布是既不被计数测度控制，又不被Lebesgue测度控制的分布[2]，并且与一元指数分布不同，Marshall-Olkin二元指数分布不属于指数族，其概率密度函数具有奇异部分，标准的参数估计方法已不再适用，需要用新的处理方法和手段对其参数进行研究。Arnold(1968)[3]用矩方法对其参数做了研究，并得到了多元指数分布参数的无偏估计；李国安(1993)[4]从二元指数分布的识别性[5]入手，利用极大似然估计(MLE)法讨论了参数的估计问题，并获得该分布参数的一致最小方差无偏估计；进一步，李国安(2015)[6]讨论了指数分布的抽样定理，并给出了四参数Marshall-Olkin二元指数分布参数的一致最小方差无偏估计。本文基于EM算法，通过引入新的潜在变量，克服了直接利用MLE确定参数的困难，给出了Marshall-Olkin二元指数分布的参数的点估计和区间估计，通过数值模拟，发现该方法切实可行。

1 预备知识

设某随机变量U服从指数分布，那么它的密度函数和生存函数可分别表示为：

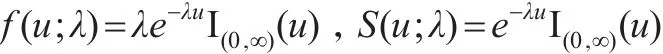
其中 Ι(0，∞)(u)表示 u 在 (0，∞)上示性函数，λ＞0 为尺度参数，记作U～E(λ)。假设三个相互独立的随机变量U1，U2，U3分 别 有 U1～E(λ1) ，U2～E(λ2) ，U3～E(λ3) ，若X1=min(U1，U3)，X2=min(U2，U3)，则二元随机向量 (X1，X2)服从参数为 λ1，λ2，λ3的Marshall-Olkin二元指数分布，记作(X1，X2)～MOBE(λ1，λ2，λ3)。

若 (X1，X2)～MOBE(λ1，λ2，λ3)，令 z=max{x1，x2} ，则它的生存函数为：

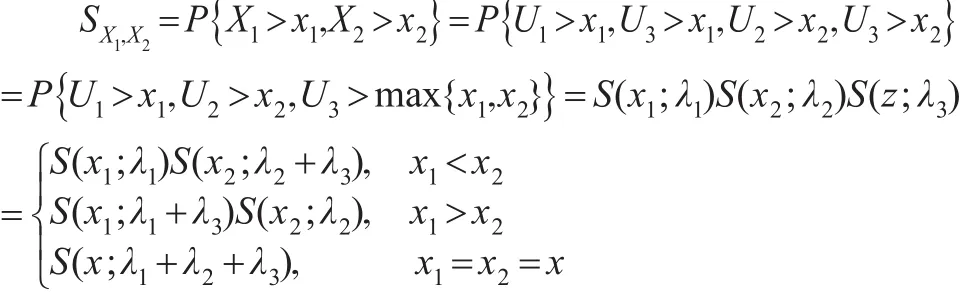
因而，X1和X2的联合概率密度为:

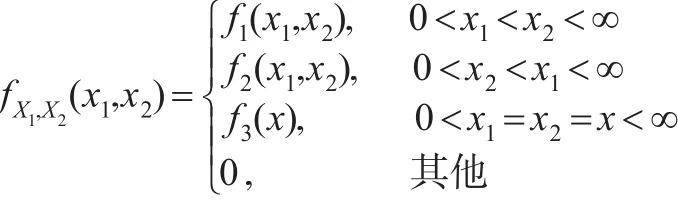
其中，f1(x1，x2)=f(x1;λ1)f(x2;λ2+λ3)，f2(x1，x2)=f(x1;λ1+λ3)

2 参数估计的EM算法

设有来自总体 MOBE(λ1，λ2，λ3)样本容量为 n 的观测值 (x11，x21)，…，(x1n，x2n)，可以做如下标记：I1={i:x1i＜x2i}，I2={i:x1i＞x2i},I3={i:x1i=x2i=x},|I1|=n1,|I2|=n2，|I3|=n3，其中 ||Ii表示集合Ii的元素个数，那么MOBE的对数似然函数可以写为：

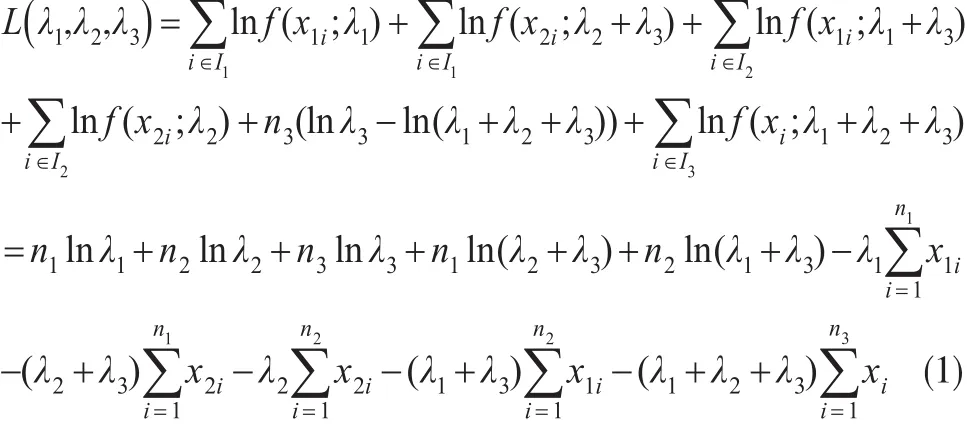
对式(1)分别关于 λ1，λ2，λ3求导，有：

容易发现,参数 λ1，λ2，λ3的 MLE 无法用显式的形式给出来,而必须要通过求解非线性方程组才能得到,这给参数的估计带来不便。下面基于EM算法对参数 λ1，λ2，λ3的MLE给予改进。

考虑到存在着一个与二元随机向量(X1，X2)相联系的潜在二元随机向量 (Δ1，Δ2),其表示为:

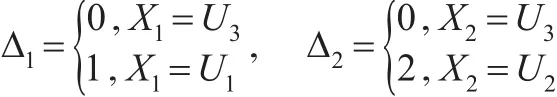
可以看到,就算 (X1，X2)已知时,(Δ1，Δ2)也未必知道。若 X1=X2,则有 Δ1=Δ2=0,这是确定的,但是如果X1≠X2,那么 (Δ1，Δ2)就不确定了。例如,当 (x1，x2)∈I1时,(Δ1，Δ2)的可能取值为 (1，0)或 (1，2)。类似地,当 (x1，x2)∈I2时,(Δ1，Δ2)的可能取值为 (0，2)或 (1，2)。

为了实现EM算法，本文采用类似于文献[7,8]中的方法。在“E步”，如果 (X1，X2)∈I3，那么 (Δ1，Δ2)是完全已知的，这时对数似然函数(1)的贡献不变；如果 (X1，X2)∈I1或(X1，X2)∈I2，把它们当做缺失数据处理。当 (x1，x2)∈I1时,(Δ1，Δ2)的可能取值为 (1，0)或 (1，2)，认为对数似然函数的贡献是由 (x1，x2，u1)和 (x1，x2，u2)两部分形成，其中 u1和 u2分别为已知 (x1，x2)∈I1时 (Δ1，Δ2)取 (1，0)和 (1，2)的条件概率，而这时的对数似然函数也被称为伪对数似然函数。类似 地 ，当 (x1，x2)∈I2时,(Δ1，Δ2) 的 可 能 取 值 为 (0，2) 或(1，2)，认为伪对数似然函数的贡献由 (x1，x2，v1)和 (x1，x2，v2)两部分形成，其中 v1和 v2分别为已知 (x1，x2)∈I2时 (Δ1，Δ2)取(0，2)和(1，2)的条件概率．在“M步”中，对伪对数似然函数关于未知参数求导，从而确定最大值。下面计算条件概率 u1，u2，v1，v2。

由于:

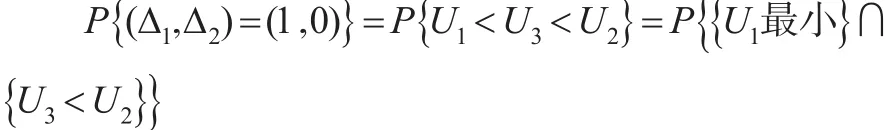
因此:

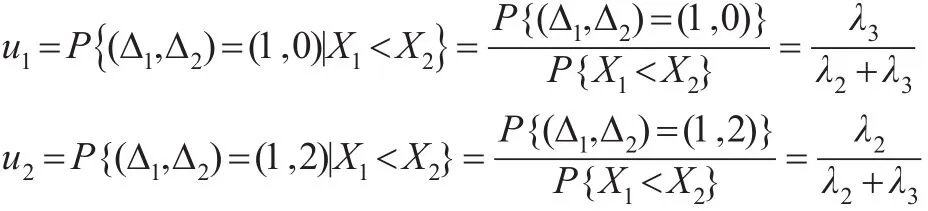
类似地，计算可得:

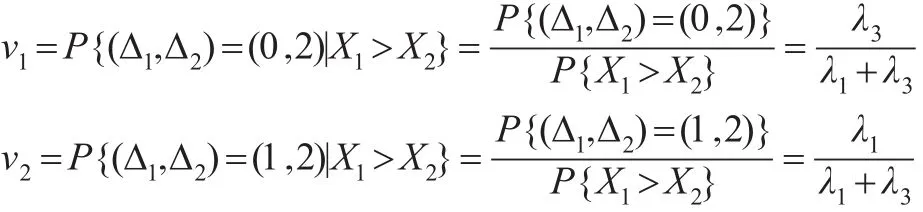
从而，伪似然函数可以写为:

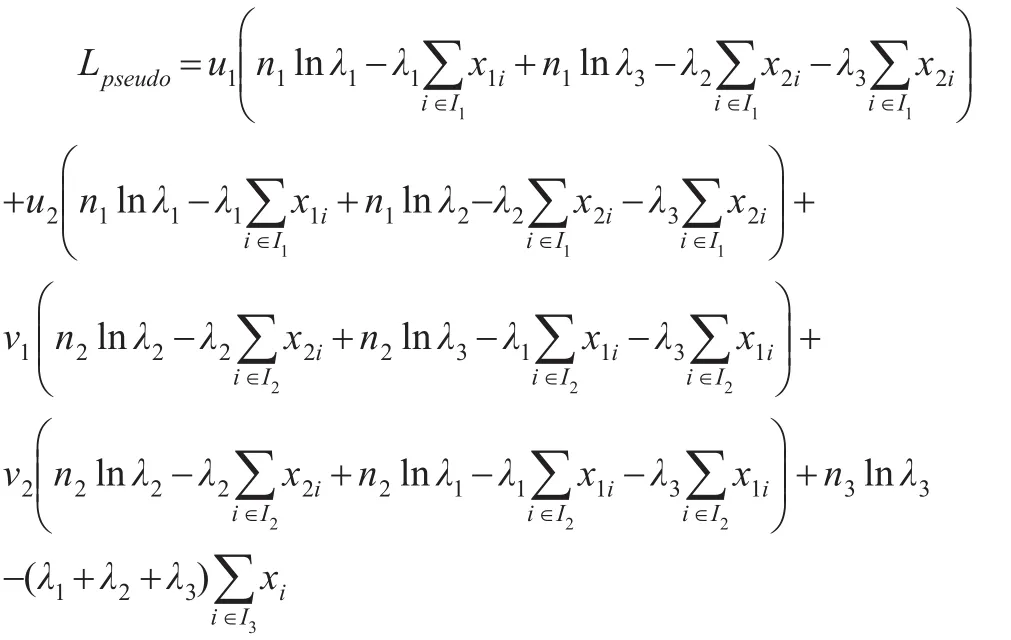
上式简写为：

在“M 步”，对式(3)极大化，分别对 λ1，λ2，λ3求导，可以得到:

下面给出EM算法的具体实施步骤：

（1）选 取 初 值 ：给 出 参 数 λ1，λ2，λ3的 初 始 估 计 值

3 区间估计

为表述方便，用V=(vij)1≤i，j≤3表示 Fisher观测信息矩阵 I-1(θ0)，则参数 λi，i=1，2，3在置信水平为1-α 下的置信区间为：

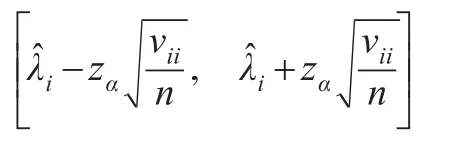
其中，zα为标准正态分布的上侧α分位点。

4 数值模拟

为了验证EM算法对MOBE分布参数估计的理论结果，本文通过数值模拟说明其估计性能。假定U1，U2，U3分布的真实参数为λ1=λ2=λ3=1，分别取样本量n＝25,50,100,150,200。由于EM算法是收敛算法，故估计的结果与初始值的取值大小无关，不妨设定初始值，并设定δ=10-5。用以下指标对EM算法的估计性能进行考察，分别为平均估计（记为AE），均方误差（记为MSE）以及置信水平为95%的区间覆盖率（记为CP），模拟次数设定为1000次。

表1 MOBE分布中参数 λ1，λ2，λ3的AE,MSE及CP

通过表1，容易发现当样本量小的时候，λ1，λ2，λ3的点估计和区间估计会有一些小偏差，但是随着样本量的增大，估计越来越接近真实值，均方误差也越来越小，同时区间覆盖率也越来越精确。从而，用EM算法给出的估计是一种相合的估计，使用该方法估计MOBE中参数是一种行之有效的方法。