学会思考，才能发现规律

◎陈秋晓

规律题是我们进入初中阶段学习的第一个难点，常作为填空或选择的压轴题.怎样才能发现规律？只要我们学会思考，全方位考虑问题，就能练就“火眼金睛”.

类型一：把图形问题转化成数字问题，探索数量变化的规律

例1 下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒……按此规律，图案⑦需_____根火柴棒.

【错解】56.

【错解原因】观察图案①，第1个图形中火柴棒有8根.在没有仔细观察后面图形数据的情况下，错以为后面每多一个多边形就多8根火柴棒，由此认为第7个图案需56根.

【正解】50.

解：根据图案①②③中火柴棒的数量可知，第1个图形中火柴棒有8根，第2个图形中火柴棒有15根，第3个图形中火柴棒有22根.这样，我们可以把图形问题转化为数字问题：序号1、2、3……对应的数依次为8、15、22……由此得出数量变化的规律：序号n对应的数应为7n+1，即第n个图案需火柴棒（7n+1）根.然后，根据题意令n=7可得答案.

【点评】如何思考，才能避免犯错？这样的图形问题，我们可以先观察图形，把它们转化为数据；然后找出每个数据与其对应序号之间的关系，得出规律；最后用具体数值代入规律，便能求出正解.

类型二：发现有序排列的数字的变化规律，作出合乎实际意义的回答

例2如图是某月的月历，竖着连续框三个数，它们的和可能是（ ）.

A.21 B.34 C.72 D.78

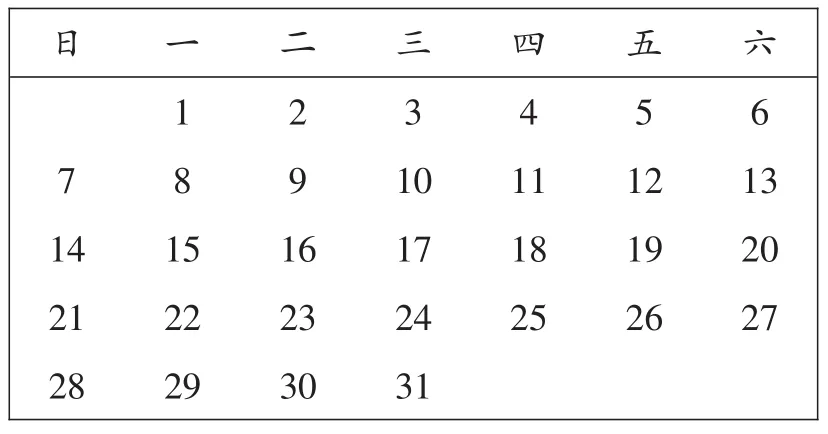
日 7 1 4一 1 8 1 5二 2 9 1 6三 3 1 0四 4 1 1五 5 1 2六 6 1 3 21 28 22 29 23 30 17 24 31 18 25 19 26 20 27

【错解】A.

【错解原因】我们在多次尝试“竖着连续框三个数”，再求其和后，不难发现数字的特殊性：和为3的倍数.于是有些同学急于求成，看到选项A即以为是答案.

【正解】C.

解：不妨设框出的三个数的中间一个为x，则它上面的数是x-7，下面的数是x+7，三个数的和是（x-7）+x+x+7=3x，故一定是3的倍数.再根据每个月的日期范围，可得x-7≥1且x+7≤31，所以8≤x≤24，24≤3x≤72.

【点评】对于此类型的题目，只要我们动手尝试，不难发现有序排列的数字的变化规律.但要注意：从生活中来，又回到生活中去.此题涉及生活中的月历，框出的三个数只能是1～31（包括1和31）之间的正整数.所以，可以由选项结果去评判是否符合实际问题的要求，也可由实际要求去求出取值范围.只有这样，才能对原问题作出合乎实际意义的正确回答.