理想河口盐度层化的减阻效应研究

杜雅静，张庆河

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

河口层化主要指水体沿垂向形成密度梯度，即密度层化。层化对水体的垂向动量和能量交换以及盐度、悬沙的垂向运输有着重要影响，因此成为潮汐河口动力学研究的重要课题。

早在1816年，Fleming[1]就在苏格兰的 Tay 河口发现盐度造成的河口水体层化，Simpson[2]等则首次分析了受淡水影响的河口海岸地区，影响水体混合和层化的四种机制。之后不断有学者对盐度层化的机理以及影响层化的因素进行了深入研究[3-5]。就密度层化对水动力的影响而言，一些研究[6-9]发现密度层化会抑制水体紊动，从而使水流运动发生变化，Herrmann和Madsen[10]通过考虑浮力效应的紊流模式研究了泥沙层化引起的垂向涡粘系数和扩散系数分布的变化，张卓等[11]比较了不同紊流模型在模拟密度分层时紊动抑制作用的差异。

实际上，层化对水体紊动的抑制作用可以体现在宏观水流运动中，那就是水流发生减阻现象，即在层化条件下，水流的摩阻与不存在密度层化时相比有所减小，水流流速有所增大[12]。Maa等提出了一维垂向模型模拟存在盐度和悬沙层化时潮流流速剖面[13]，将该模型应用于长江口中解释CS3测站出现极大落潮流速的原因[14]。目前对于盐度层化对水流摩阻特性的影响还缺乏深入研究。为此，本文将通过理想河口盐度层化模拟算例，深入分析层化的减阻效应。

1 数值模式简介

为了研究盐度层化效应，采用FVCOM三维模型对不同条件下的理想河口进行模拟。FVCOM模型是目前国内外应用较为广泛的三维水动力温盐模式，在浅水假定下采用水平非结构化网格的有限体积法求解三维N-S方程[15]。模型包括动量方程、连续性方程、温盐输运方程和状态方程，水平方向上采用Smagorinsky紊流闭合模型[16]，垂向可通过Mellor-Yamada 2.5阶紊流闭合模型封闭方程[17]。

MY2.5紊流模型包括了紊动能输运方程和紊动尺度方程

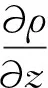
2 理想河口模型设置及验证

2.1 理想河口模型的设置

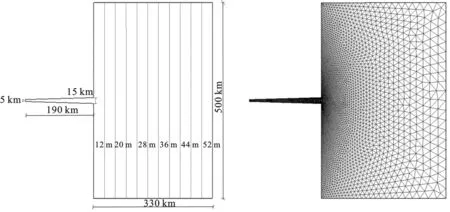
1-a 等高线差4 m 1-b 网格图图1 理想河口模型的地形Fig.1 Topography for the idealized estuary model

参照已有文献理想河口模型[4]，结合长江口地形，建立半封闭的理想河口模型，如图1～图2所示。理想河口计算域由一个喇叭形河道连接一个矩形海域组成，外海的南北东三面为开边界，其他为陆边界。河口长190 km，宽度从5 km线性过渡到15 km；外海水域长500 km，宽330 km。河道内水深8～10 m，外海水深从陆边界的8 m线性过渡到东侧海边界处的52 m。计算域采用非结构化网格，共3 979个节点，7 497个网格。河道内的分辨率为1.0 km，由河道至开边界分辨率逐渐增大，最大为25 km。垂向分层采用σ坐标，分为15层，其中在近底0.2倍水深范围内分层达到7层，可以很好地体现出近底流速变化。

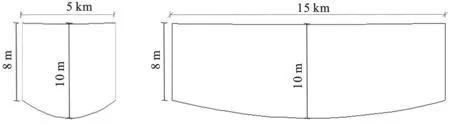
2-a 河道尽头 2-b 口门处图2 河道横剖面示意图Fig.2 Transverse section of channel

模型初始状态为静止的自由海面。本文只考虑盐度变化，不考虑温度变化，河道内初始盐度为0，口门外海域全场的初始盐度34 psu，全场温度均取为26℃。

模型由开边界的潮位和河道上游的流量驱动。河道尽头给恒定流量3 000 m3/s，入流温度均为26℃、盐度为0。开边界的潮动力取为长江口实际坐标2016年春季的M2分潮，东边界振幅0.6～0.85 m。潮动力和淡水入流使得模型趋于稳定状态。模型的科氏力取为长江口附近海域实际纬度，科氏力的存在可以生成一定沿岸流，防止口门外淡水过度聚集。底部粗糙高度设为0.001 m，符合大部分实际河口的情况[18-22]。

图3 纵向剖面和测点示意图Fig.3 Along-channel section and stations

已有研究表明，k-kl(M-Y 2.5),k-ε和k-ω等不同紊流模式在水动力、盐度上的计算结果差别不大[23-24]，因此本文的垂向紊流模型采用M-Y2.5模型。

综合稳定性和计算时长两个因素，本文将算例的模拟时间设定为75 d，此时流场和盐度场已经达到稳定状态。

2.2 理想河口模型计算结果

为了获得盐度分布情况，选取沿河道中线剖面(图3)进行分析。图4显示了该断面最后75 d最后5个潮周期平均的盐度分布。盐度为0的等值线大约入侵至口门上游30 km处，盐度为2的等值线入侵至口门上游约22 km处。在口门附近存在着明显的向陆倾斜的盐度锋面，下层盐度比上层盐度大，出现盐度层化。

为了定量判断该河口的层化程度，借鉴Hansen与Rattray[25]研究河口盐度平衡关系时采用的层化参数R，该参数也被沈焕庭等[26]选为评价混合强弱的指标，用于长江口盐水混合与层化的研究，其定义式为

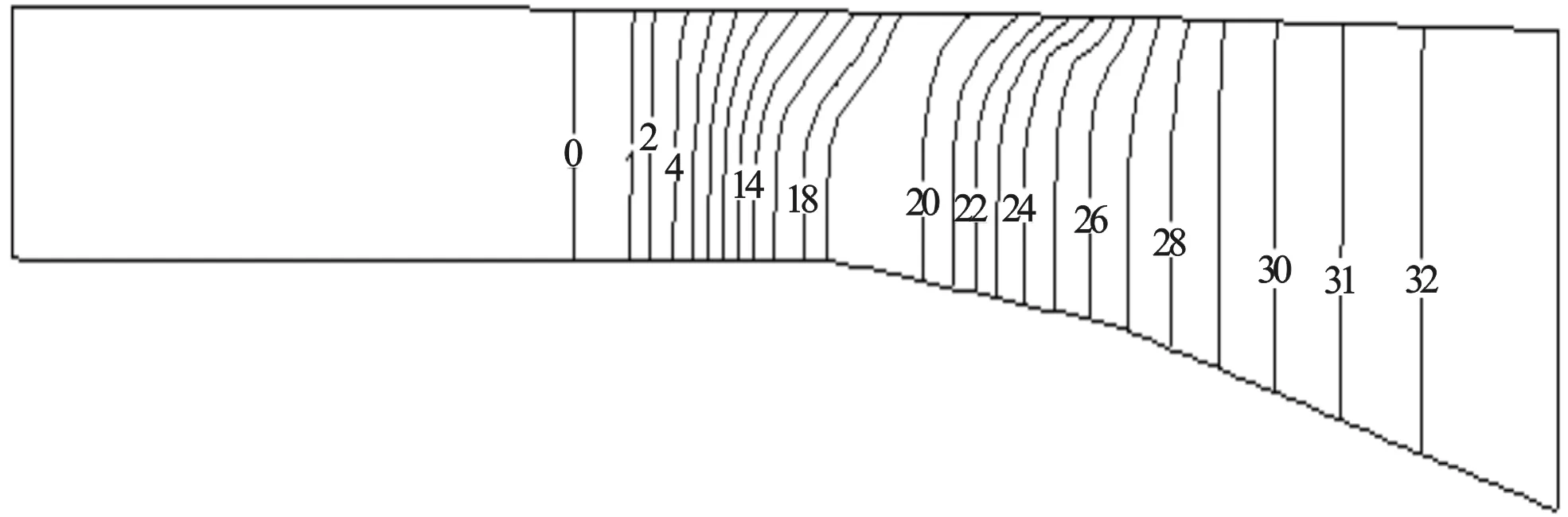
图4 断面1盐度分布Fig.4 Distribution of salinity of section 1

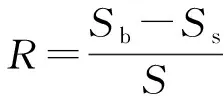
式中：Sb为某时刻测站的底层盐度，Ss为表层盐度，S为当时的垂线平均盐度。R越大，说明层化程度越好，混合越不均匀：当0≤R<0.2时，垂向混合均匀，视作垂向均匀混合；当0.2≤R<0.7时，视作部分混合型；当R≥0.7时，视作高度分层混合型[26]。

图5 沿程各点的潮平均层化参数Fig.5 Tidal-averaged stratification parameter of stations along channel

图5表现了中线断面上的潮平均层化参数。由图可知层化参数在河道内距口门10 km处达到最大，向两侧逐渐递减。根据上述判定方法，该河口在口门至口门上游20 km之间属于部分层化类型，在其他区域属于完全混合类型。

3 盐度层化的减阻效应研究

3.1 盐度层化对摩阻特性的影响

将本文第二节中的计算设置记为算例A。在此基础上，设置一组对照计算：关闭盐度开关，模型中盐度不再随着时间变化而变化，水体密度、水动力等皆不受盐度层化的影响，记为算例B。两组算例的其他变量保持一致。

摩阻流速及粗糙长度是两个重要的物理量，在物理内涵上反映了水流的摩阻特性。这两个值可通过流速剖面返求出来。但许多研究[27]表明，潮流近底流速剖面偏离传统的对数分布。虽然偏离值可能不大，但利用对数剖面去计算河底粗糙长度和剪切应力时会引起较大的误差。本文采用郝嘉陵等[28]提出的对数线性扩展模式。该模式是对传统对数分布的一种改进，在各层数据上都与实测数据具有更好的相关性，且物理量z0与u*之间具有更好的一致性和相关性，可应用于河口海岸流速分析研究。

分别求取算例A、B在一个潮周期内不同时刻的摩阻流速和等效粗糙高度，通过对比A、B计算底摩阻特性差异，可得出盐度层化对摩阻的影响。选取河道中线断面上的测点，如图3所示，其中O点位于口门处，E点位于整个入侵长度的一半处。表1和表2分别是O点和E点在算例A和算例B中摩阻特性的对比情况。

整体来看，算例A所得粗糙长度和摩阻流速都小于算例B。其中对于O点， A的摩阻流速比B小27%～52%， A的粗糙长度比B小80%左右；对于E点，A的摩阻流速比B小24%～59%， A的等效粗糙高度比B小80%～90%。总体来说，较之无层化的情况，有盐度层化时水流的摩阻流速和等效粗糙高度都有较大幅度的减小，可见盐度层化对水动力有着明显的减阻作用。

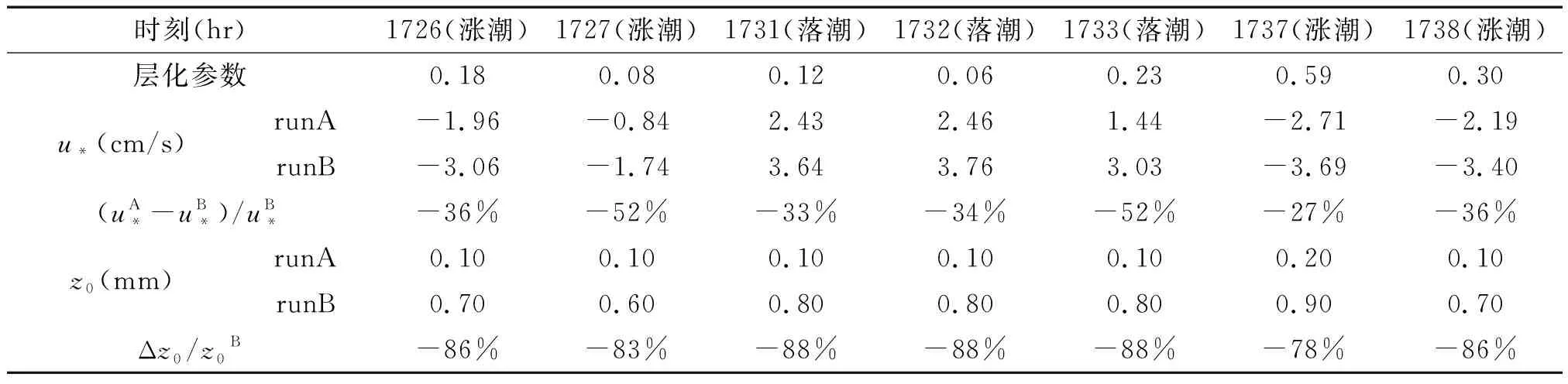
表1 算例A、B所得O点摩阻特性Tab.1 Friction characteristic of station O calculated by run A and run B

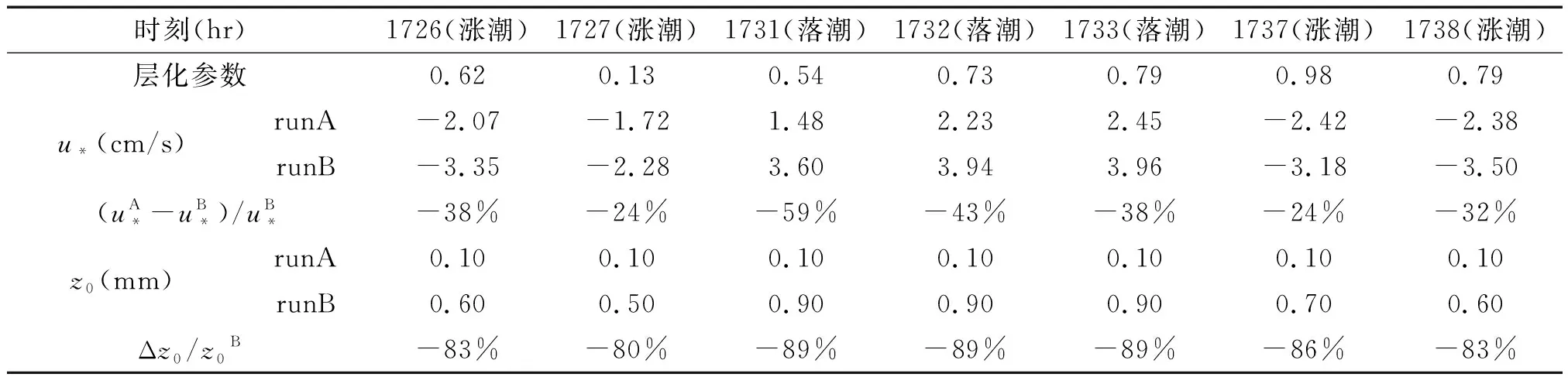
表2 E点的摩阻特性Tab.2 Friction characteristic of station E calculated by run A and run B

3.2 盐度层化减阻效应的沿程分布

图6 层化参数与减阻程度的沿程变化曲线Fig.6 Stratification parameter and drag reduction along channel图7 层化参数和摩阻流速减小幅度的关系Fig.7 Relationship between stratification parameter and (uA*-uB*)/uB*

8-a O点

8-b E点图8 O、E两点的垂向紊动粘滞系数和紊动动能Fig.8 Distribution of vertical eddy and viscosity Turbulent Kinetic Energy coefficient of station O & E

3.3 盐度层化减阻机理

层化的减阻效应实际上与盐度层化引起的垂向紊动粘性变化有关。图8是O、E两点潮平均的垂向紊动粘滞系数(KH)和紊动动能。由图可知，盐度层化使得水体各层的垂向紊动粘性系数减小，水流的垂向掺混作用减弱，紊动受到抑制故紊动动能减小，能量耗散减小，宏观上表现出摩阻特性减小的特点。这一点与孙继涛等[8]关于长江口盐度层化的研究结论是一致的。

4 结论和展望

本文建立了一个半闭合式的理想河口模型，基于FVCOM三维水动力及盐度模型模拟其水动力和盐度扩散过程。该河口盐淡水混合区域的层化参数在0.2～0.7之间，属于部分混合类型。

设置关闭盐度开关、没有层化的对比计算，引进对数扩展模式分别求取考虑盐度和不考虑盐度条件下的水流摩阻。结果表明，在一个潮周期内，考虑盐度层化条件下比不考虑盐度层化时粗糙长度减小80%～90%，摩阻流速减小24%～60%，在整体上表现为减阻。从空间分布来看，减阻程度与层化参数存在正相关关系，层化参数越大的地方，减阻效应也越明显。