n级混合微分系统第二特征值的上界不等式
卢亦平,钱椿林
(苏州市职业大学 数理部,江苏 苏州 215104)
1 主要结果
设(a, b)⊂R是一个有界区间,考虑如下n级混合微分系统
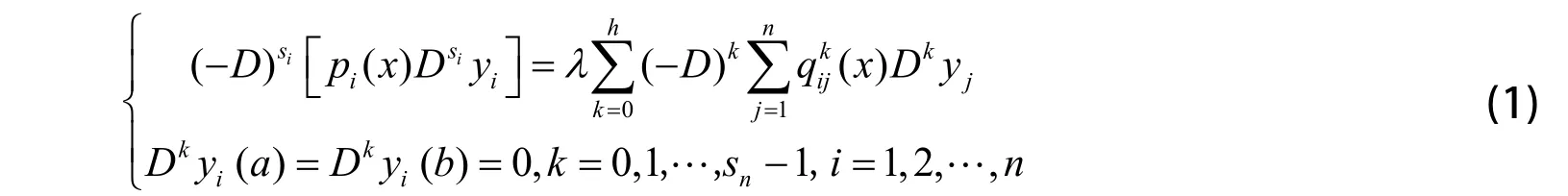

设任意的ξ=[ξ1ξ2… ξn]T,满足
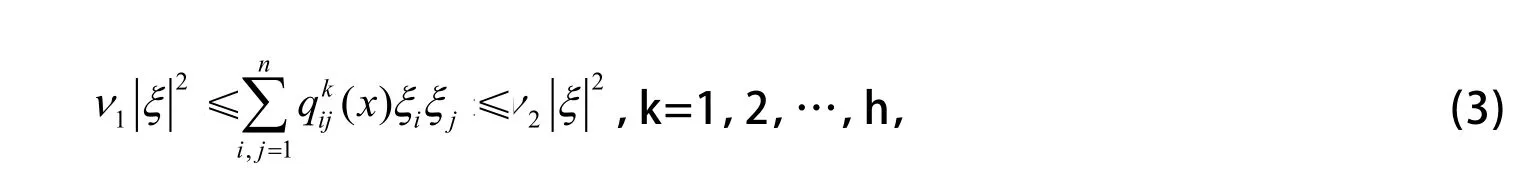
式中μ1,μ2,v1,v2为正实数。
把问题(1)写成矩阵形式,设
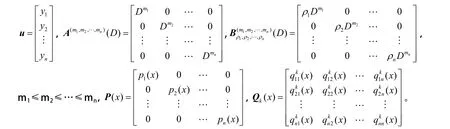
将问题(1)化为如下等价的矩阵形式

微分方程的特征值估计已有结果[1-5]。相同阶微分系统特征值估计也有结果[6]。在本文中,考虑n级混合微分系统的问题,这个问题将文献[7]的2级混合微分系统推广到n级混合微分系统的情形。运用文献[8]中的方法,对于问题(1)获得了用第一特征值来估计第二特征值的上界的不等式,其估计系数与区间的度量无关。其结果在物理学和力学中有着广泛的应用,在常微分方程的研究中起着重要的作用[9]。
定理1 设λ1,λ2是问题(1)的第一、第二特征值,且0<λ1≤λ2,σ=1,2,…,h,则有

注1 取n=2,s1=s,s2=t,p12(x)=p21(x)=0,得到文献[7]中的式(5),所以文献[7]是本文的特例。
2 定理1的证明
设λ1是问题(4)的第一特征值,相应于λ1的特征向量函数为u1,简记u=u1,且满足
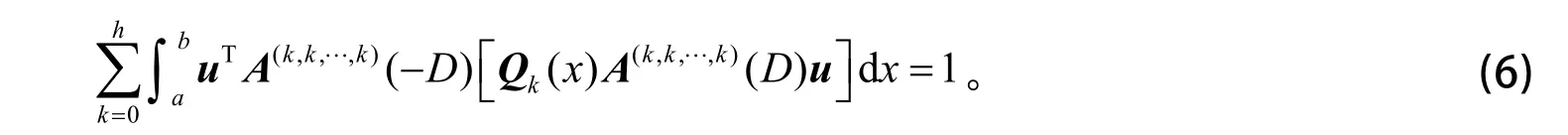
利用分部积分和式(6),得
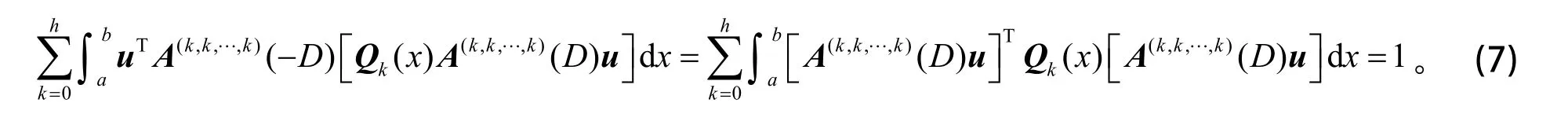
利用分部积分和式(7),有
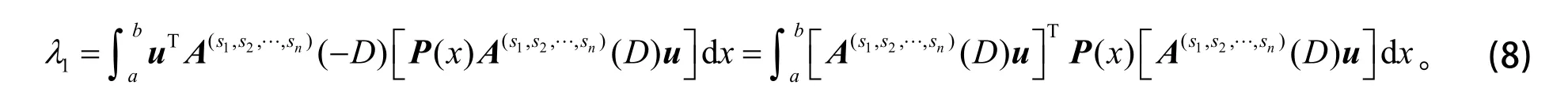
利用式(2)和式(8),得

利用式(9),有

利用式(3)和式(7),得
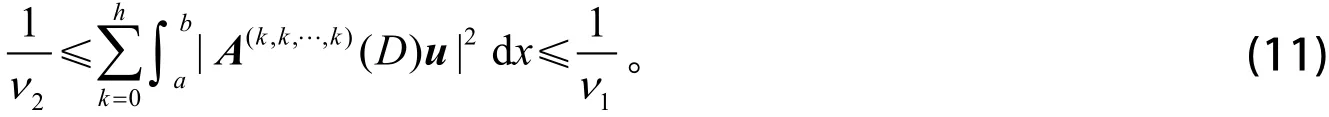
利用式(11),有
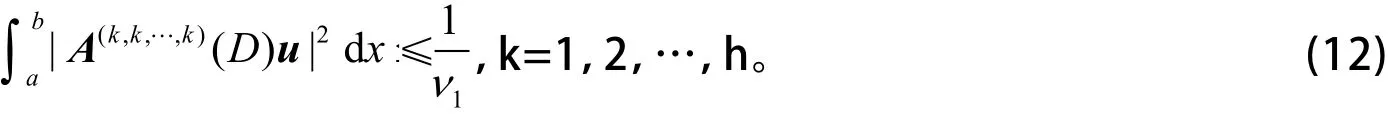
利用式(12),得

设 ϕ (x) = (x −g)u ,其中
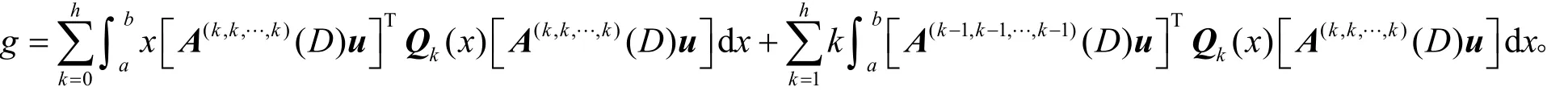
利用分部积分,直接计算得
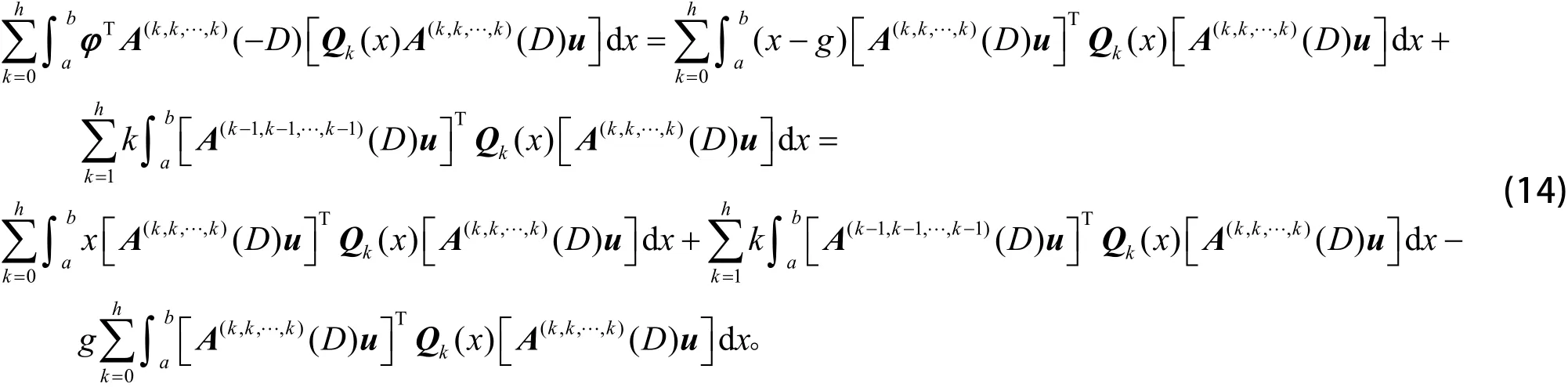
利用式(15)知,φ与u广义正交,且满足φ(k)(a)=φ(k)(b)=0,k=0,1,…,sn-1。
利用Rayleigh定理,则有
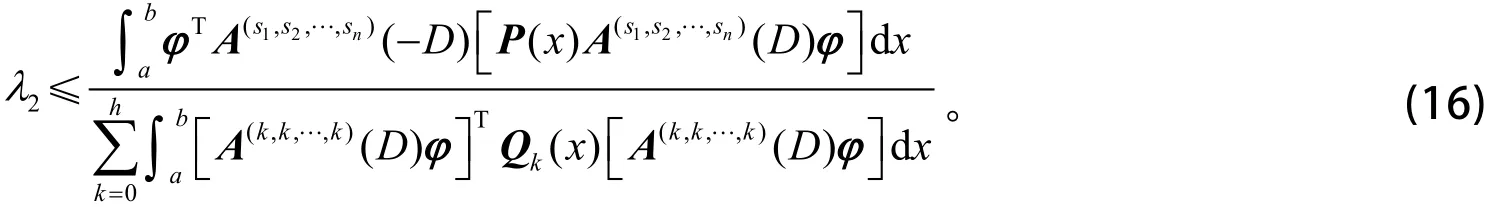
计算得
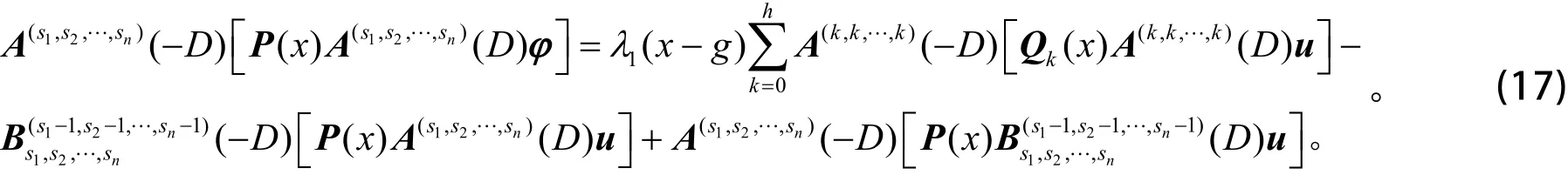
利用分部积分和 ϕ (x) = (x −g)u ,有
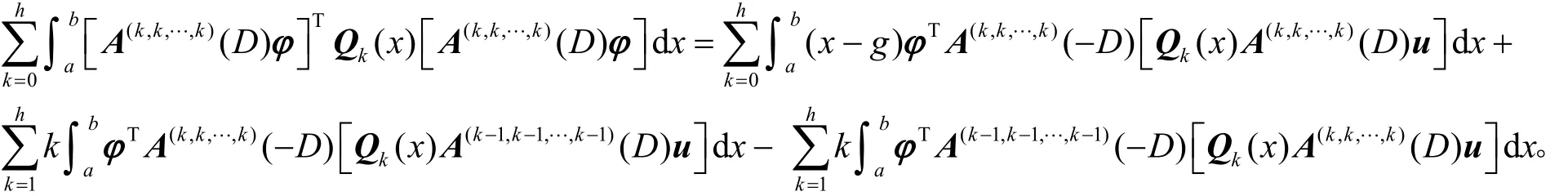
从而有
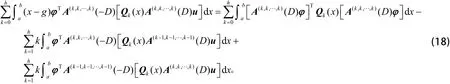
结合式(17)和式(18),得
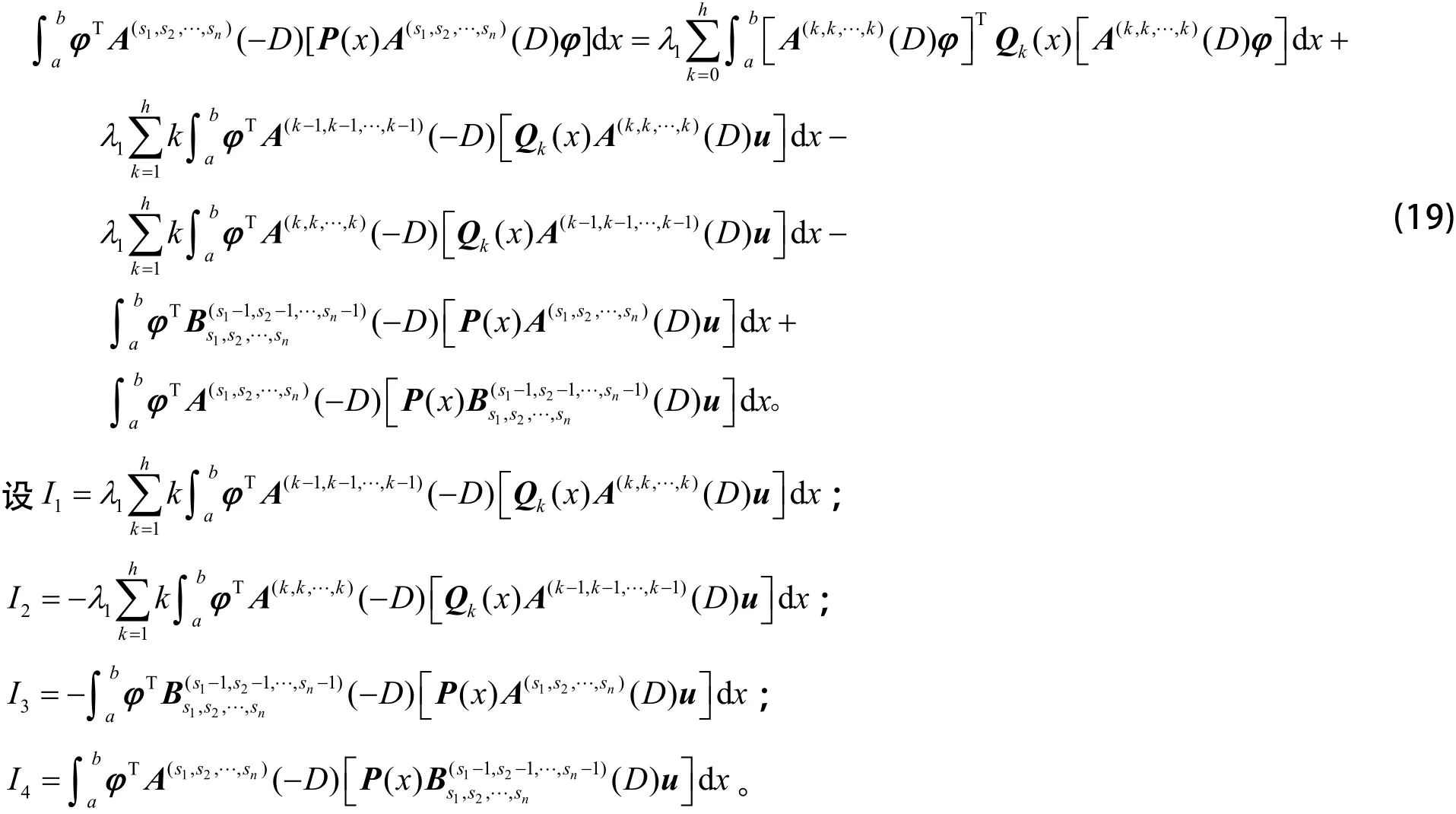
利用式(19),有
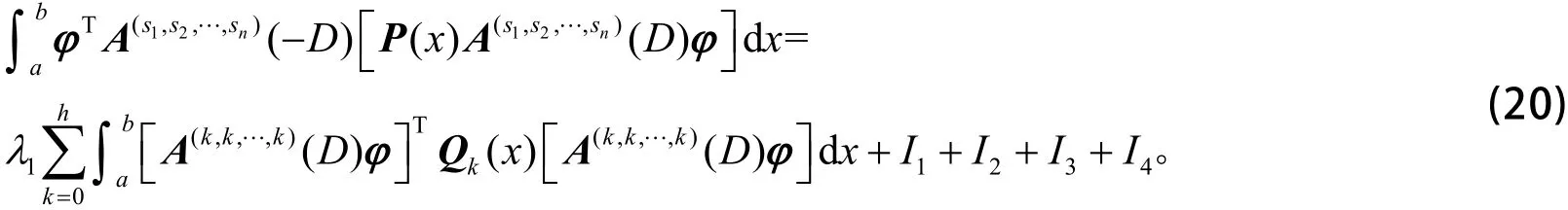
利用式(16)和式(20),则有
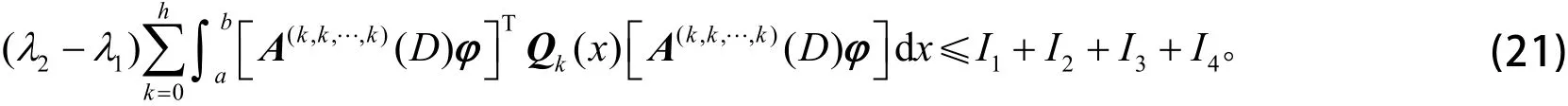
引理1 设y是问题(4)所对应第一特征值λ1的特征向量函数u的某一分量,σ=1,2,…,n,i=1,2,…,n,则
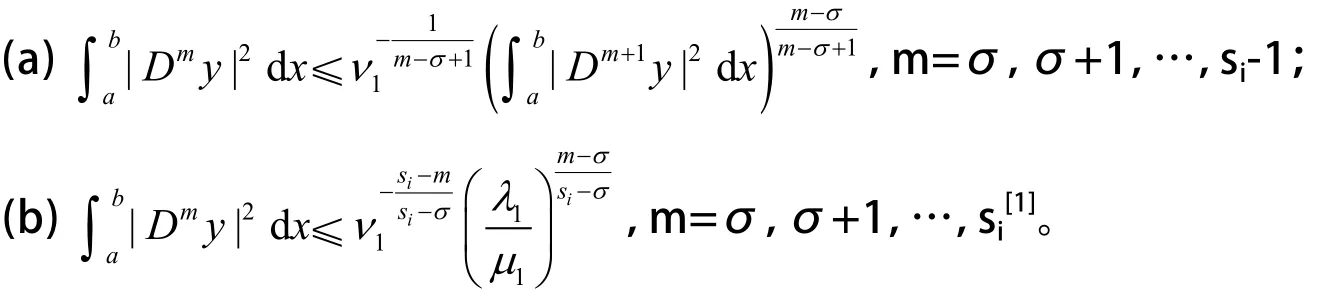
引理2 设λ1是问题(4)的第一特征值,则
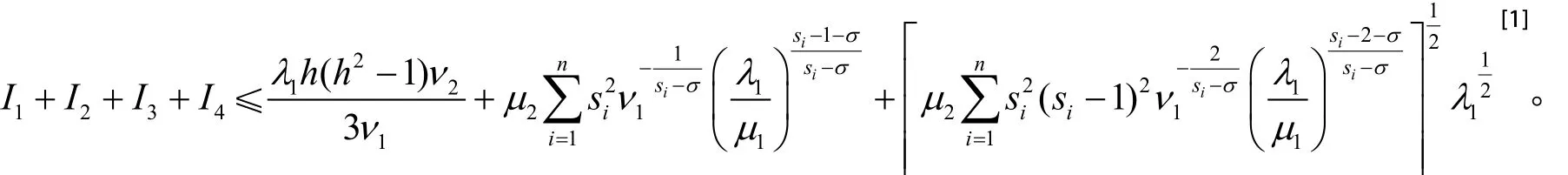
引理3 对于φ与λ1,有不等式成立

证明 利用分部积分和 ϕ (x) = (x −g)u ,得
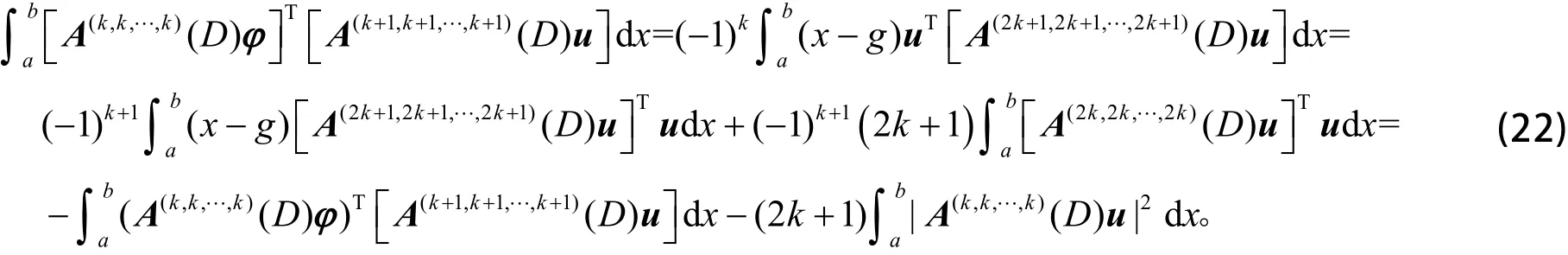
利用式(22),有
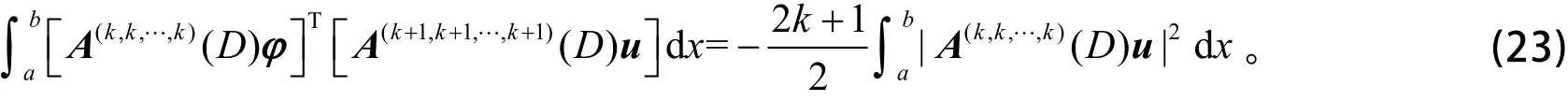
利用式(23),得
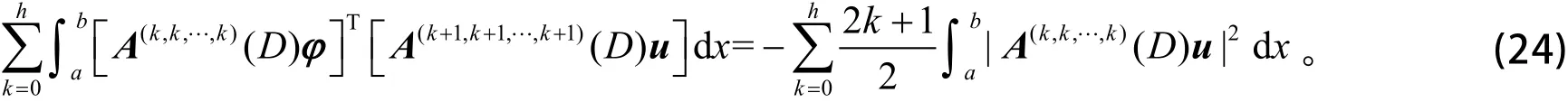
利用式(3)和式(11),得
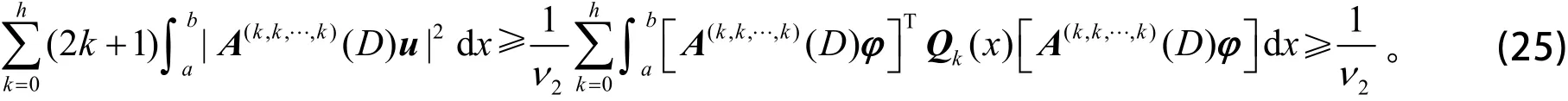
利用式(24)、式(25)、式(3)、式(11)、引理1(b)和Schwarz 不等式,得
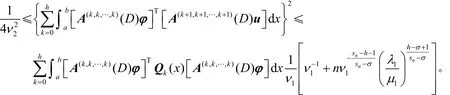
整理上式,可得引理3.
定理1的证明 利用引理2、引理3和式(21),得到定理1的式(5).
3 结论
本文利用试验函数、分部积分和不等式等估计方法与技巧,考虑n级混合微分系统第二特征值的上界估计,获得了用第一特征值来估计第二特征值的上界的不等式,其估计系数与区间的度量无关。其结果在常微分方程的研究和应用中起着重要的作用。

