潜变量增长混合模型在医学研究中的应用*

喻嘉宏 陈小娜 郜艳晖 张岩波 陈柏楠 孔羡怡 杨 朔 李丽霞△

【提 要】 目的 介绍潜变量混合增长模型理论，并将该模型应用于医学研究实践。方法 以453名接受治疗的抑郁患者的随访研究为例，采用Mplus7.4软件构建潜变量混合增长模型。结果 识别出2个增长趋势不同的亚类“一般抑郁组”和“严重抑郁组”，每个亚类人数分别为380人(83.89%)和73人(16.11%)，年龄较小患者属于“一般抑郁组”可能性高(t=-0.051，P<0.05)。结论 潜变量增长混合模型在纵向数据分析中能够识别不可观测亚群的不同增长轨迹，可以很好的弥补传统的增长模型在探讨群体异质性方面的不足，是纵向数据分析的有力工具。

随着大数据时代的到来，医学、心理学、社会学等领域的大型人群队列研究越来越多，队列研究中的数据是对每一个个体在不同时间点多次重复测量得到的追踪数据，即纵向数据。纵向数据中同一个体的多次重复观测之间往往具有相关性，不同时间点的观测变量取值不独立[1]，如何处理这种个体内的相关性便成为纵向数据分析中必须要解决的问题。目前，纵向随访数据常用的分析方法有时间序列分析(time series analysis，TSA)、多水平模型(multilevel modeling，MLM)、广义估计方程(generalized estimated equation，GEE)和潜变量增长曲线模型(latent growth curve modeling，LGCM)等，这些方法可以对所研究特征的总体发展趋势进行分析，或者探讨个体的特征随时间变化的特点以及个体间发展变化趋势是否存在差异。但不论哪种分析方法前提都假设全部研究对象的发展趋势是相同的。越来越多的研究显示研究总体中可能存在不可观测的亚群[2]，不同亚群拥有各自不同的增长参数，即不同的增长轨迹，传统的纵向数据分析方法无法识别潜在亚群，这可能会导致研究结果的准确性和预测效果降低[3]。

Muthen等人[4]1999年提出潜变量增长混合模型(latent growth mixture modeling，LGMM)，该模型是识别纵向数据变化趋势的新的纵向数据分析方法。当研究的全部个体的发展趋势不一致时，LGMM可以很好的弥补传统的增长模型在探讨群体异质性方面的不足。LGMM假设总体中存在多个潜在的增长轨迹，每个潜在的轨迹代表一个亚类，不同亚类的增长模式不同，即允许研究总体存在异质性。该模型的运用能够对预防、临床治疗及病因探索等研究领域提供研究线索。本文介绍潜变量增长混合模型的基本原理，并通过实例来介绍该方法的实际应用。

方法介绍

1.模型的概念

潜变量增长混合模型将研究总体分成若干个不可观测的亚群，并描述亚群的发展轨迹和亚群内个体随时间变化的情况，该模型包含两种潜变量：连续潜变量和分类潜变量。连续潜变量包含增长特征参数截距和斜率，分类潜变量把研究总体分成互斥的亚群来描述群体的异质性[5]。

潜变量增长混合模型的表达式如下：

(1)

(2)

(3)

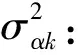
模型中也可以考虑协变量X对发展轨迹的影响，图1是包含协变量的LGMM路径图，图中有五次重复测量(Y1，Y2，Y3，Y4和Y5)，分类潜变量C和连续潜变量(截距α和斜率β)。Li等人[7]研究发现协变量在确定模型潜在的类别个数上有重要的作用，故协变量的纳入能够提高模型识别不可观测亚群的能力。

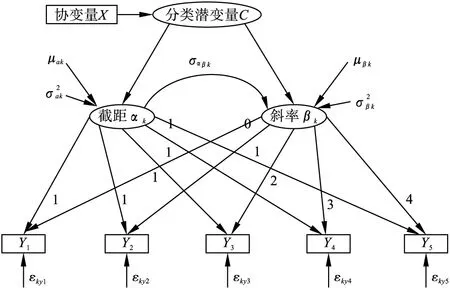
图1 包含协变量的LGMM模型路径图

2.模型参数估计

潜变量增长混合模型的参数估计方法常用的有最大似然法(maximum likelihood，ML)和贝叶斯法，这两种方法均是对数据进行多次迭代，获得模型参数的估计值和后验概率。目前，潜变量增长混合模型常在Mplus或Amos中拟合，两种统计软件进行参数估计时分别采用最大期望算法(expectation-maximization，EM)和马尔科夫链蒙特卡洛法(markov chain monte carlo，MCMC)。当研究数据存在缺失值时，Mplus 7.4软件会采用完全信息极大似然估计法(full information maximum likelihood estimator)对模型进行拟合[8]。

3.模型类别数的确定

确定LGMM模型的类别数是模型拟合的关键，一般根据信息指数与模型拟合检验结果来选择模型类别个数。常用的信息指数有AIC，BIC和aBIC指标，Karen等人[9]研究指出aBIC是最好的信息指标，该指标越小说明模型的拟合效果越好。此外，Entropy值表示模型能够将个体归为相应类别的精确程度，取值在0～1之间，一般大于0.80可认为该模型的分类准确性较高[10]。常用的模型拟合检验有BLRT检验(bootstrapped likelihood ratio test)和VLRT检验(vuong-lo-mcndell-rubin likelihood ratio test)，其中BLRT检验比较含C类的模型与C-1类模型拟合情况，若结果P<0.05，则提示含C个亚类的模型更优；反之，则C-1类模型拟合较优。VLRT检验也能够评价C类模型与C-1类模型拟合情况，VLRT检验在确定类别数目时比BLRT检验更为敏感，故VLRT检验结果更加可靠。Tofight等人[11]研究认为aBIC和VLRT检验是正确选择模型类别数的两个最佳指标。

实例分析

1.资料来源

研究对象为山西医科大学附属医院收集的符合DSM-Ⅳ(《诊断与统计手册：精神障碍》)抑郁发作诊断的患者。纳入标准为年龄在18～65岁，首次测量汉密顿抑郁量表(hamilton depression rating scale,HAMD)总分≥7分且整个随访调查中缺失次数<3次的患者。本研究共有453名患者满足入选标准。

2.研究方法

每名患者接受抑郁治疗后，每隔3周采用HAMD量表测量患者的抑郁状况，该量表包含17个项目，共5个维度，大部分条目采用5级评分法，“0～4”分别表示无、轻度、中度、重度、很重；少数条目采用3级评分法，“0～2”分别为无、轻中度、重度，量表得分越高表明抑郁情况越严重[12]。本研究仅采用前5次的得分数据，并记录患者的年龄、性别等人口学特征指标。研究探讨患者抑郁症状随时间的改善情况，将人口学特征指标作为协变量，5次重复测量的抑郁得分作为可测变量分别拟合线性、二次、自由估计三种类型增长混合模型。使用Epidata 3.1软件进行录入，使用SAS 9.4对人口学变量进行统计描述，Mplus 7.4软件进行潜变量混合增长模型分析。

3.结果

纳入研究的抑郁症患者共453人，年龄为(32.49±11.78)岁。其中男性217人，占47.90%；女性236人，占52.10%。其他人口学特征指标见表1。

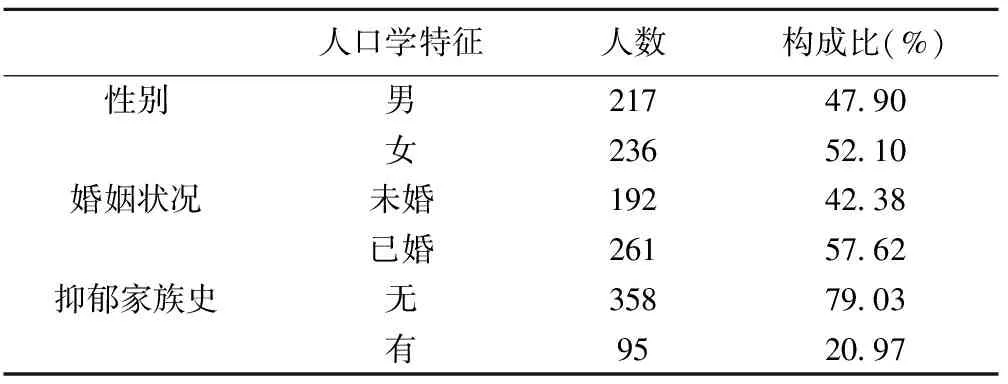
表1 抑郁症患者人口学特征

将潜在类别数从1增加到3，分别拟合线性、二次、自由估计三种类型增长混合模型，结果见表2。除含3个潜类别自由估计的LGMM外，BLRT均大于0.05，且VLRT在3个潜类别时也大于0.05，自由估计时Entropy值最大(Entropy=0.812)，结合信息指标提示含2个潜在类别自由估计的LGMM模型较优。

采用自由估计的含2个潜类别的模型参数估计结果和增长趋势图分别见表3和图2。第一类截距和斜率的均值分别为18.935(P<0.05)和-6.607(P<0.05)，该类起始抑郁得分较低，随时间变化下降速率先加快后减缓，命名为“一般抑郁组”，该组380人，占83.89%。第一类截距和斜率的方差分别为16.187(P<0.05)和3.247(P<0.05)，说明该类个体间抑郁水平初始值和抑郁下降率均存在差异。第二类截距和斜率的均值分别为23.081(P<0.05)和-1.814(P<0.05)，该类起始抑郁得分较高，处于严重的抑郁水平，随时间变化下降速率先缓慢后加快，命名为“重度抑郁组”，该组73人，占16.11%。第二类截距和斜率的方差为18.847(P<0.05)和1.415(P=0.072)，说明该类个体间抑郁水平初始值存在差异，而抑郁下降率差异没有统计学意义。第一类与第二类的截距与斜率间的协方差分别为-6.025(P<0.05)和-3.939(P<0.05)，说明抑郁水平初始值与抑郁下降率之间存在关联，抑郁水平初始值越高，抑郁下降率越小。

表2 增长混合模型拟合统计量结果

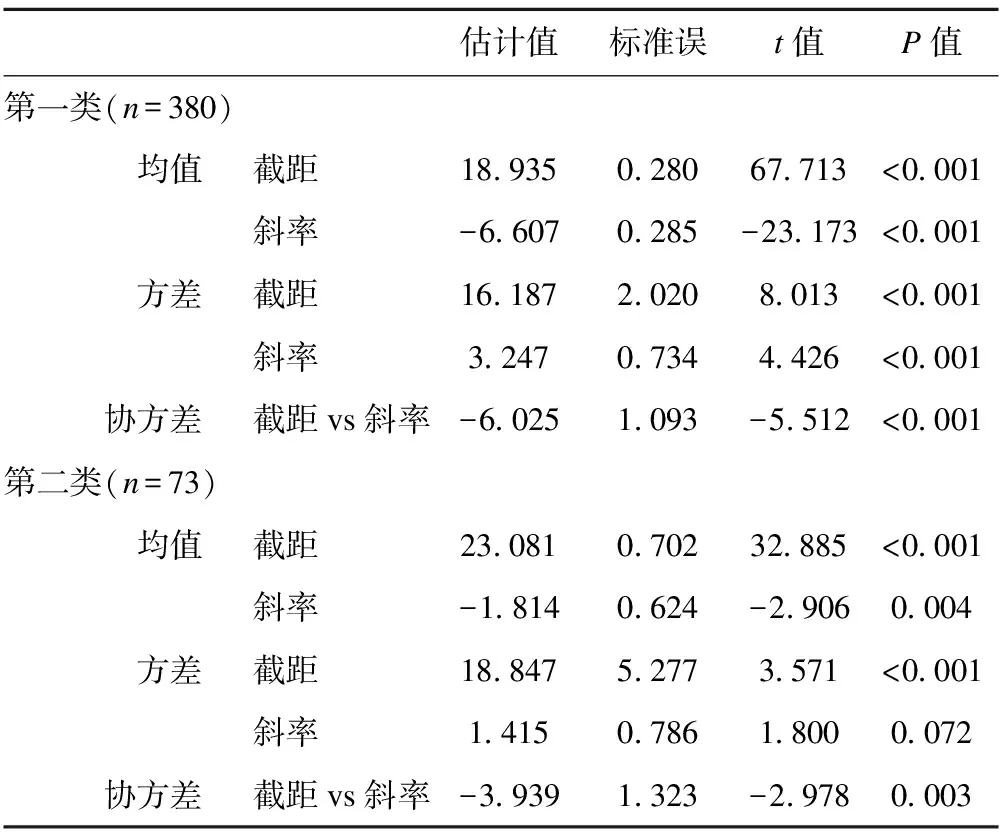
表3 抑郁症发展趋势的两个类别模型参数估计结果

以亚类为因变量(以第二类为参照)，人口学特征指标为自变量拟合logistic回归，结果见表4，结果显示仅年龄有统计学意义，其估计值为-0.051(P<0.05)，说明年龄较小的患者，更容易分到第一类，即年轻患者出现一般抑郁的可能性大。

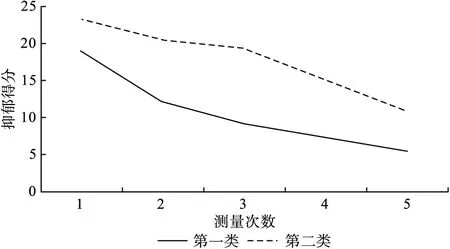
图2 两类别LGMM增长趋势图

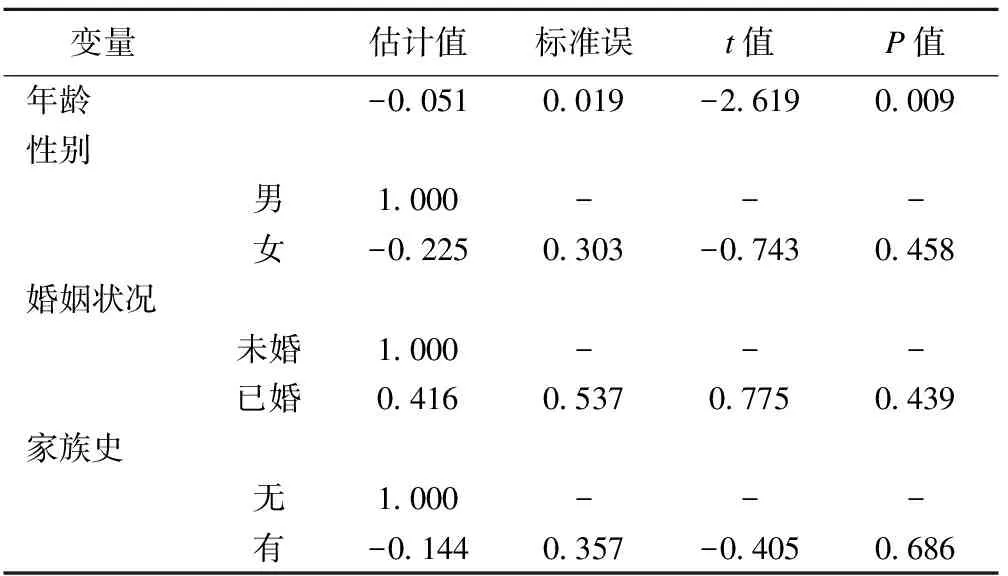
变量估计值标准误t值P值年龄-0.0510.019-2.6190.009性别男1.000---女-0.2250.303-0.7430.458婚姻状况未婚1.000---已婚0.4160.5370.7750.439家族史无1.000---有-0.1440.357-0.4050.686

讨 论

传统的纵向数据分析方法假设研究总体的增长轨迹是相同的，越来越多的纵向研究提示增长轨迹存在异质性的情况，许多研究结果已证实增长混合模型在公共卫生预防和临床疾病病因探索等研究中都能很好地识别潜在的异质性亚群，这使得增长混合模型在纵向研究领域开始受到广泛的关注。Ryan等人[13]在一项关于青少年抑郁症研究中，构建LGMM模型发现抑郁的四种发展轨迹，认为校园暴力、网络暴力和犯罪等是影响青少年抑郁发展的因素，建议学校管理者根据抑郁发展类型制定相应有针对性的预防措施进行干预。Yoo等人[14]将LGMM用于研究随访5年的慢阻肺病人生活质量变化情况，结果提示存在五种发展轨迹，发现年龄、睡眠质量、抑郁水平等因素对患者生活质量增长轨迹有影响，建议医生根据慢阻肺患者具体情况提出个性化方案提高患者生活质量。本研究采用增长混合模型对抑郁患者随时间抑郁发展情况进行分析，识别出“一般抑郁组”和“严重抑郁组”两个不同增长轨迹的潜在亚群，为疾病治疗方案的制定提供科学依据。

LGMM模型最大特点是将连续潜变量和分类潜变量结合起来，该模型通过分类潜变量将研究总体识别为不同亚群，并根据连续潜变量描述不同亚群发展趋势以及个体间是否存在差异[15]。拟合LGMM模型时潜在类别数的确定至关重要，虽然根据信息指数等指标可以提供一定的信息，但潜在类别数的选择仍存在一定的主观性，建议结合专业知识为模型的构建提供理论支持。另外，LGMM模型虽然可以分析非正态分布的变量，但数据的非正态性可能存在多种原因：有可能是真实的非正态分布，亦或是多个不同分布类别的混合[16]，故研究者可以把数据随机分成两组(训练数据集和测试数据集)或使用新一批数据进行建模来比较结果是否一致来确认类别数选择的正确性。LGMM模型需要足够的样本量，否则类别识别的准确率会降低，模型类别数的选择可以参考与样本量无关的Entropy值。

目前，LGMM模型已在多个研究领域有成功的应用，该模型在纵向数据分析中能够识别不可观测亚群的不同增长轨迹，进而深入剖析纵向数据中个体的发展情况，具有传统增长模型所不具有的优势，相信会在越来越多纵向数据分析中被采用，为相关学科研究者提供更加科学合理的建议。