横观各向同性岩体中地应力反演的参数敏感度分析

张志增，张 欣

(1.中原工学院建筑工程学院，河南 郑州 450007； 2.中建七局安装工程有限公司，河南 郑州 450053)

0 引 言

长期以来，岩土工程的随机性、复杂性以及不可预见性使岩土体材料性质和地应力参数的精准获得成为岩土工程中的一项重要研究课题[1]。岩土体参数的选取是影响工程稳定性分析结果的主要因素，对采矿工程的安全稳定有着不可估量的影响。确定岩土体参数和地应力的现场原位试验法、实验室试验和经验类比法，由于其各自存在的局限性，不能完全真实的反应出实际工程中的岩土体参数与地应力状况[2-5]。大量研究表明，基于现场量测信息的位移反分析方法为确定岩土体参数和地应力状况提供了一条新途径，在采矿工程中发挥了重要的作用[6]。

Kavanagh等在20世纪70年代为位移反分析方法奠定了理论基础[7]。经过40多年的发展，位移反分析方法的研究在国内外已经取得了丰硕的成果[8]。研究涉及弹性问题、黏弹性问题、弹塑性问题和横观各向同性问题[9-13]。原位地应力作为岩土工程中的重要参数，一直是国内外学者研究的重要对象。已有地应力反分析文献中，多为对反分析计算方法的优化理论，对地应力反分析的稳定性研究鲜有报道。张志增等[14]推导了横观各向同性岩体中深埋圆形巷道的位移解析解，并对位移反分析的唯一性进行了分析[15]。本文将在上述研究的基础上，对横观各向同性岩体中地应力反演的参数敏感度进行分析。

1 计算模型的基本假定

建立如图1所示的坐标系，假定xoy面为横观各向同性面，oz为对称轴。

图1 横观各向同性材料示意图

横观各向同性岩体中深埋圆形巷道模型见图2，其基本假设如下：①巷道围岩为横观各向同性弹性体，开挖后位移和应变均为微小；②巷道走向垂直于横观各向同性面；③模型为平面应变问题；④巷道为埋深巷道， 忽略巷道上部和下部的初始应力差[16]；

⑤竖直方向地应力为p，水平地应力为q；⑥忽略影响范围内的自重。

图2 深埋圆形巷道模型图

2 地应力反演模型的敏感度分析

2.1 横观各向同性岩体中深埋圆形巷道地应力反分析数值模型

根据巷道模型的假设和描述，张志增等求得了横观各向同性岩体中圆形巷道的位移解析解，见式(1)[14-15]。

(1)

式中：a为圆形巷道的半径；r和θ为极坐标系下的半径和极角，θ为由x轴的正向算起，沿逆时针旋转的角度；E、μ分别为各向同性面(xoy平面)内的弹性模量、泊松比；E′、μ′分别为垂直各向同性面(oz轴方向)方向的弹性模量、泊松比。

根据位移反分析唯一性理论，张志增推导得到了地应力p和q时的反分析表达式，见式(2)[17]。

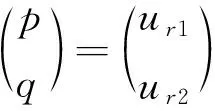
(2)

式中：ur1、ur2分别为两个点(r1,θ1)、(r2,θ2)的岩体位移值。可以看出，同时反分析地应力p和q时，至少需要已知两个测点的位移值和各岩体参数值。

应用数值计算软件FLAC3D建立一个横观各向同性岩体中圆形巷道模型，计算参数如下：a=2 m，E=1 GPa，E′=0.8 GPa，μ=0.25，μ′=0.3，p=10 MPa，q=20 MPa。经FLAC3D计算得到该模型的位移云图如图3所示，由位移云图可以读取出模型中任意点的位移值。

选取点(2，0)和点(2，45)的位移值ur1=0.0589 m和ur2=0.0368 m用于反分析计算。将模拟参数带入式(2)中，求得竖向地应力p=9.916 MPa，水平地应力q=19.524 MPa。与精确值相比相对误差分别为8.4%和2.4%，这证明了反分析的结果的精确度。下面通过调整不同参数的数值，分析各岩体参数对反分析结果的影响。

2.2 各向同性面内的弹性模量E对反分析结果的影响分析

假定对地应力反分析结果有影响的岩体参数中除弹性模量E外均为精确值，通过改变E的参数取值，对E赋予不同的值围绕精确值进行波动，分别计算反分析结果。将E波动时反分析得出的地应力值与E精确时反分析得出的地应力值进行对比，其误差分析结果见表1；再将E波动时反分析得出的地应力值与标准地应力值进行对比，其误差分析结果见表2。E波动时反分析得出的地应力值与E精确时反分析得出的地应力值的相对误差趋势见图4，与标准地应力值之间的相对误差趋势见图5。

由表1、表2、图4和图5可知，弹性模量E的取值波动对反分析结果的影响呈现出一定的线性相关性，参数取值的误差越大，反分析所得结果误差越大。从指导工程应用的角度来看， 弹性模量E的取值精度控制在10%内时， 反分析所得结果的相对误差较小，此时反分析所得结果仍具有可信度。

图3 横观各向同性岩体中圆形巷道模型的位移云图

表1 E波动时反分析所得地应力值与E精确时 反分析所得地应力值对比

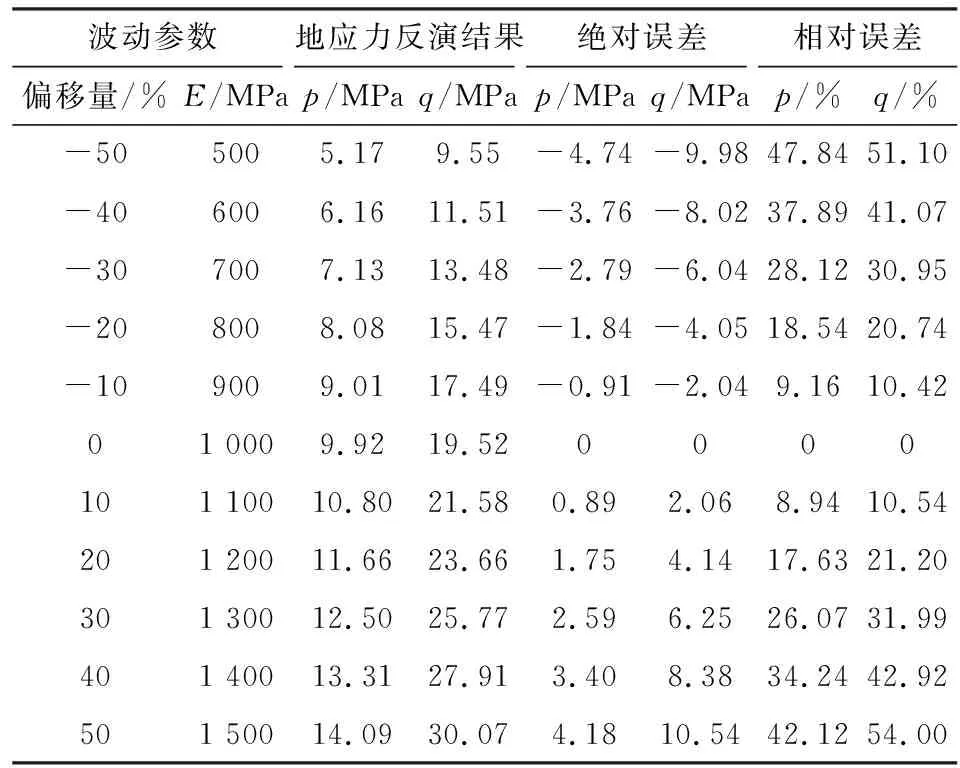
波动参数地应力反演结果绝对误差相对误差偏移量/%E/MPap/MPaq/MPap/MPaq/MPap/%q/%-505005.179.55-4.74-9.9847.8451.10-406006.1611.51-3.76-8.0237.8941.07-307007.1313.48-2.79-6.0428.1230.95-208008.0815.47-1.84-4.0518.5420.74-109009.0117.49-0.91-2.049.1610.4201 0009.9219.520000101 10010.8021.580.892.068.9410.54201 20011.6623.661.754.1417.6321.20301 30012.5025.772.596.2526.0731.99401 40013.3127.913.408.3834.2442.92501 50014.0930.074.1810.5442.1254.00

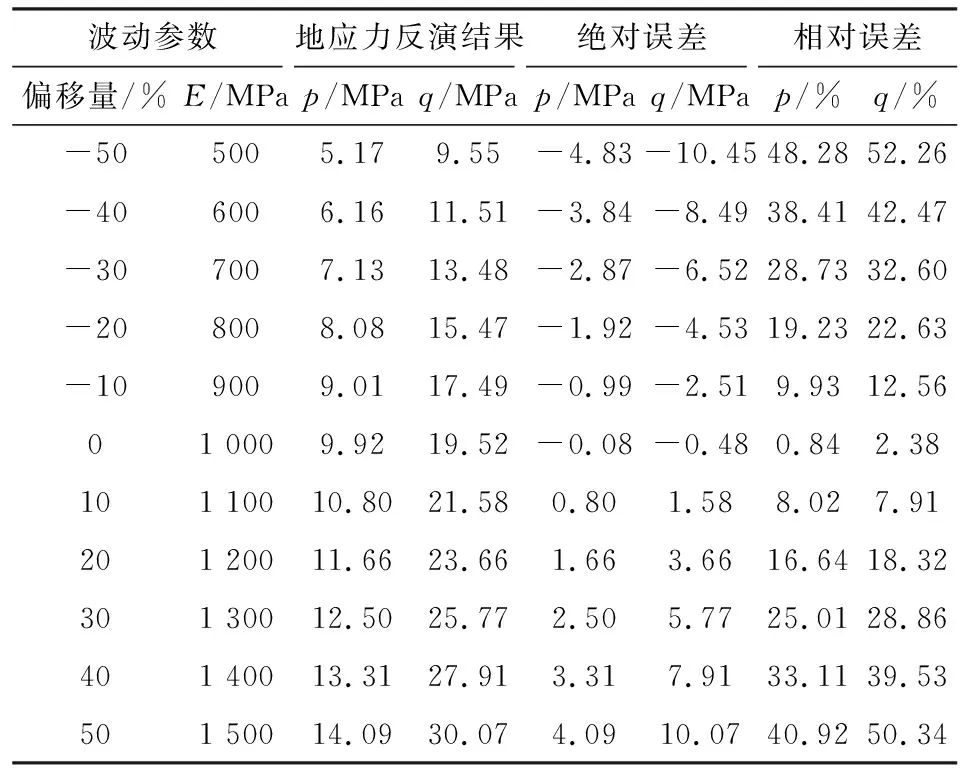
表2 E波动时反分析所得地应力值与标准地应力值对比

图4 E波动时反分析所得地应力值与E精确时 反分析所得地应力值的相对误差趋势

图5 E波动时反分析所得地应力值与标准地 应力值的相对误差趋势

2.3 各向同性面内的泊松比μ对反分析结果的影响分析

假定对地应力反分析结果有影响的岩体参数中除泊松比μ外均较为精确，通过改变泊松比μ的参数取值，对μ赋予不同的值围绕精确值进行波动，分别计算反分析结果。将μ波动时反分析得出的地应力值与μ精确时反分析得出的地应力值进行对比，其误差分析结果见表3；再将μ波动时反分析得出的地应力值与标准地应力值进行对比，其误差分析结果见表4。μ波动时反分析得出的地应力值与μ精确时反分析得出的地应力值之间的相对误差趋势见图6，与标准地应力值之间的相对误差趋势见图7。

表3 μ波动时反分析所得地应力值与μ精确时 反分析所得地应力值对比分析

表4 μ波动时反分析所得地应力值与 标准地应力值对比分析

图6 μ波动时反分析所得地应力值与μ精确时 反分析所得地应力值的相对误差趋势

通过表3、表4、图6和图7的分析结果可以看出，泊松比μ的取值波动对反分析结果的影响呈现出一定的线性相关性，参数取值的误差越大，反分析所得结果误差越大。从指导工程应用的角度来看，泊松比μ的取值精度控制在30%内时，反分析所得结果的相对误差较小，此时反分析所得结果仍具有可信度。

2.4 垂直各向同性面方向的弹性模量E′对反分析结果的影响分析

假定对地应力反分析结果有影响的岩体参数中除弹性模量E′外均较为精确，通过改变弹性模量E′的参数取值，对E′赋予不同的值围绕精确值进行波动，分别计算反分析结果。将E′波动时反分析得出的地应力值与E′精确时反分析得出的地应力值进行对比，其误差分析结果见表5；再将E′波动时反分析得出的地应力值与标准地应力值进行对比，其误差分析结果见表6。E′波动时反分析得出的地应力值与E′精确时反分析得出的地应力值之间的相对误差趋势见图8，与标准地应力值之间的相对误差趋势见图9。

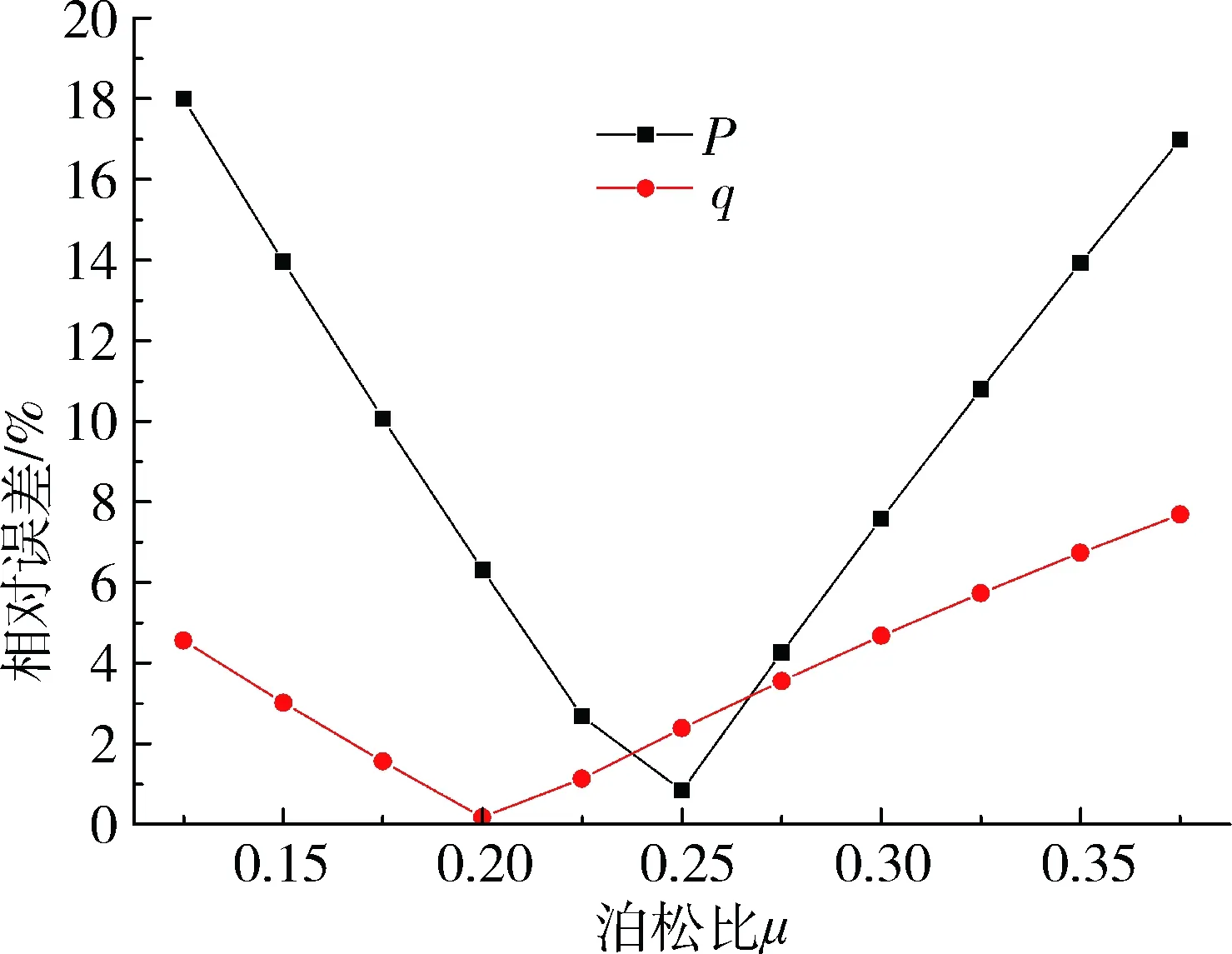
图7 μ波动时反分析所得地应力值与标准地 应力值的相对误差趋势

表5 E′波动时反分析所得地应力值与E′精确时 反分析所得地应力值对比分析

波动参数地应力反演结果绝对误差相对误差偏移量/%E'/MPap/MPaq/MPap/MPaq/MPap/%q/%-504008.7520.69-1.171.1711.795.99-404809.2020.25-0.720.727.273.69-305609.4819.96-0.440.444.432.25-206409.6719.77-0.250.252.491.27-107209.8119.63-0.110.111.080.5508009.9219.5200001088010.0019.440.08-0.080.850.432096010.0719.370.15-0.151.530.78301 04010.1219.320.21-0.212.091.06401 12010.1719.270.25-0.252.571.30501 20010.2119.230.29-0.292.971.51

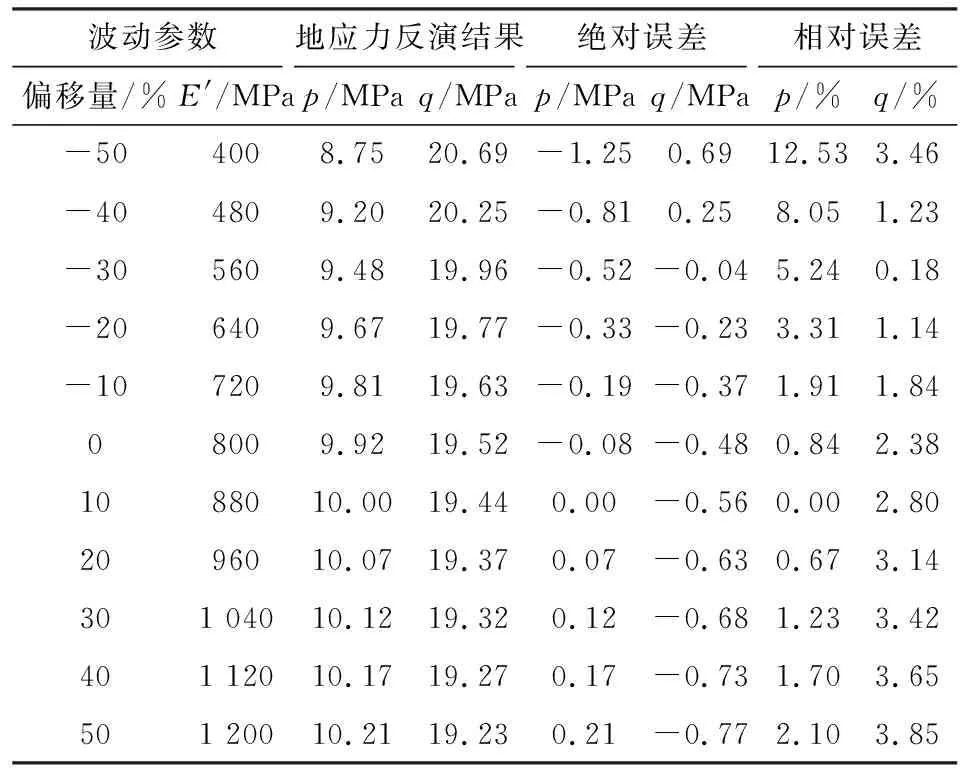
表6 E′波动时反分析所得地应力值与 标准地应力值对比分析

图8 E′波动时反分析所得地应力值与E′精确时 反分析所得地应力值的相对误差趋势

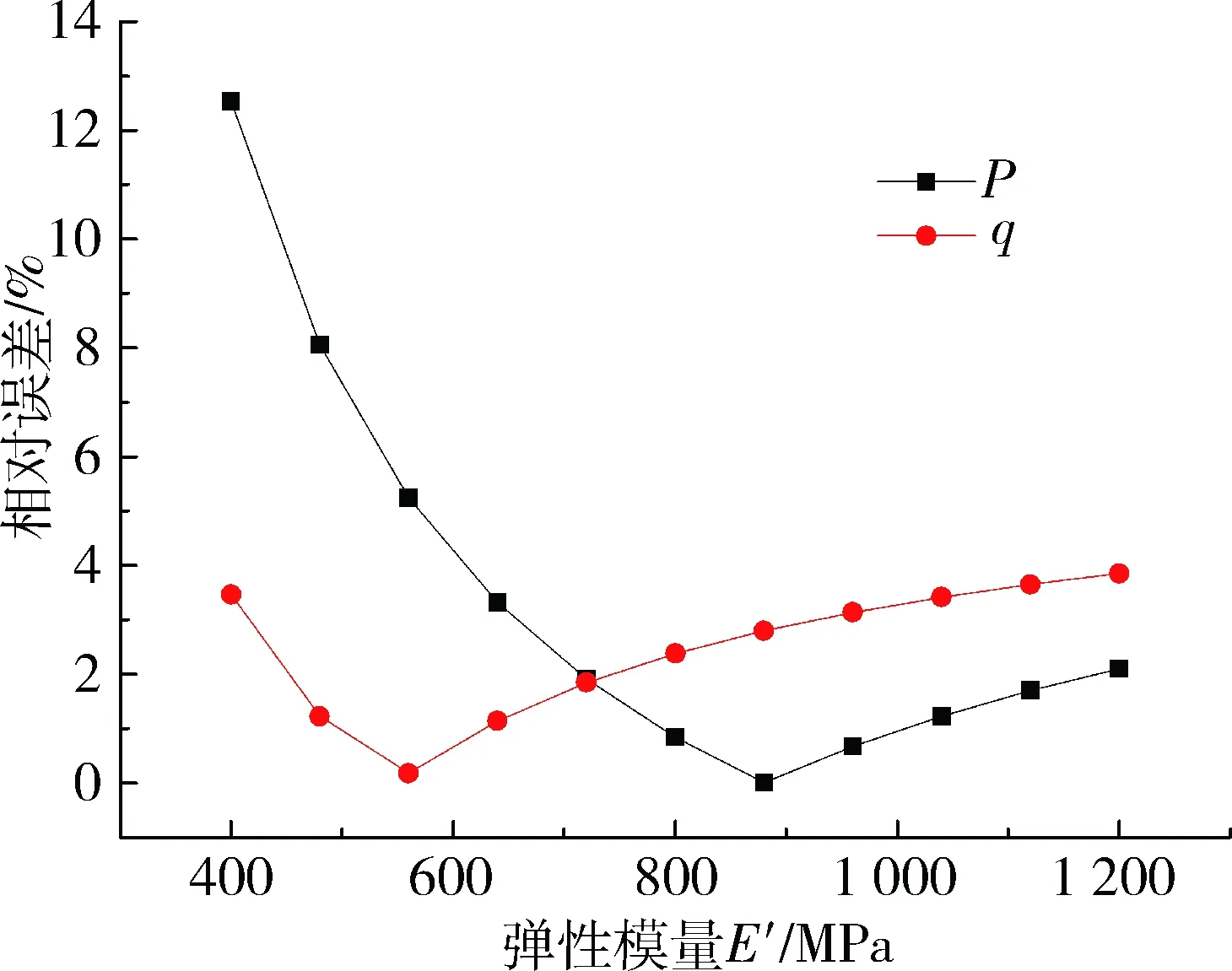
图9 E′波动时反分析所得地应力值与标准地 应力值的相对误差趋势

通过表5、表6、图8和图9的分析结果可以看出，弹性模量E′的取值波动对反分析结果的影响呈现出一定的线性相关性，参数取值的误差越大，反分析所得结果误差越大。从指导工程应用的角度来看，弹性模量E′的取值精度控制在50%内时，反分析所得结果的相对误差较小，此时反分析所得结果仍具有可信度。

2.5 垂直各向同性面方向的泊松比μ′对反分析结果的影响分析

假定影响地应力反分析结果的岩体参数中除泊松比μ′外均较为精确，通过改变泊松比μ′的参数取值，对μ′赋予不同的值围绕精确值进行波动，分别计算反分析结果。将μ′波动时反分析得出的地应力值与μ′精确时反分析得出的地应力值进行对比，其误差分析结果见表7；再将μ′波动时反分析得出的地应力值与标准地应力值进行对比，其误差分析结果见表8。μ′波动时反分析得出的地应力值与μ′精确时反分析得出的地应力值之间的相对误差见图10，与标准地应力值之间的相对误差趋势见图11。

通过表7、表8、图10和图11的分析结果可以看出，泊松比μ′的取值波动对反分析结果的影响呈现出一定的线性相关性，参数取值的误差越大，反分析所得结果误差越大。从指导工程应用的角度来看，泊松比μ′的取值精度控制在40%内时，反分析所得结果的相对误差较小，此时反分析所得结果仍具有可信度。

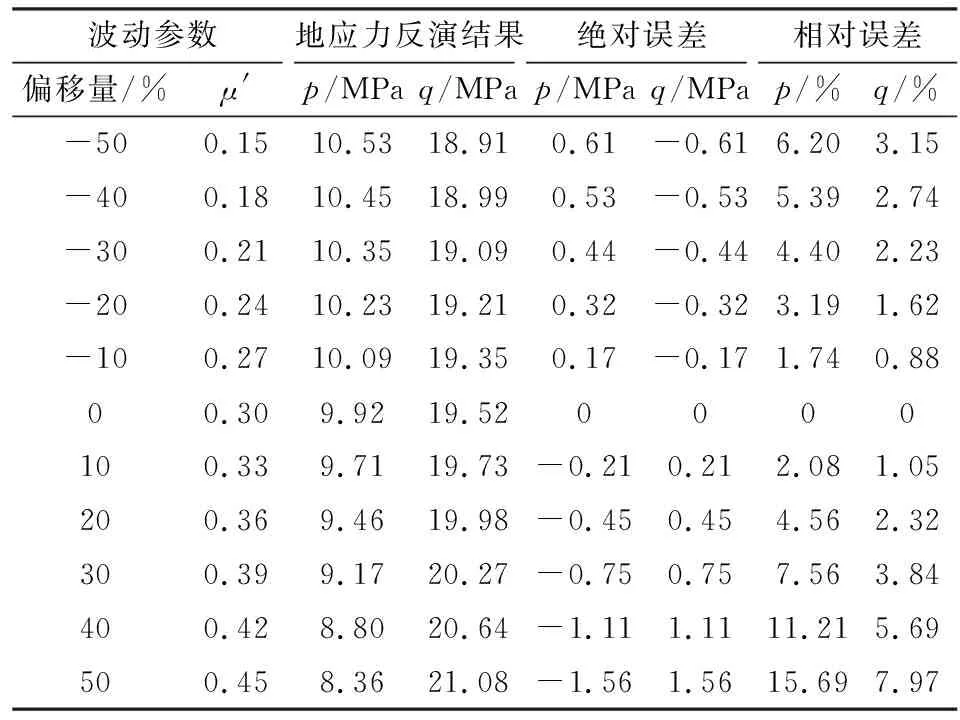
表7 μ′波动时反分析所得地应力值与μ′精确时 反分析所得地应力值对比分析

表8 μ′波动时反分析所得地应力值与 标准地应力值对比分析

图10 μ′波动时反分析所得地应力值与μ′精确时 反分析所得地应力值的相对误差趋势

图11 μ′波动时反分析所得地应力值与标准地 应力值的相对误差趋势

3 结 论

1) 在反分析结果具有唯一性的前提下，横观各向同性岩体深埋圆形巷道反分析模型能够通过位移解析解进行地应力反分析计算，其结果是可靠的。

2) 应用横观各向同性岩体深埋圆形巷道位移解析解建立反分析模型进行地应力反分析计算时，已知岩体参数的精度对地应力反分析结果的影响呈现出线性相关性，参数的误差越大，所得反分析结果精度越低。

3) 横观各向同性岩体中深埋圆形巷道反分析模型地应力反分析的参数敏感程度如下：弹性模量E的精确度对反演值结果影响最大，泊松比μ次之，泊松比μ′再次之，弹性模量E′影响最小，其误差分别在10%、30%、40%、50%以内时反分析的结果仍具有可信度。

4) 在使用横观各向同性岩体深埋圆形巷道位移解析解建立反分析模型进行地应力反分析计算时，应重点控制横观各向同性面的参数弹性模量E取值的精度，且注重提高其余参数的精度，以确保反分析结果的精度。