双方参与的随机数生成和验证方案
刘建湘,刘忆宁
1.长沙理工大学 计算机与通信工程学院,长沙 410076
2.桂林电子科技大学 可信软件重点实验室,广西 桂林 541004
1 引言
密码技术被广泛地应用于信息系统中,以保证信息的安全性、完整性、可处理性、可传递性和不可否认性。随机数是密码技术应用的一个重要部分,密钥协商[1-2]、密钥管理[3]、数字签名[4-6]和身份认证[7]等都需要随机数参与。随机数分为真随机数和伪随机数。真随机数是利用手工方法或物理方法选取随机源产生的随机数,真随机数因产生速度慢、缺乏可移植性、通信双方同步困难,不适合大规模的使用。伪随机数是利用数学算法[8-10]产生的随机数,由于其依照特定算法产生的,并不是真正的随机数,但由于其周期很长,在现实中可以看成是没有反复满足各项指标的随机数。目前在计算机系统中使用的随机数,基本上都是伪随机数。除了真随机数、伪随机数,在不少电子商务的场合,还需要可验证随机数,即不仅需要其结果是随机的,而且要求这种随机性能被验证。真随机数当然不具可验证性,伪随机数的验证则需要提供随机数生成算法及种子给验证者,这当然是不现实的。比如在电子彩票[11]中,可信第三方可以产生不受人为因素控制的随机数中奖号码,彩票发行机构不能预知彩票中奖号码,杜绝了彩票发行机构和彩票购买者合谋从而牟取非法利益的情况,这需要随机性来保障。但仅仅这样还不够,如果彩票购买者无法验证中奖号码是否是随机的,就有理由对结果提出质疑,从而影响了彩票发行的信誉。刘忆宁等提出了基于可验证性随机数的电子彩票方案[12],满足可验证性。
关于如何产生满足要求的随机数始终是研究热点[13-15],主要是利用RSA和BDH的困难性问题生成可验证性随机数,但是RSA和BDH的困难性问题都需要复杂的运算,效率不高。刘忆宁的方案则是基于有限域上插值多项式的可验证随机数方案[16],方案中n个用户共同生成一个随机数r,而且用户能够验证自己参与生成随机数r。每个用户选择一对随机数并发送给计算中心CC。CC收到后,加上自己任选的,依据这n+1个点构造一个n次插值多项式a0,其中令,CC公布可验证性随机数r。在上述方案中,随机数r的生成,虽然满足了安全性、可验证性,但需要可信的计算中心。随着随机数应用环境的不断变化,多方参与的可验证性随机数,不能很好地满足两方参与随机数生成的相关要求。
本文利用单向函数设计了面向双方的可验证性随机数方案,双方平等参与随机数的生成,并且都可以验证自己参与了生成,协议的安全性不需要计算中心或可信第三方,降低了计算消耗及通信瓶颈,具有可验证性、公平性、安全性、高效性、适用性。
2 单向函数
2.1 单向函数的基础知识
单向函数是密码学领域中的一个基本要素,其存在性意味着安全密码系统的存在性。由于单向函数特殊的性质,其被广泛应用到安全协议,如在电话掷币协议、承诺协议。协议是指多个参与实体之间执行的规程,具有适当的定义。单向函数在保证协议安全执行的过程中发挥着重要作用。单向函数 f()x具有性质如下:
(1)对于任意的整数x,由x计算 f(x)是容易的;而给出 f(x)计算x是不可能的。
(2)不可能找出一对整数 x1,x2,满足且
在单向函数的应用中,假设有两方(A和B)来参与执行协议。参与方A利用单向函数 f(x)和信息x计算:y=f(x),并且将y发送给B。当A公开信息x,B验证A发送的y。这个过程必须满足以下特性:
(1)隐私性:在公开信息x之前,任何人(除A以外)无法得到信息x。
(2)绑定性:在计算并发送y之后,任何人(包括A)无法改变x。
(3)可验证性:公开信息x之后,任何人都可以验证信息x,并且A无法否认。单向函数的性质使其得到广泛的应用,如:零知识证明、安全多方计算、身份认证等。
单向函数在这里的作用,主要是使用其绑定性,事实上是数据承诺的功能,可把单向函数看成是承诺的一个特例。
2.2 单向函数的应用实例
Hash函数是一种单向函数,即y=h(x),由x计算y是简单可行的,但由y计算x是不可行的。根据这一特性,可以用Hash函数。Alice利用Hash函数实现可验证性,具体步骤如下:
步骤1 Alice根据消息x计算y=h(x),是一种Hash函数。
步骤2 Alice把 y发给Bob。
步骤3 Alice需要公开信息x时,将x发给Bob。
步骤4 Bob计算 y′=h()x ,比较 y′=y是否成立,从而实现可验证性。
利用Hash函数的单向性,在公开信息x之前,Bob无法得到x,也无法改变x。在公开信息x之后,Bob可以验证y是由x生成的。
3 双方参与的随机数生成和验证方案
利用单向函数,构造双方参与的随机数生成方案和验证方案,双方都可以验证自己参与了随机数的生成,并且实现了安全性、高效性、公平性、可验证性、适用性、随机性、不可伪造性、不可预测性。该方案中有两个参与者:Alice和Bob。Alice和Bob需要协商一个随机分布于区间[a ,b]上的整数,整数出现是相互独立的。随机整数不能由一个参与方单独控制大小,但双方都可以验证自己参与随机数的生成。假设在生成随机数之前,[a ,b]和单向函数h(⋅)是公开的参数,且双方之间不存在合谋的可能,因为只有两方参与,他们的合谋是没有意义的。
方案分为随机数生成阶段和随机数验证阶段。
3.1 随机数生成阶段
步骤1 Alice向Bob发送请求,要求生成随机数。
步骤2 Bob选择的随机数r2,计算y2=h(r2),并将y2发送给Alice。
步骤3 Alice收到 y2后,选择随机数r1并发送给Bob。Bob计算 R=h(r1,r2)mod(b-a)+a+1。Bob令 R为双方协商的随机数,并将其发送给Alice。
3.2 随机数验证阶段
Alice怀疑Bob公布的随机数R时,Alice可以申请验证R。
步骤1 Alice对Bob提出申请,要求验证R。
步骤2 Bob把r2发送给Alice。
步骤3 Alice收到r2,计算 R′=h(r1,r2)mod(b-a)+a+1和,判断R′=R和是否成立,从而验证是否参与生成R。
双方参与的随机数生成和验证方案可以生成满足双方要求的随机数,并且随机数是均匀分布在区间[ ]a,b上的,而且每个整数出现是相互独立的。该方案满足安全性、随机性、公平性、可验证性、不可伪造性、高效性、不可预测性,另外该方案还具有较强的使用性,不论在双方参与还是多方参与都具有适用性和高效性。
3.3 实例应用
双方参与的随机数生成和验证方案在实际生活中有着广泛的应用,例如构造可验证性随机数电子优惠卷、电话掷币等。假设在随机数电子优惠券方案中,有两个参与者:用户(U)和商家(M)。首先M通过公共渠道发布优惠信息,任何用户在该商店购买商品,当商品价格大于m时,用户使用电子支付均可通过抽奖获取1到m元的电子优惠券。方案分为优惠券金额生成阶段和优惠金额验证阶段。
3.3.1 优惠金额生成阶段
U在M处购买商品,看到商家发布的优惠信息,决定电子支付,并和商家一起生成电子优惠券。
步骤1U向M发送支付请求,M选择随机数r2,计算y2=h(r2),并将y2发送给U。
步骤2U收到y2后,选择随机数r1并发送给M。
步骤3M计算R=h(r1,r2)modm+1,令R为双方生成的优惠金额值,并在U的支付账单中减少R。
3.3.2 优惠金额验证阶段
U使用电子支付时,如果怀疑商家每次恶意的分配小金额优惠券,可以申请验证R。
步骤1U对M提出申请,要求验证R。
步骤2M把r2发送给U。
步骤3U收到r2,计算R′=h(r1,r2)mod(b-a)+a+1和,判断R′=R和是否成立,从而验证是否参与生成优惠金额值R。
4 分析
4.1 安全性分析
在整个过程中,Alice和Bob只交换了随机数,并没有个人信息的交换,Alice和Bob无法获取对方的个人信息,外部恶意攻击者无法得到Alice和Bob的个人信息,不存在隐私信息的泄露。对Alice和Bob来说,该方案保护了双方的身份隐私性。
随机数的生成是相互独立的,并且不受Alice和Bob的控制,对与Alice和Bob来说随机数是安全的。实例中,用户和商家生成了区间上的随机优惠值,并且其中一方无法控制随机数的生成,而且用户还可以验证自己参与优惠值的生成。整个方案中只有随机数的交换,商家和用户无法损害对方利益,外部恶意攻击者也不会损害到用户和商家的利益。
4.2 公平性分析
实例中,U和M共同参与生成优惠值R,并且U可以验证自己参与了生成优惠值。U收到y2后,无法根据y2得到r2,也就无法选择期望的随机数r1,所以用户无法控制优惠值的生成。M无法根据r1的大小来改变r2的大小,从而得到期望的R值,所以M无法控制优惠值的生成,防止了M恶意分配小额优惠值,保证了双方在交易过程中的公平性。
4.3 可验证性分析
Alice对Bob公布的随机数产生了怀疑,可以申请验证。Alice根据判断R′=R和是否成立从而验证自己是否参与了随机数的生成。另外Bob将y2发送给Alice,Alice无法根据y2得到r2,也就无法选择期望的随机数r1,双方都无法控制随机数的生成,并且双方都可以验证参与了随机数的生成,满足可验证性。
实例中,用户可以验证自己是否参与了优惠值的生成,满足了可验证性。
4.4 不可伪造性分析
分布于区间上的随机数R是由随机数r1和r2共同生成的。随机数r1和r2分别是Alice和Bob随机选取的,并且选取之后,Bob无法更改r2,生成的随机数满足不可伪造性。
4.5 适用性
双方参与的可验证随机数生成方案不仅适用于双方,还可以多方选择随机数来生成共同使用的随机数。基于插值多项式的随机数生成方案中,当人数较多时,多项式次数较大,生成多方使用的随机数随着参与方的增加,所需计算量增加较多造成效率较低。而且,插值多项式方案中需要计算中心的参与,因此双方参与的随机数生成和验证方案适用性更好。
4.6 不可预测性
在Alice向Bob发送请求,要求生成随机数。Bob选择的随机数r2,计算 y2=h(r2),并将 y2发送给Alice;Alice无法根据y2计算得到r2,从而选择合适的r1来得到期望的R。Bob选择的随机数r2时,不知道r1的大小,所以无法选择合适的r2来得到期望的R。Bob收到r1后无法更改r2,来得到期望的R,所以随机数R的生成是不可预测的,满足不可预测性。
4.7 高效性
方案主要采用Hash函数做计算,不必要进行高次数的指数运算,具有高效的特性。在方案中,Alice只需要提供随机数r1就可以生成共用的随机数R,和有限域上插值多项式生成随机数的方法相比,减少了计算中心的参与,降低了通讯量。假设1 000个人中有一个Alice要求验证,一个数据是1 000 bit,和插值多项式生成随机数比较,得到结果如表1。
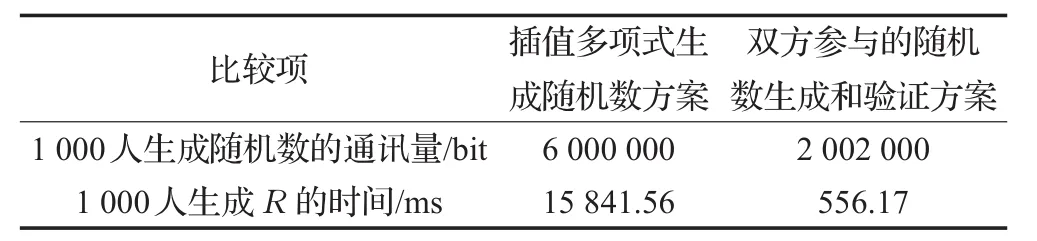
表1 1 000人生成随机数的通讯量比较
由表1可知,双方参与的随机数生成和验证方案在计算时间和通讯上更加高效。另外基于插值多项式生成随机数方案中人数成倍数增加时,生成可验证性随机数的计算负担发幅度增加。利用电脑参数为:系统Ubuntu 14.0403LTS,CPU:2.50 GHz,内存:8 GB的电脑分别计算生成可验证性随机数的时间,得到结果如表2,本文单向函数以SHA-256为例。
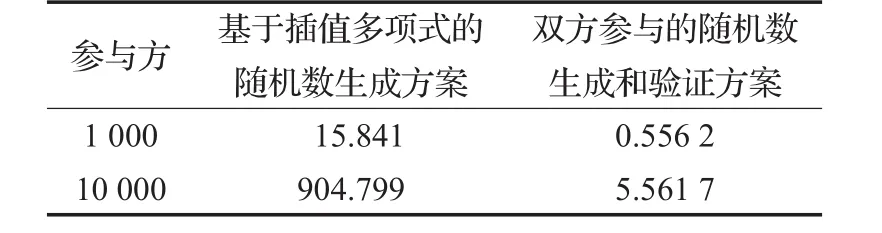
表2 生成可验证性随机数R的时间ms
5 总结
双方参与的随机数生成和验证方案将Bob作为计算中心,Alice只需要提供随机数r1即可参与随机数R的生成,运算过程中无需计算中心和可信第三方参与。在随机数R公布之后,Alice如果需要验证,Bob把自己选择的随机数r2和时间t发送给Alice,Alice做Hash运算从而验证。因此,用户承担的计算量、通讯量都得到了降低,该方案比较适用于移动终端的使用。

