室内外一体化最优路径分析算法实现

张文元，丁京祯，杨丽娜，杨翔宇

1.华中师范大学 国家文化产业研究中心，武汉 430079

2.中国科学院 遥感与数字地球研究所，北京100864

1 引言

为出行者提供路径规划与导航服务的各种应用层出不穷，但目前大部分应用仅限于城市室外交通网络。随着城市化进程加速，室内空间的开发与利用得到了增强，公众在室内空间的活动范围和时间也相应增多，如购物中心、政务中心、机场、火车站、医院和博物馆等大型公共建筑都是人流密集的区域。陌生而又错综复杂的大型公共建筑加剧了空间认知负担，使得人们在这些公共场所内部的寻路愈加困难[1]。如何将宏观的室外空间与微观的室内环境集成在一起进行路径分析，满足公众日益强烈的室内外一体化路径查询需求，并为室内空间发生火灾等突发事件的应急响应提供最佳救援路径，已经成为了智能交通和地理信息科学领域的一项研究热点和挑战，也是当前智慧城市建设的一项重要内容。

最优路径分析是GIS（Geographic Information System，地理信息系统）空间分析的重要组成部分，其正确性、灵活性和高效性直接关系到智能空间信息服务质量。由于室内空间涉及多层建筑，室内网络数据要比室外道路网络复杂，传统的基于室外二维道路网络连通模型的路径分析方法并不直接支持室内空间复杂的三维拓扑构建和路径分析。在室内路径分析方面，已有一些学者进行过研究。Lee[2]将室内空间中的房间、门和楼梯出入口等实体统一抽象为节点，节点之间通过走廊、电梯或楼梯建立连接关系，从而构建室内三维网络连通拓扑模型，并采用改进的Dijkstra算法来实现室内三维最短路径分析。Becker等[3]将室内空间分为多个层次，建立多层次拓扑模型来表达室内空间关系及拓扑结构。Tsiliakou等[4]利用CityEngine构建建筑物三维模型，并通过为矢量线路数据集的每个坐标点增加Z值来建立三维室内路径模型，最后基于ArcGIS软件自带的网络分析工具实现了室内三维空间的路径查询。林浩嘉等[5]根据多层建筑的三维空间特性，将各楼层路网和楼层之间的连接视为独立结构，根据停靠点的楼层分布情况逐楼层动态构建网络模型，提出一种分层结构化的动态网络分析方法来实现多层建筑的最短路径规划。林巍凌[6]针对传统路径规划算法的局限性，提出一种基于Delaunay三角剖分导航网格的A*算法，用于室内导航路径规划。该算法虽然能自动构建室内导航网格，但是算法复杂性高，正确性需要人工验证，而且针对一些特殊情况难以自动处理。刘涛等[7]利用矢量建筑图自动构建室内建筑、地标的可视关系，以此建立行人导航通行规则，并利用多目标蚁群算法实现了一种顾及地标可视性的室内导航路径优化算法。该方法对初始数据要求较高，并且在构建拓扑网络时需要人工定义多种规则。

尽管对室内路径分析已有一些研究成果，但是大多需要构建特殊的网络数据模型，并采用改进的路径分析算法来处理，算法复杂，面对大规模网络数据的实时查询还存在性能问题，并且难以适应传统的室外交通网络分析。而如何实现室外地图与室内通行地图的无缝对接，并提供室内外一体化最优路径分析服务，相关研究和应用非常少。本文针对室内外路网数据各自的特点，提出一种室内外一体化道路网络数据模型，并对开源路径分析算法库pgRouting进行扩展，实现了室内外一体化最优路径查询分析和二维可视化展示，方法简单高效，普适性强。

2 室内外一体化路径数据模型

构建具有几何拓扑关系的网络数据模型是实现室内外一体化最优路径分析算法的基础。考虑到目前广泛采用的导航电子地图都是二维的，并且在二维平面上显示路径简洁高效，为了最大限度保持与现行主流交通网络数据结及Dijkstra等一些成熟路径分析算法的兼容，本文设计了一种较为通用的室内外一体化几何网络数据模型。

2.1 室内外一体化路径数据模型设计

在室内导航网络模型方面，目前主要有四类[8]：（1）几何网络模型（Geometric Network Model，GNM）；（2）可导航空间模型（Navigable Space Model）；（3）细分方法模型；（4）规则格网模型。其中，GNM[9]是对节点关系图（Node-Relation Graph，NRG）的扩展，不仅能够表达室内三维对象之间的邻接、连通和层次等逻辑关系，而且还能精确表达其几何属性，其结构相对简单，因而广泛应用于室内网络分析。因此，本文参照文献[9]提出的GNM及骨架抽取算法来快速构建室内对象的几何网络模型。但与该文献的3D-GNM不同，为了最大限度保持与现行主流城市交通网络数据模型的一致性，并兼容Dijkstra等一些成熟的路径分析算法，本文设计了一种楼层数据偏移策略，并在此基础上采用2D-GNM来表达室内三维空间的路径几何网络。

首先，根据所获取的建筑内部平面布局设计图，将走廊、过道等通行路径抽象为线要素，用其中轴线表示；将走廊拐角、楼梯出入口、电梯出入口、房间出口等对象抽象为点要素，这些点要素与线要素相互连接构成节点-边网络图。在构建GNM模型过程中，走廊和过道等矢量要素的中轴线参考S-MAT（Straight-Medial Axis Transformation）骨架线提取算法，它是对传统泰森多边形（Voronoi图）构建法和中轴变换（MAT）的改进，降低了算法复杂性，并且可以避免线要素在相交处出现变形等问题，如图1所示。

图1MAT与S-MAT中轴变换法比较

图2 展示某个楼层数据经过抽象提取后的GNM模型，红色虚线表示中轴通行路径，与中轴线连接的节点表示路径上的各类出口和拐点。

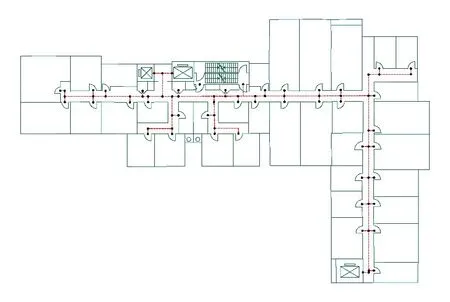
图2 楼层平面通行路径网络数据模型示例

单个楼层路径网络模型构建完成之后，再将电梯或楼梯等楼层实际连接物抽象为线要素，与楼层平面图中的电梯或楼梯出入口等点要素连接，从而构建室内垂直方向的通行拓扑网络。但是，如何使用2D-GNM对室内多层路网模型进行合理的可视化表达也是一大挑战。为此，本文设计了一种数据偏移策略，对室内不同楼层的数据进行地理偏移处理，即：针对同一楼宇1楼以上的各个楼层平面图数据，利用如下公式将每个数据点的二维坐标(x,y)沿Y轴方向进行平移变换，形成新的坐标 (x′,y′)：

其中，f代表楼层号，f∈[1,N],N为建筑物楼层数。d代表楼层之间的间隔长度（层高），单位为m。s代表缩放因子，目的是使得偏移后的第i层与i-1层数据没有重叠。

基于该策略，f=1时，表示建筑物1楼平面数据不进行偏移处理，直接在该建筑物外部轮廓范围内显示。f＞1时，位于2楼及以上楼层的平面数据横坐标不变，纵坐标偏移量随楼层数的增加而逐步增大，从而使得多层建筑的室内地图数据呈现出立体表达的可视化效果。经过偏移处理后，不仅每个楼层平面上要素之间的拓扑关系保持不变，而且衔接不同楼层的垂直空间拓扑关系一目了然，如图3所示。

图3 经过坐标偏移处理的室内多层路网数据模型示意图

此外，设计的坐标变换程序包含正变换和逆变换两个函数，利用正变换进行偏移可满足路径分析和可视化表达需要，而通过逆变换将偏移后的坐标还原为真实坐标，可满足导航定位和真实路径方向描述的需求。2DGNM模型中的每条边和每个点除了具有空间位置几何特征、平面方向和垂直方向相互连通的拓扑关系外，还包括名称、类型、所在楼层、所在建筑物和权重等语义信息。

基于2D-GNM的室内多层路网模型构建完成之后，为了支持室内外一体化的路径分析，需将室内多层路网数据在地面一楼的出入口与外部道路网络数据进行连接，即可形成一套完整的室内外一体化路径几何网络数据模型。该模型不仅支持利用现有的二维网络图搜索算法进行路径分析，而且满足室内三维数据在二维空间的近似表达。

2.2 网络通行成本

网络通行成本是计算交通几何网络模型中两点之间最优通行路径的关键。针对室内外一体化路径分析，本文主要考虑距离（Length）和时间（WalkTime）两类通行成本。其中，对于网络中的室外路径以及室内水平方向上的边要素，根据其几何长度赋予距离成本；而室内垂直方向的电梯或楼梯等边要素，则需要根据楼层之间的高度和楼梯的实际量算长度来分别为其设置距离成本。对于时间成本，依据网络边要素的距离以及不同道路类型上的平均步行速度来计算。本文结合相关文献给出的参考数据[10-11]，考虑4种不同道路类型的步行平均速度V ：（1）室外道路，设定Vout=1.4 m/s；（2）室内走廊等水平通行路径，Vhor=1.2 m/s；（3）室内连接不同楼层的楼梯，设定上行Vstair=0.9 m/s，下行Vsatir=2.0 m/s；（4）室内垂直电梯，设定电梯运行的平均速度Vlift=2.5 m/s（考虑等候时间）。确定了网络中每条边要素的距离成本和道路类型之后，可以依据如下公式自动计算网络中各条边的时间成本：

式中Te代表边要素步行时间，Le代表边长度，Ve代表该边要素的步行速度。

这样，计算网络上任意两点间最快通行路径就转化为求解网络上累计时间成本最小的路径问题，公式如下：

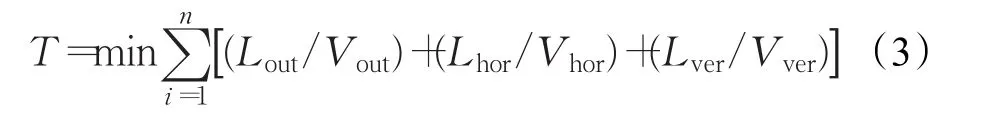
式中，T表示总通行时间，i为结果路径上的每一条边，Lout为室外道路的长度，Lhor代表室内水平路径的长度，Lver代表室内垂直路径的长度，如电梯或楼梯，Vver代表室内垂直路径的速度，Vver=Vstair或Vver=Vlift。

以图4所示的上下两层楼部分路径网络为例，从1楼到2楼乘坐电梯上下行的时间成本均为1.2 s，而步行上楼需要20 s，步行下楼成本为8 s。在计算跨楼层的最快路径时，会优先选择乘坐电梯。

图4 室内不同楼层几何网络时间成本示意图

2.3 几何网络模型数据存储

针对制作完成的室内外一体化路径几何网络模型数据，本文采用邻接表数据结构在开源对象关系型数据库系统PostgreSQL[12]进行存储和管理。邻接表采用链式结构存储网络拓扑，相对于邻接矩阵优化了存储空间，降低了空间复杂度，是交通网络表达中一种高效的数据结构[13]。PostgreSQL中主要存储路网模型边数据表（route）和对应的节点数据表（route_vertices_pgr）。其中，route表逻辑结构设计如表1，除了基本属性外，还包括RouteType、IsInside、BuildingID和FloorID等扩展语义属性，满足网络成本计算、坐标偏移、路径方向描述和分段可视化等需要。route表的Source和Target字段存储边要素的起点和终点编号，关联route_vertices_pgr表的ID（主键）字段，以此表达网络拓扑关系。这种存储方式将路径网络模型中的空间数据、属性数据和拓扑数据进行了有机关联，并且采用拓扑邻接表存储结构的空间复杂度仅为O(e+n)，e和n分别表示边和节点数量，即使边信息表属性较多对存储空间也没有影响，可以适应大规模交通网络。

3 基于开源pgRouting的最优路径分析算法

计算二维平面网络中两点之间的最优路径可以归结为图论中求解带权有向图的最短路径问题，Dijkstra算法[14]、A*算法[15]、遗传算法[16]和禁忌搜索算法[17]等一些经典的图搜索算法可用来解决该问题。本文主要基于经典的Dijkstra算法理论和开源路径分析算法库pgRouting[18]实现室内外一体化最优路径分析。

3.1 Dijkstra算法思想

Dijkstra算法是目前公认的求解单源最短路径问题的最佳算法[19]，也是许多GIS系统解决最短路径问题的理论基础，例如ArcGIS的Network Analysis模块就使用了该算法。

Dijkstra算法思想为：设G=(V,E)是一个带权有向图，V表示所有顶点集合，E表示所有边集合，E中的每一条边E(i)是由V中的两个点所形成的有序元素对。假设(u,v)表示从顶点u到v有路径相连，w(u,v)代表从顶点u到顶点v的权重。Dijkstra算法要求图中不存在负权边，因而边的权重函数定义为w:E→[0,∞]。G中任意两点间路径的权重就是该路径上所有边的权重总和。把G中顶点集合V分成两组，第一组为已求出最短路径的顶点集合，用S表示，初始时S中只有一个源点v。第二组为其余未确定最短路径的顶点集合，用U表示。Dijkstra算法的关键部分是从U中不断地找出到源点v距离最近的点，并把该点加入到S集合中，同时更新U中其余点到起始点的最短路径距离。按最短路径长度的递增次序依次把U中的顶点加入S中，并总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度，直到全部顶点都加入到S中，算法结束。

3.2 pgRouting最短路径算法

pgRouting是对PostGIS/PostgreSQL地理空间数据库进行扩展的一个开源C语言类库，支持Dijkstra算法、A*算法、Johnson和Floyd-Warshall等多种最短路径分析算法。pgRouting最短路径核心算法基于Boost Graph Library[20]（简称BGL）实现，利用BGL提供的斐波那契堆（Fibonacci Heap）数据结构，将Dijkstra算法的时间复杂度从传统的降低到代表节点数量，|E|代表边数量，大大提高了搜索效率。

表1 route表逻辑结构设计

针对导入PostgreSQL的室内外一体化路径边数据（route），调用pgRouting内置的pgr_createTopology函数自动构建网络拓扑信息，并生成边对应的节点信息表（route_vertices_pgr），同时填充route表每条记录的source和target字段值，从而构建网络拓扑关系。拓扑关系创建成功后，便可使用pgr_dijkstra等函数来查询两点之间的最短路径。

3.3 pgRouting最短路径算法扩展

3.3.1 创建两点间最优路径分析函数

pgr_dijkstra（sql，source，target，directed，has_rcost）函数默认需要输入source和target，但在真实应用场景中，用户根本不知道起止点的ID。为了能够支持通过地图界面交互、兴趣点选择或者当前GPS定位坐标来查询两点之间最优路径，本文对pgr_dijkstra函数进行扩展。具体做法是在PostgreSQL数据库创建自定义函数pgr_fromAtoB，包含6个输入参数：路线表名称（table）、起点坐标(x1,y1)、终点坐标(x2,y2)和查询类型（queryType，0表示距离最短，1表示时间最少）。输出参数为查询结果对应的路段序号（seq）、唯一编号（gid）、名称（name）、成本（cost）、几何形状（geom）和方位角（heading）。

由于用户交互选择的输入点不一定是线路上的节点，函数实现过程中，会首先根据输入点坐标从route_vertices_pgr表查找离该点最近的线路节点。借助PostGIS 2.0为几何对象提供的K-Nearest Neighbour（KNN）索引，在SQL语句中使用<->操作符就可以使用KNN算法快速检索出离输入点(x,y)最近的线路节点，SQL示例为：SELECT id FROM route_vertices_pgr ORDER BY the_geom <->ST_GeometryFromText（''POINT（x，y）''，4326） LIMIT 1。其中，4326 表示WGS1984地理坐标系编号，limit 1表示只输出距离最近的那个节点。

3.3.2 扩展路径方向描述信息

pgr_dijkstra函数返回结果pgr_costResult[]是一个包含{seq,nodeID,edgeID,cost}属性的数组，只有路段序号、节点编号、边编号和成本4个基本属性，能够据此绘制结果线路的几何形状，但是没有路径方向语义信息。方向描述是路径导航的一项重要信息，为了弥补pgRouting在这方面的不足，在上一节自定义函数pgr_fromAtoB中增加了heading参数输出，依据路径中每段线路的起点和终点来计算其方位角。设某段路径的起止点分别为A(x1,y1)和B(x2,y2)，则其方位角计算通用公式为：

Δy＞0且Δx=0时，α=0°

Δx＞0且Δy=0时，α=90°

Δy<0且Δx=0时，α=180°

Δx<0且Δy=0时，α=270°

获取了每条线路的方位角之后，就可以根据相邻两段线路的方位角之差(Δα)来确定转弯方向。为了避免Δα 出现负值，当 Δα<0时，设置 Δα=Δα+360°，使得Δα∈[0°,360°)。本文根据 Δα 取值范围定义8种转弯方向描述信息，如表2所示。这8条规则分别对应图5标记的8个区域。

表2 路径转弯规则定义

图5 路径转弯规则定义示意图

在确定转弯方向的同时，还要考虑线路合并问题。对于相邻两条线路R1和R2，若R1.name=R2.name，且 Δα(R1,R2)∈[0,20)或 [340,360)范围，表示在同一道路上继续直行，则将其合并为一条线路Rnew，设置Rnew.length=R1.length+R2.length,Rnew.walktime=R1.walktime+R2.walktime。最后，将获得的转弯信息和线路名称、线路长度和步行时间等信息共同构成结果路径的方向描述信息，封装成Direction类对象。经过合并处理后仅保留路径中的起点、拐点和终点，简化了路径结果坐标点数量，可以节约内存和网络传输开销，提高客户端绘制效率。

以图6标识的4段线路为例，参照上述转弯规则和路径合并处理规则，就可以将北京路两段线路（2，3）和（3，4）合并为（2，4），仅存储（1，2，4，5）等节点。最终转弯语义描述为：沿南京路向正北方向行驶，然后右转进入北京路，再左转进入陕西路。

图6 依据方位角确定路径方向描述示意图

4 算法实验及结果分析

4.1 系统架构

为了验证室内外一体化几何网络模型和pgRouting扩展路径分析算法的有效性，作者以开源GeoServer[21]（version 2.11.0）为WebGIS服务器，OpenLayers（version 4.2.0）API[22]为地图查询客户端组件，pgRouting（version 2.2.2）为路径分析核心类库，使用Java和JavaScript开发了室内外一体化最优路径查询原型系统。

基于本系统的最优路径分析实现流程如图7所示。

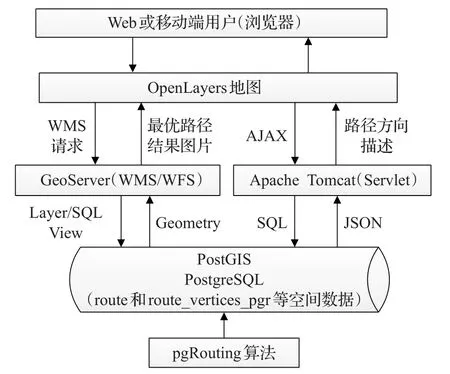
图7 室内外一体化最优路径分析系统实现流程

用户通过Web浏览器访问OpenLayers地图服务，然后与地图交互确定路径分析的起点和目标点坐标，再由OpenLayers请求GeoServer服务器上的路径分析WMS服务。此时，GeoServer在后台调用本文扩展的pgr_fromAtoB函数查询满足条件的路径网络数据，最后将查询到的最优路径结果图片返回OpenLayers客户端，对应的路径方面描述信息则利用相关SQL语句在PostgreSQL数据库查询，并通过JSON（Java Script Object Notation）数据格式返回客户端进行解析和显示。

在PostgreSQL中实现自定义函数pgr_fromAtoB的核心SQL语句为：SELECT gid，name，geom，a.cost，a.source，a.target FROM pgr_dijkstra（‘SELECT gid as id，source，target，length AS cost FROM route’，source，target，false，false） a，route WHERE id2=gid ORDER BY seq。该查询将pgr_dijkstra得到的初级结果与原始线路表进行关联，可以获取结果线路上更多属性信息，便于路径方向语义信息获取。在此基础上，利用GeoServer配置路径查询WMS服务的关键SQL语句为：SELECT ST_MakeLine（route.geom） FROM（SELECTgeom FROM pgr_fromAtoB（‘route’，%x1%，%y1%，%x2%，%y2%，%queryType%）ORDER BY seq）AS route。将客户端请求的起止点坐标和查询类型作为GeoServer WMS服务请求参数，即可计算出最优路径，并返回线路结果几何对象。路径方向描述则利用Java Servlet这种数据库和应用程序之间的中间层实现，部署在Tomcat服务器下，并在OpenLayers客户端利用AJAX（Asynchronous JavaScript and XML）技术来实时获得方向描述语义信息。

4.2 实验数据描述

采用天津市主城区的道路网络及部分建筑室内路径数据作为测试数据，其中，城市道路交通网络数据从OpenStreetMap开源网站下载，利用开源工具osm2pgsql将其导入PostgreSQL；两幢建筑物的室内几何网络模型数据基于各楼层平面设计图（AutoCAD数据）在ArcGIS 10.2软件中制作而成，并利用PostGIS 2.0提供的ShapeFile and DBF Loader Exporter工具将其导入PostgreSQL。第1幢建筑共5层，包含3部电梯和3座楼梯；另一幢3层建筑包含2部电梯和2座楼梯。在PostgreSQL中构建拓扑关系后的几何网络模型共包含32 906条边和30 019个节点。其中，室外道路32 234条，室内路径672条。

除了道路线要素和对应的节点外，为了能够直观展示楼宇内部结构，本文将连通室内路径的房门、楼梯出入口、电梯出入口、紧急通道出口等兴趣点数据（poi）、室内房间布局轮廓线数据（room_line）、建筑物轮廓（building_polygon）等辅助矢量数据也一并导入PostgreSQL，并通过GeoServer发布图层服务。两幢建筑室内空间数据及部分室外连通路径的空间分布如图8所示。

4.3 实验结果及分析

利用本系统提供的坐标点选择工具从室外道路上选择一个点作为起始点（五角星标识），再从某幢建筑的二楼走廊上选择一个目标点，按照“距离最短”方式进行查询，其结果如图9所示（红色加粗折线标识）。

图8 室内外一体化道路网络模型数据示例

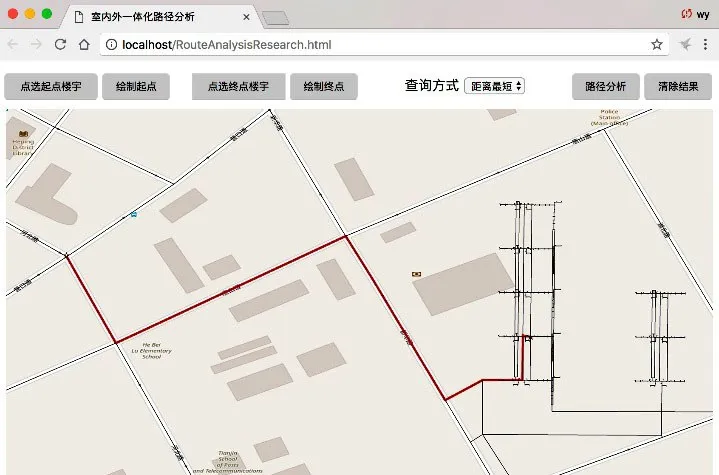
图9 室内外一体化路径分析结果展示

图10 室内外一体化路径分析结果展示

接下来分别从两幢建筑的2楼走廊选取一个点作为起始点和目标点，按照“时间最少”方式进行查询，其结果如图10所示，地图右上方显示详细的路径方向描述信息。由于乘坐电梯的时间成本比楼梯步行成本要小，因此算法会优先选择乘坐电梯上下楼。针对起止点都在室内的查询，本文采用3种方式优化查询结果地图展示：（1）当起点和终点在同一楼宇的同一楼层时，系统只显示该楼层的平面布局图并标识结果路径；（2）当起点和终点在同一楼宇的不同楼层时，系统只显示该楼宇这些楼层之间的整合图并标识结果路径；（3）当起点和终点位于不同楼宇内部时，系统默认展示这两栋楼宇的室内整合图和室外连接路径部分。此外，系统还提供“室外路径”、“起点室内路径”和“终点室内路径”等选项，可分别展示路径结果的不同细节。

为了验证最优路径分析结果的正确性，将该实验数据以及与图10相同的起止点在ArcGIS 10.2桌面软件ArcMap中进行路径分析（设置网络阻抗为Length字段），所得结果如图11所示。可以看出，本文结果与ArcGIS软件计算结果完全一致。选择任意的起止点进行大量的对比测试，发现结果均相同，说明本方法计算结果可靠。

图11 ArcGIS最优路径分析结果

实验所用台式计算机配置为Intel®CoreTMi7-6700 CPU@3.4 GHz双核，16 GB内存，Windows 10 64位操作系统，选择5组代表室内外不同道路上的点作为输入，分别对应于5组不同的室内外一体化路径分析结果规模（路径边数量等），以线路长度作为网络成本，测试算法的执行效率，所得结果见表3。5组查询结果耗时均在60 ms以内，平均耗时为50.4 ms，并且查询效率与结果路径边数量和总长度关系不大。

表3 不同查询规模的效率对比

本文使用的Dijkstra算法也与pgRouting库内置的其他最短路径分析算法进行了效率对比。由于Johnson和Floyd-Warshall是全源最短路径算法，使用全部测试数据耗时非常长，因此仅选取包含图8所示的部分路径（679条边）作为测试数据。针对Dijkstra和A*算法，起始点与目标点对应的source=30，target=238，4种算法结果见表4。

表4 不同最短路径算法效率对比

可以看出，在单源最短路径方面，A*算法比Dijkstra算法效率高，因为A*算法采用启发式搜索，通过估价函数进行有选择的遍历，优于Dijkstra算法的盲目搜索。但是，在大量测试过程中，选择某些起止点，使用Dijkstra算法能求解出最短路径，而A*算法无查询结果，不能保证获得最优解。Floyd-Warshall和Johnson这两种算法[23]需要计算所有节点之间的全源最短路径矩阵，效率非常低，因为Floyd-Warshall算法时间复杂度是O(|V|3)，Johnson算法时间复杂度为O(|E||V|+|V|2lg|V|)。并且随着V和E元素的增多，这两种算法与Dijkstra算法的效率差别会更加明显。

5 结束语

本文提出了一种能够兼容Dijkstra等成熟路径分析算法的室内外一体化几何网络路径模型，在该模型中设计了一种楼层坐标偏移策略，既能满足室内垂直方向网络拓扑关系的构建，又能实现三维空间下的室内多层路网数据二维可视化表达。对开源pgRouting库提供的高效Dijkstra算法进行扩展，能快速查找出离输入点最近的线路节点，从而实现任意两点间最短或最快路径查询，并返回结果路径的空间位置和转弯方向语义描述信息。使用大规模室内外一体化道路网络数据在开发的原型系统中进行实验，经大量测试均能快速准确查询出两点间最优路径结。本文提出的室内外一体化道路网络数据模型和基于开源软件的最优路径分析解决方案具有普适性，能够满足室外、室内、室内外一体化等多种环境下的最优路径分析，方法简单高效，通用性强。今后拟考虑室外汽车行驶速度、道路拥堵程度等多种网络成本，并实现动态最优路径规划，更好地满足公众的室内外一体化路径导航需求。