贝塞尔曲线插值下的聚焦形貌恢复

张 明 ，丁 华 ，刘建成

（1.太原理工大学 机械工程学院，山西 太原 030024；2.School of Engineering and Computer Science，University of the Pacific，Stockton，CA，95211，United States）

1 引言

为提升聚焦形貌恢复精度，国内外学者进行了广泛深入的研究，主要涉及到利用曲线拟合插值法对初始深度图做近似处理。文献[1]运用改进的拉普拉斯聚焦算子对聚焦评价函数曲线峰值附近的三个数据点进行高斯插值，获得了较为精确的深度信息。文献[2]通过寻找理想聚焦表面（FIS）的斜面近似，提出一种全新的聚焦形貌法—SFF.FIS（focus image surface）。为了处理复杂表面形貌，文献[3]采用二阶拉格朗日多项式插值法获得一个三次曲面，并用此曲面逼近理想聚焦表面（FIS）。文献[4-5]提出一种基于离散差分预测模型算法提高了恢复精度。文献的代表性研究有：在离散余弦变换域中应用PCA（主成分分析）计算聚焦评价值；采用三次贝塞尔-伯因斯坦多项式对初始深度图数据进行拟合[6]；借助遗传算法实现深度值的优化组合[7]，这些方法均实现了精确的三维形貌恢复。上述部分研究在形貌恢复精度提升方面取得了较为理想的结果，但其实现的前提是要假定聚焦评价函数曲线遵循某种特定分布模型，因而具有一定的局限性。

为获取更为精确，完整的深度值信息，在分析了序列图像噪声类型的基础上，对图像进行中值滤波预处理，减少了噪声干扰；结合近似处理手段，对由聚焦评价函数获取的初始深度值进行三次贝塞尔曲线插值处理，获取插值后函数的最大值位置作为特性曲线的峰值位置，进而确定景物深度，恢复其三维形貌。实验结果表明，该方法不仅提升了峰值定位精度，而且实现了深度值的精确估计。

2 聚焦形貌恢复原理

聚焦形貌恢复技术就是要从部分聚焦的图像序列中提取图像的高频成分，重构物体的全聚焦图像和恢复3D形貌（深度图）[8]。其原理，如图1所示。其基本思想[9]是：首先，通过调整显微镜z轴位置，获取显微样本的序列图像，使整个序列覆盖在显微镜中的全部z轴方向的高度信息，每幅图像有聚焦清晰区域和模糊区域；然后在序列图像中通过一定的叠合规则，获取每个像素点所对应的聚焦清晰位置，从而重建出一副十分清晰的图像，再通过聚焦分析，恢复深度信息；最后对深度信息进行插值拟合，恢复出比较精确的物体深度信息，从而通过二维图像序列进行三维重建和测量。

图1 聚焦形貌恢复原理图Fig.1 Schematic Diagram of Shape From Focus

聚焦评价函数作为表征图像清晰度的尺度，其在聚焦形貌恢复中扮演着至关重要的角色，其最大值点对应着正确聚焦，即图像最清晰的时刻。主流的聚焦评价函数有SML（改进的拉普拉斯算子），Tenengrad函数，以及GLV（灰度方差函数）等。

3 中值滤波除噪

图像噪声的存在大大影响了初始深度值估计的精确性。消除噪声干扰的主要手段是采用滤波的方法，为了获取更好的滤波效果，首先必须对图像噪声类型有一个准确的初步判断，进而根据噪声类型选择合适的滤波方法。针对目前噪声类型估计困难的问题，文献[10]从直方图信息灰色关联的角度出发，总结了常见含噪图像（高斯噪声、椒盐噪声以及斑点噪声）均匀区域内灰度直方图分布特征：含高斯噪声灰度均匀区域直方图分布特性近似于高斯分布；含椒盐噪声灰度均匀区域直方图有三个波峰，分别对应原始灰度、纯黑和纯白；含斑点噪声灰度均匀区域直方图分布近似于均匀分布。

依据上述理论，我们对采集到的序列图像进行灰度直方图显示，根据灰度图像的直方图分布特征，推断出采集的序列图像的主要噪声类型为椒盐噪声，而中值滤波非常适合去除椒盐噪声，且在去噪的同时能够很好地保持图像边缘信息。因此，我们选择中值滤波对序列图像进行预处理。

4 基于贝塞尔曲线插值的聚焦形貌恢复

4.1 贝赛尔曲线

贝塞尔-伯因斯坦多项式广泛应用于计算机图像学、特征提取、图像分割、数据近似等领域。其一般数学表达式为：

式中：p—多项式阶数；t—定义在［0，1］上的多项式参数；Fi—贝塞尔曲线的控制点；Φip（t）—p阶伯因斯坦基底多项式。当p=3时，我们称作三次贝赛尔曲线，其参数和矩阵形式分别为：

针对上述问题，我国银行和中小企业都需要提升业务人员的综合素质，银行和中小企业可以通过培训的方式，促使业务人员掌握国际金融市场的法律和知识，尤其是贸易和融资方面的知识，例如：国际金融商场的主要金融产品及其金融产品的性质和特点。银行和中小企业在培训业务人员理论知识的同时，也要注重实际操作能力的培训，并在培训过程中及时吸取培训经验，不断补充和完善培训计划，以此来提升业务人员的专业水平。此外，工作人员自身也要积极学习，提高自身的分析能力，及时把握金融市场的动态，了解国际金融市场的变化，准确地对风险进行预测，继而增强中小企业在国际金融动荡环境下的风险抵御能力。

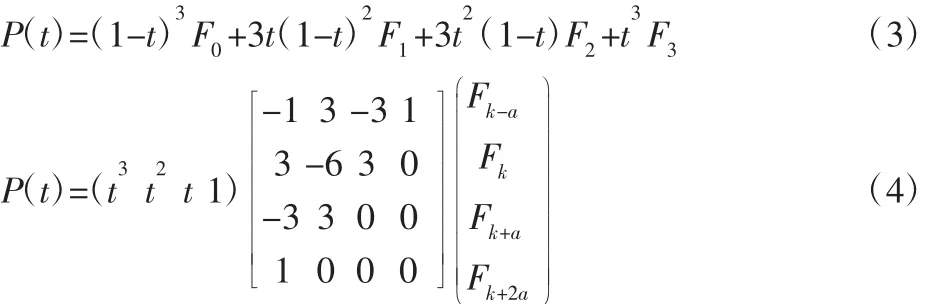
贝塞尔曲线插值的关键在于控制点，多项式曲线参数a以及输入曲线数据点的选择[6]。为了获取更为精确的深度值信息，我们利用三次贝塞尔曲线对初始深度矩D（x，y，k*）进行插值处理。由于插值曲线只是在峰值两侧的一定范围内和评价函数特性曲线相似，所以聚焦评价函数特性曲线半宽越小，选取的插值点数应该越少。通常情况下，选取评价函数曲线峰值两侧的（6～8）个点就可得到满意的深度恢复精度。当我们取a=2时便可得到7个数据点，（Fk-2，Fk-1，Fk，Fk+1，Fk+2，Fk+3，Fk+4）以及 4 个控制点（Fk-2，Fk，Fk+2，Fk+4）。这里 k 为像素点（x，y）聚焦评价曲线峰值位置对应的图像序号（深度），Fi为相应的聚焦评价值；根据这些输入曲线数据点和控制点，我们即可确定三次贝塞尔插值曲线，并将其最大值位置对应的m=argtmax（P（x））作为精确处理后像素点（i，j）的深度，对所有像素点执行这样的操作便可获取新的深度矩阵D′（i，j，m）。

考虑金属圆盘序列图像经中值滤波后像素点（200，200）的SML聚焦评价特性曲线，该像素点处的初始深度值为50。取a=2时，三次贝塞尔曲线插值所需的原始曲线由7个数据点（F48，F49，F50，F51，F52，F53，F54）构成，4个控制点分别为（F48，F50，F52，F54），根据这些输入点及控制点得到的插值结果，如图2所示。可知插值后该像素点的深度值为50.36，相比于初始深度值50更为精确可靠。

图2 三次贝赛尔曲线插值Fig.2 Three Degree Bezier Curve Interpolation

4.2 聚焦形貌恢复算法描述

根据上述理论设计聚焦形貌恢复算法，具体步骤如下：

Step 1：利用中值滤波对序列图像进行预处理以减少噪声对恢复精度的干扰。

Step 2：应用聚焦评价函数计算序列图像每个像素点（i，j）的聚焦评价值。

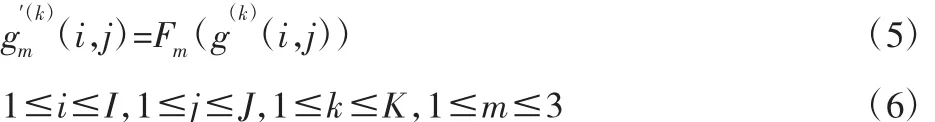
式中：I，J—序列图像的行数和列数；K—序列图像总数量；m—所

用聚焦算子序号。

Step 3：获取初始深度值：将 Step 2 得到的每个像素点（i，j）在序列图像中的聚焦评价值进行比较，并找到最大评价值对应的图像序号，从而获得初始深度值。

Step 4：根据Step 3得到的初始深度值确定贝塞尔插值所需输入曲线及控制点。

Step 5：贝赛尔曲线插值：利用三次贝赛尔曲线对初始深度值进行插值处理。

Step 6：将插值后曲线的最大值位置作为特性曲线的峰值位置，得到更为精确的像素点（i，j）的深度值：

Step 7：根据所有像素点的最终深度值重构三维形貌。

5 实验与分析

实验所需数字图像由型号为Basler Ace acA645-100um monochrome的CCD摄像机（图像分辨率为659*494）采集，计算机配置：CPU为2.53GHz，内存2GB。基于Windows平台，实验的算法应用VC实现。首先，利用夹具将实验对象固定起来，然后将摄像机固定在机床探臂上。摄像机调节步长为10μm，通过控制机床探臂的伸缩可调节摄像机Z轴方向高度，使摄像机的成像面聚焦在不同高度层面，顺序采集100帧659*494大小的图像，经USB3.0数据线传至计算机。形貌恢复实验中的参考算法选择为FGLV、FSML、FTEN等传统聚焦算子，实验对象选用不同材质的表面细节特征丰富的3D打印实体和金属圆盘，以验证方法在形貌恢复精度方面的高精度性以及有效性。考虑到计算量及评价窗口尺寸对恢复精度的影响，计算窗口大小选择为（3×3）。恢复算法简写为FBBP。实验装置及实验对象，如图3所示。

图3 实验装置及实验对象Fig.3 Experiment Setup and Objects

参考算法FSML、FTEN、FGLV以及这里的FBBP方法所获取的3D打印实体和金属圆盘的三维形貌图，如图4所示。定性分析，不论对3D打印实体还是金属圆盘，基于梯度二阶差分的FSML算子恢复得到的三维形貌都出现了一定程度上的缺失，尤其在3D打印实体凹槽及金属圆盘中心处丢失了过多图像信息，此外金属圆盘边缘凹凸不平，平整性较差。相比于FSML，FTEN、FGLV恢复得到的3D打印实体形貌图有所改善，整体形貌细节部分均已基本显示出来，平整性也较好，而且两者形貌恢复结果差异性较小。FTEN、FGLV获取的金属圆盘形貌图在边缘细节处重建效果有了大幅改善，图像整体轮廓也都基本重建出来，只是FTEN在中心圆环处出现了凸起，小部分边缘形貌信息有所丢失。而FGLV不论在边缘还是中心处都显得很是平整，整体恢复效果明显。显而易见，相比于其他三种方法，这里方法获得的3D打印实体三维形貌更加完整可观、清晰可见，且光滑平整，尤其在凹槽、圆坑等表面细节处更为突出。由于金属圆盘的反射性能较强，再加上其表面光滑，细节纹理丰富，因而其他三种方法均会出现不同程度上的形貌缺失问题，且表面粗糙度较大，而这里方法获得的三维形貌更为完整，平滑，真实可观性也大大提高。总体上看，重建出来的三维形貌图较其他传统方法而言，纹理信息保持较好，边缘细节清晰可见，重建结果整体性较好。为了定量评价恢复效果，利用评估准则RMSE（均方根误差）及Correlation（相关度）对四种方法恢复效果进行了对比。这里，RMSE值越小，Correlation值越大表明估计的深度值与实际深度值间的误差越小。

图4 3D打印实体形貌金属圆盘形貌Fig.4 3D Shapes Reconstructed for 3D Printed and Metal Disk

统计了四种恢复方法下3D打印实体和金属圆盘聚焦形貌恢复效果评价数据，如表1所示。从RMSE一栏可知，无论何种实验对象，FSML对应的RMSE值最大，FTEN及FGLV的RMSE值较为接近，FBBP对应的RMSE指标最优；Correlation一栏显示，FSML对应的Correlation值最小，FBBP对应的Correlation值最大，分别达到了0.9453、0.9208，这些数据充分表明FSML的形貌恢复误差最大，而FBBP法恢复效果最优（估计深度值与实际深度值近似程度最高）。通过定性与定量分析可知，提出的方法较传统方法在恢复精度方面具有一定的的优越性。

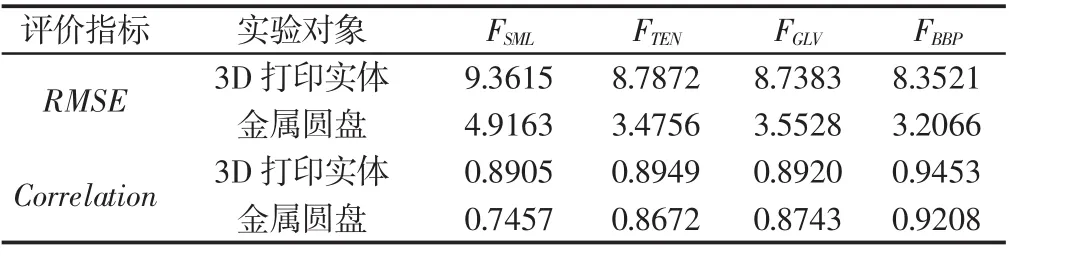
表1 3D打印实体和金属圆盘聚焦形貌恢复效果评价Tab.1 Recovery Effects Evaluation of 3D Printed and Metal Disk

6 结论

在对图像噪声类型识别理论及近似技术的研究基础上，实现了一种高精度的聚焦形貌恢复方法。为了有效消除噪声干扰，从含噪图像灰度直方图分布特性入手，经过噪声类型初步判断后采用中值滤波对序列图像进行预处理；引入三次贝赛尔曲线插值法对初始深度图作近似处理，从而获取更为精确的深度值信息。为了对恢复效果进行定性与定量分析，分别选用不同表面特征与材质的实体对象（3D打印实体和金属圆盘）进行形貌恢复实验，并将FSML、FTEN及FGLV算子作为参考算法。结果表明，提出方法的RMSE、Correlation指标均优于FSML、FTEN及FGLV，恢复精度分别达到了94.53%，92.08%，充分说明该方法兼具形貌恢复的高精度性与普适性。