二元驱动串并联机器人结构参数约束条件分析

杜幸运，赵 慧，徐鹏成

（武汉科技大学 机械自动化学院，湖北 武汉 430081）

1 引言

随着工业技术的发展，人们希望能够用最少的输入来产生较多维数空间运动的机械结构，使机器结构简单、制造容易、高效可靠、维修方便、节能减排的目的[1]，因此研究新型机构将成为实现这一目标的良好途径。二元驱动器（binary actuators）是驱动器中的特殊一类，只具有两个离散的稳定状态，标记为0和1，分别对应于驱动器的两个极限位置。和传统的机器人系统相比，二元驱动串并联机器人不需要反馈控制、成本低、且具有高负载能力、定位和重复定位精度高、鲁棒性强等优点，但其缺点是工作空间不连续，很难求逆解。

国际上对二元驱动串并联机器人离散系统研究较为有影响力的团队分别是JHUChirikjian团队和MITDubowsky团队。文献[2]提出了一种基于齐次变换的运动学正解计算方法，研究了二元驱动串并联机器人平面变几何珩架机构（VGT）正运动学求解算法并验证了算法的有效性。同时，文献[3]通过改变二元驱动器驱动腿变化量，研究了其对工作空间的影响，并提出了用于二元驱动串并联机器人拾取任务的优化算法。文献[4]研究二元驱动串-并联机器人离散系统参数综合问题。提出了二元机器人驱动智能装置BRAID（Binary Robotic Articulated Intelligent Device）的概念，并进行了大量相关理论和实验技术研究，文献[5]对基于BRAID的二元驱动串-并联机器人系统的结构设计、驱动器及控制、运动学等做了研究。文献[6-7]研究了使用介质聚合物二元驱动器的BRAID的运动学以及驱动器优化。文献[8]分别研究二元驱动串-并联机器人平面（2-D）和空间（3-D）的正运动学问题并提出基于连续变量优化方法的运动学反解方法。JHU Chirikjian团队和MIT Dubowsky团队的研究工作重点放在对其末端位置空间的研究，其姿态问题很少考虑，尤其是二元驱动串并联机器人末端姿态与结构参数的关系更未考虑。文献[9]研究了空间并联机器人末端动平台位置空间和姿态欧拉角，但并没有定量的给出驱动腿变化量与结构参数变化关系，因为此关系对机器人末端姿态欧拉角存在与否有重要的影响。在一个二元驱动的离散系统中，工作空间由一系列离散点组成，因此分析离散系统的工作空间即为分析空间内工作点的分布云图，文献[10]分析得出结构参数对系统工作空间点分布范围及系统的精度具有明显的影响，但是并没有考虑驱动腿与结构参数取值关系影响末端姿态欧拉角的存在，也未考虑驱动腿变化量与结构参数之间的定量关系。

以平面变几何桁架机构（VGT）作为二元驱动串并联机器人基本模块，研究其正运动学并分析其不同驱动腿变化量对末端位置空间的影响。进一步的研究了不同结构参数对末端姿态的影响，根据上、下平台之间相对姿态转角为实数的约束条件，用MATLAB语言编写正运动学计算公式，求出末端动平台姿态转角，对结构参数和驱动腿变化量进行大量的取值计算，得出不同驱动腿变化量对应不同的结构参数的取值范围。因此得出结论：结构参数的合理取值，可以避免因为结构参数的选取不当，无法求得相应的姿态欧拉角，另外，在执行精度较高的任务场合时，不仅可以通过控制机器人驱动腿变化量来改变末端姿态，还可以同时通过控制改变结构参数值实现机器人末端位姿的变化。

2 VGT正向运动学分析

二元驱动串并联机构，如图1所示。共有5个完全相同的模块组成，且末端执行器位于最高一级模块平台中心处。其中每个单元模块有三条腿，每条腿由气动驱动，只有两个稳定状态。这样，3条驱动腿，可以实现8种构型，因此，末端执行器所能达到的空间位置将随模块串联数的增加而呈指数增长。五级二元驱动串并联机器人可以达到的空间位置点数为85，如图1所示。

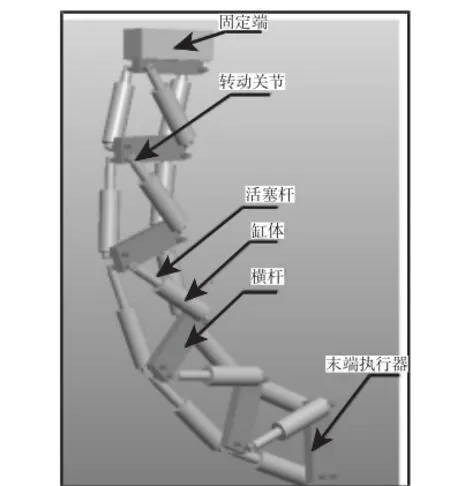
图1 五级二元驱动串并联机器人Pro/E三维结构简图Fig.1 Five-Stage Binary Actuators Series-Parallel Robot of Pro/E Three-Dimensional Structure Diagram

根据机器人机构学的知识，机器人正向运动学表示各关节参数q和结构参数w与机器人末端执行器空间位置的关系[3]，因此机器人的正运动方程可以表示：

式中：x—末端的位置和姿态矢量；w—结构参数，它是根据机器人结构的不同而异，如图2所示。结构参数为除了驱动腿之外的所有杆件的宽度为w，且w∈—关节参数。

对于N个基本模块串联一起构成的二元驱动串并联机器人离散系统，第i级的关节参数只有两个状态qmin、qmax。按照逆时针方向分别标注 3 条驱动腿为 qi，1、qi，2、qi，3，将笛卡尔坐标系原点置于底部杆件中心点处。

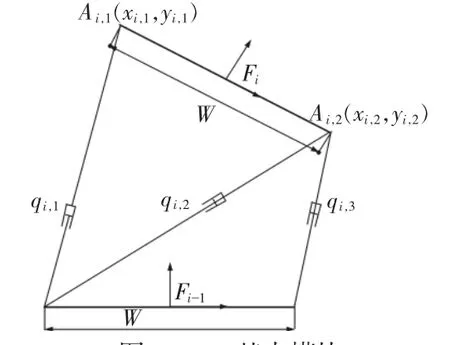
图2 VGT基本模块Fig.2 VGT Basic Module

离散系统的关节参数是一组离散变量，它的取值是一定数值的集合，该集合表示为qi∈ ｛qmin，qmax｝∈R，因此，对任意关节参数可用公式表示为：

式中：B—数字‘0’和‘1’的集合，B∈｛0，1｝；bi∈B，它表示 B 的子集。

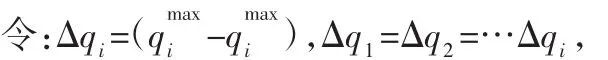
由图 2 可知，已知每个模块驱动腿长 qi∈｛qi，1，qi，2，qi，3｝和结构参数，我们的目标是求两个坐标点 Ai，1（xi，1，yi，1）和 Ai，2（xi，2，yi，2）与驱动腿长之间的方程关系，然后找出上平台中心点相对于下平台中心点之间的几何关系方程式。通过几何关系我们可以求得：

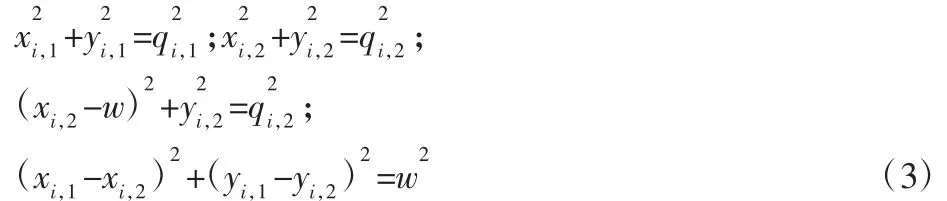
将方程（3）通过MATLAB编写程序求解并简化可得：

第i节机构相对于第i-1节的姿态转角可以表示为：

那么串联ith平台中心点相对基坐标系中心点的绝对姿态转角可表示为：

我们使用gi-1，i表示Fi相对Fi-1，i机构的齐次变换矩阵：

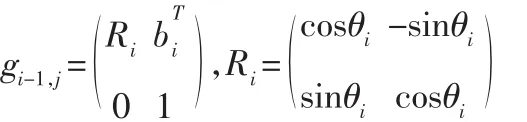
最终，末端执行器平台中心坐标FN相对于基坐标系F0中心可以用gi-1，j表示为[4]：

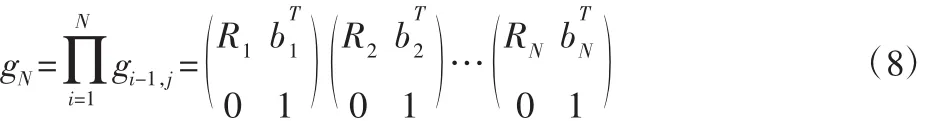
3 二元驱动腿变化量与结构参数分析

根据式（6）编写MATLAB程序求解图2单个VGT基本模块的姿态转角Δθ。当已知驱动腿变化量Δq时，结构参数在一定范围内取值，根据平面变几何桁架结构几何关系，在工程实际中姿态转角属于实数，即Δθ∈R。根据这一约束条件，当已知二元驱动腿qmin和qmax，改变结构参数的值，求取不同的姿态转角，如果计算出的Δθ值属于实数，说明w值可取，如果计算出的值属于复数，w则不可取。进一步的研究驱动腿变化量与结构参数范围的关系，分别取不同的Δq值，通过编写MATLAB计算并记录结果，如表1所示。由于数据太多，只截取四组实验其中一部分数据。通过表 1（单位为 Cm，i∈［1，…，n］，j=1，2，3）中四组数据，可以发现，结构参数的取值范围与驱动腿变化量之间有着密切的关系，即：wmin=Δq=qmax-qmin，wmax=2×qmin。在该机构实际应用中，可以根据驱动腿变化量的不同取值，确定机器人结构参数取值范围，根据这一范围合理取值，可以避免因为结构参数的选取不当，无法求得相应的姿态转角。

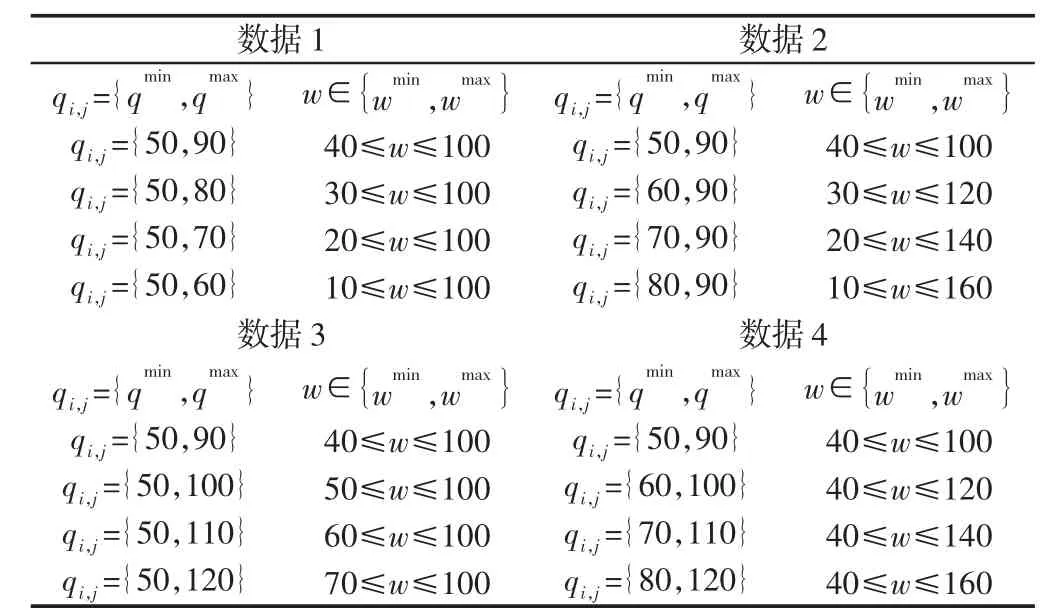
表1 二元驱动腿变化量与结构参数关系Tab.1 Binary Actuators Stroke of Variation Relationship with Structural Parameters

4 工作空间分析

为了分析该五级二元驱动串并联机器人末端执行器的位置空间和姿态变化范围，由式（8）编写MATLAB程序，可求得图1末端执行器的位置空间，如图3所示。以表1中的数据1为例，当结构参数 w=50 时，取驱动腿四组不同值（qi，j=［50，90］，qi，j=［50，80］，qi，j=［50，70］，qi，j=［50，60］），从而改变不同的驱动腿变化量，得出五级二元驱动串并联机器人末端不同的离散点位置分布云图。根据式（7），分析图1末端执行器的姿态，如图4所示。以表1中的数据1为例，当结构参数w=50时，取驱动腿四组不同值（同上），从而改变不同的驱动腿变化量，可得末端平台相对基坐标系的绝对姿态转角的分布云图。为了进一步的说明结构参数对图1末端执行器的姿态的影响，如图5所示。当驱动腿变化量取固定值 qi，j=［50，70］时，取四组不同的结构参数（w=100，w=70，w=40，w=20），可得末端平台相对基坐标系的绝对姿态转角的分布云图。从图3和图4中可以得出：当结构参数固定时，末端执行器的位置空间和姿态空间随着驱动腿变化量的减少而减少。从图5中可以得出：当驱动腿变化量固定时，末端执行器的姿态空间大小随着结构参数的减少而增大，然而末端执行器的姿态区间的离散点的密度随着结构参数的减少而降低。如果该机构应用在精密仪器中，可以通过合理增加结构参数的值使其在姿态区间的离散点的密度增大，从而提高五级二元驱动串并联机器人作业任务的精度。

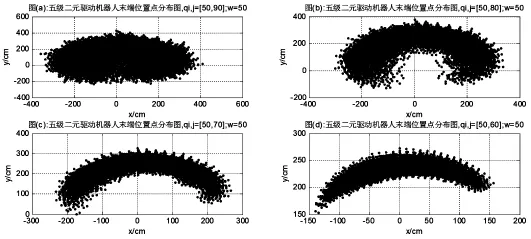
图3 五级二元驱动机器人末端位置点分布云图Fig.3 Five-Stage Binary Actuators Robot End Location Map

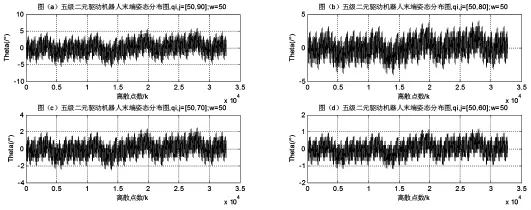
图4 五级二元驱动机器人末端姿态分布云图Fig.4 Five-StageBinary Actuators Robot End Posture Map

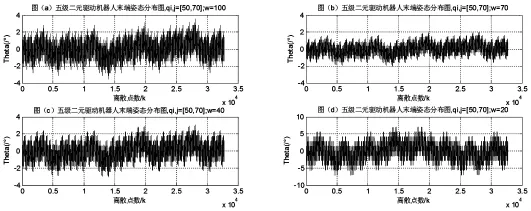
图5 五级二元驱动机器人末端姿态分布云图Fig.5 Five-StageBinary Actuators Robot End Posture Map

5 结论

研究平面变几何珩架机构的正运动学及驱动腿变化量和结构参数对其工作位置空间和末端位姿的影响，通过改变驱动腿变化量和结构参数的取值，验证了不同参数对末端工作空间的影响。在工程实际中，姿态转角属于实数这一约束条件，研究驱动腿变化量与结构参数取值范围的关系，经大量计算得出；（1）结构参数最小值等于驱动腿两个极限位置之差的绝对值，结构参数最大值等于驱动腿极限最小值的两倍。该结论解决了驱动腿变化量与结构参数的取值问题，定量的分析了其两者之间的关系，从而可以避免因结构参数盲目取值而无法求得姿态角的问题。通过对其工作空间的分析，从图3和图4中可以得出；（2）当结构参数固定时，末端执行器的位置空间和姿态空间随着驱动腿变化量的减少而减少。从图5中可以得出；（3）当驱动腿变化量固定时，末端执行器的姿态空间大小随着结构参数的减少而增大，然而末端执行器的姿态区间的离散点的密度随着结构参数的减少而降低。如果该机构应用在精密仪器中，可以通过合理增加结构参数的值使其在姿态区间的离散点的密度增大，从而提高五级二元驱动串并联器人作业任务的精度。以后的研究将会考虑空间串并联机器人，研究驱动腿与结构参数的关系，平面变几何珩架机构的驱动腿变化量与结构参数的关系是否也适用于空间并联机器人结构设计与优化有待进一步的研究，另外，系统的动力学特性，尤其是并联机构中的转动关节和气缸受力情况也是将来研究的一个方面。