滚动轴承全寿命数据监测分析及特征提取

芮晓明，胡鑫

(华北电力大学 能源动力与机械工程学院，北京 102206)

0 引言

机械、运载、能源、冶金、电力等国民经济行业中的设备往往处于高负荷、变载荷和持续的运行状态，设备核心机械部件和结构不可避免地会发生劣化和失效，造成很大的经济损失、资源浪费、环境破坏，甚至人员的伤亡。因此，设备安全可靠性非常重要。

滚动轴承作为机械设备的基础性零件，在旋转机械中有着广泛的应用。据统计，将近一半的旋转机械故障是滚动轴承的损坏所造成的，其主要原因在于滚动轴承的工作环境一般相对恶劣，并且有时零件的加工和安装工艺不好，或轴承维护条件欠佳，或突然的冲击载荷会使轴承运行一段时间后产生各种各样的缺陷，而继续运行一段时间后，缺陷会进一步扩展，轴承逐渐劣化甚至失效[1-3]。

目前，轴承故障监测的很多方法对操作人员的经验有很大的依赖性，且容易误报和报错，局限性比较大。当然也有很多学者提出了小波分析、能量分析、包络分析、KPCA和WPHM等数据监测方法[4-6]，这些方法对轴承的故障监测有一定的作用。

滚动轴承常见的失效形式有疲劳点蚀、磨损、塑性变形、腐蚀、断裂和胶合[7-10]，这些故障能引起振动信号的变化，本文则利用matlab对振动信号的时域特征值、频域能量特征值和倒频谱能量特征值进行处理分析，达到对轴承故障进行比较可靠的数据监测和寿命预测的目的，这对提高关键设备的可靠性、经济性和安全性有着至关重要的作用。

1 理论基础

1.1 时域分析法

以时间作为参照来观察分析振动信号的方法称为时域分析。时域波形反映了许多振动信号特征的信息，包括信号类型、幅度范围、简谐成分、周期成分或脉冲成分、故障引起的瞬时脉冲成分、共振、拍频和调制等。时域分析方法是一种经典的信号处理方法，一直是状态监测和故障诊断的简单且有效的方法。

本次通过提取时域的一些时域特征值对数据进一步分析。

1.2 频域分析法

随着故障的发生、发展，往往引起信号频率结构的变化，通过时域分析有时候很难判断信号中包含了哪些频率成分及其幅值和相位，但如果以频率作为参照，将信号中不同频率成分的幅值和初始相位分别在频率周上表示出来，就可以清楚地了解信号中的频率构成情况，从而获得更多的有用信息，这就是频域分析。测试信号的频域分析是采用傅里叶变换，将时域信号变换为频域信号，从而帮助人们从另外一个角度对信号进行分析的一种方法，也称频谱分析。频谱分析是振动信号分析的最主要方法，也是现代信号分析方法的基础。

在测试信号中，分模拟信号和数字信号2种类型。在进行频谱分析时，对于模拟信号来说，首先需要对模拟信号进行抽样，使其离散化后进行离散傅里叶变换(DFT)或者快速傅里叶变换(FFT)，然后对其幅度(ABS)和相位(ANGLE)的图像进行分析，而对于数字信号来说，则可直接进行离散傅里叶变换或快速傅里叶变换，傅里叶变换公式如下。

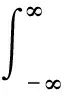
式中：X(f)为频域信息；x(t)为时域信息；f为信号频率；t为时间，s；e为自然常数；j为虚数单位。

1.3 倒频谱分析法

倒频谱是通过对频谱函数再进行傅里叶变换，也可以将频谱中的周期成分表示成单值形式，从而揭示频谱中的周期成分及其变化情况。根据这种思路，Bogert等人于1963年首先提出倒频谱的概念，即对信号自功率谱的对数进行傅里叶变换，得到一个称作倒频谱的新函数。Bogert等人首先提出的是功率倒频谱，随后还有其他不同形式的倒频谱被提出，像功率倒频谱、逆变换倒频谱、幅值倒频谱、复数倒频谱和实倒频谱。

在这5种倒频谱中，实倒频谱目前应用很广泛，由于不考虑相位信息，因此比其他倒频谱的计算方便得多。实倒频谱函数的定义为对数幅值谱的逆变换。

实倒频谱会使信号的幅值得到较大的加权放大，能够使幅值小的成分更加突出。倒频谱分析还有一个优势在于：振动信号特征量会因传递路径受到影响，倒频谱分析对传感器检测点的选取和信号的传递路径不敏感。

2 实验平台及测试系统

本次试验所用的实验台是PRONOSTIA实验台，其中电机功率为250 W，转速为2 830 r/min，使用气压活塞加载。在测试系统方面使用DYTRAN3035B振动加速度，信号采样频率为25 600 Hz，信号的采样长度为0.1 s/10 min。试验采用1个轴承上的2个通道采集数据，这些试验数据描述了滚动轴承从开始测试到轴承劣化的全过程的试验。 如图1所示。

3 信号数据的特征提取

3.1 时域特征值的提取

测出滚动轴承全寿命振动的时域波形图，如图2所示。

通过使用matlab对2个通道的时域信号进行处理，得到滚动轴承全寿命振动变化趋势的时域特征值曲线，如图3所示。

通过对滚动轴承振动信号的时域特征值分析可知，脉冲指标的变化并不明显，即这些指标不能清晰的对滚动轴承的状态进行检测。峭度反映信号中的冲击成分和概率密度函数的陡峭程度，在振动初期对振动信号中包含的冲击成分非常敏感，这一阶段峭度指标值变化非常明显，而之后回落到正常值的范围内，适用于故障早期的局部数据监测。

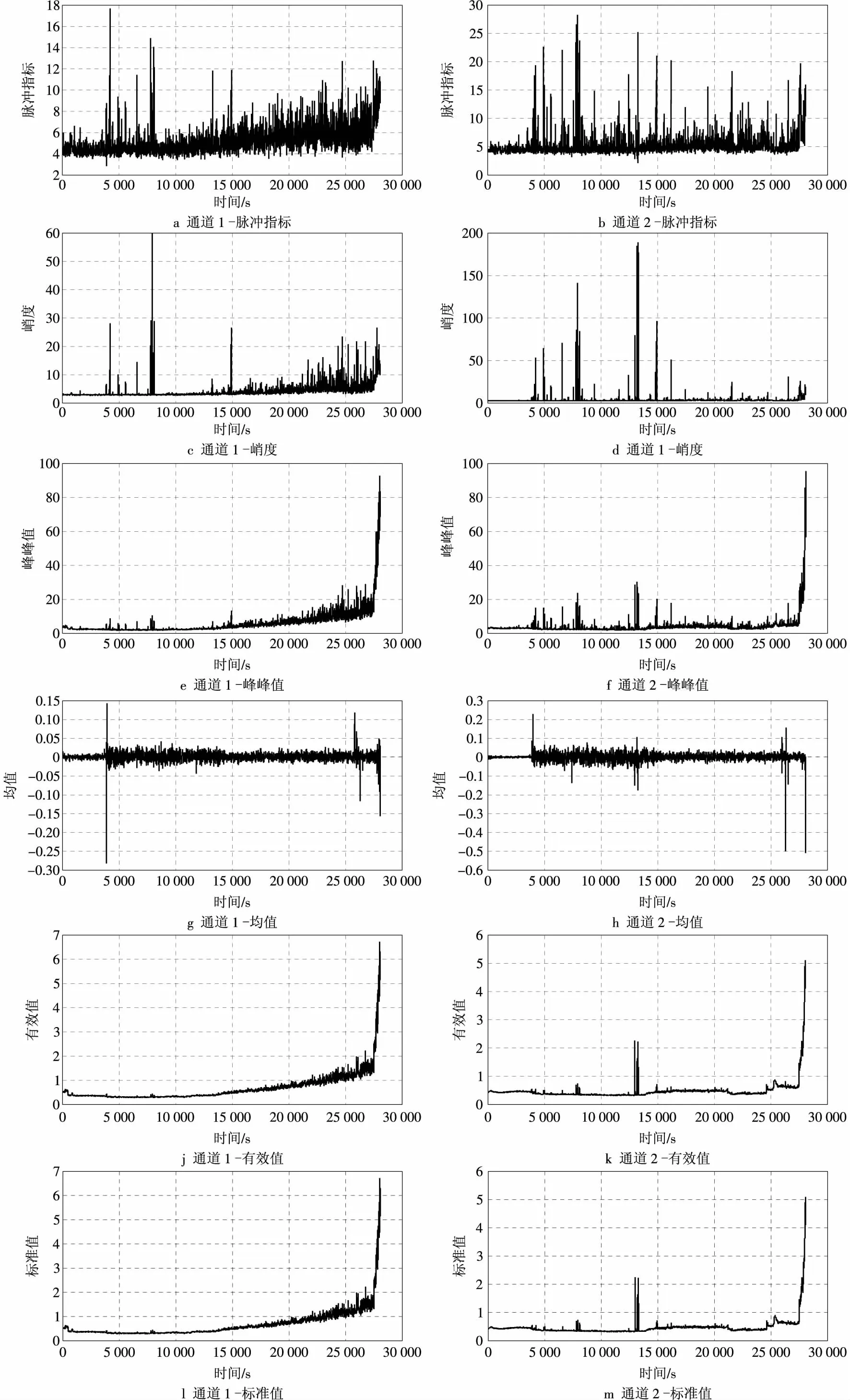
图3 滚动轴承时域特征值趋势

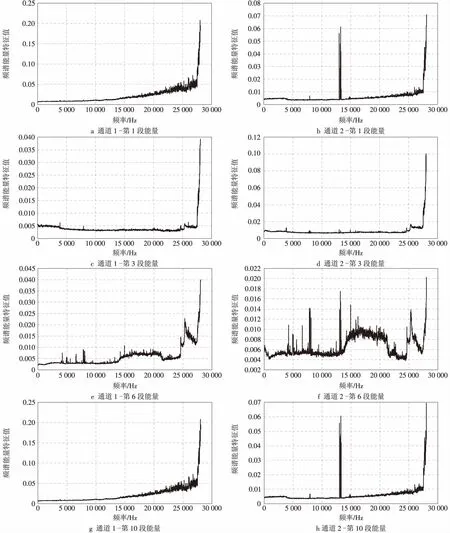
图4 滚动轴承10段频谱能量特征值趋势

峰值反映了信号幅值的变化范围，反映信号的强度，它们不断增大，可知轴承的故障程度不断增大，此时域特征值对轴承的全寿命监测具有一定的意义。均值反映了信号概率密度函数的中心位置，在试验的后期，均值的数值明显变大，表明轴承的劣化也越来越严重。有效值是时域信号的重要特征值，从图3中我们可以了解到轴承劣化的预警信号以及轴承全寿命发展趋势。标准差是信号方差的平方根，反映随机信号的分散情况。从图中可以看出，轴承正常运转过程中，标准差比较稳定，随着轴承劣化程度的加深，标准差变化非常明显，它们适用于监测轴承，它们可以作为故障轴承评判标准的重要指标。因此，在对滚动轴承的时域特征值分析时，将峭度、均值、有效值和标准差等这些特征值配合使用，可以达到故障数据监测和预测的目的。

3.2 频域能量特征值的提取

通过傅里叶变换将时域信号变换到频率域进行分析的频域分析法是振动信号分析的最主要方法，也是许多现代信号分析方法的基础。对数据集使用matlab程序处理得到频域的10段能量特征值趋势曲线，选取其中的一些频段的能量特征值进行分析，如图4所示。

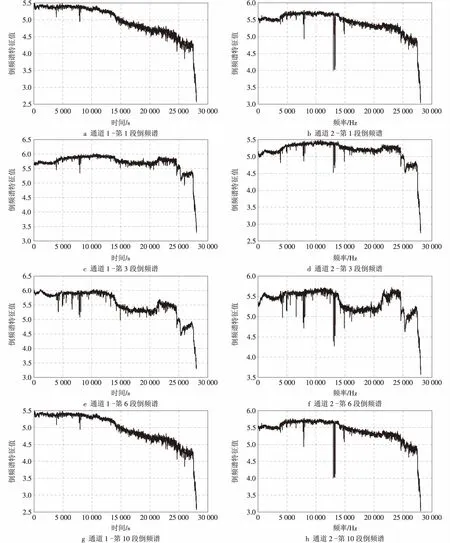
图5 滚动轴承10段倒频谱能量特征值趋势

频谱能量特征值的提取需要首先把时域信号划分成10段信息，其次对其进行傅里叶变换，然后把这些数据集的幅值求均值，最后做出这些频域特征值图线。通过此图线趋势，我们可以更加清晰的了解各个阶段轴承幅值能量的变化情况以及监测轴承发生劣化的全过程。此频域能量特征值更加清晰的表明了整个实验滚动轴承劣化趋势，对工程中滚动轴承的全寿命故障数据监测和寿命预测有很好的作用。

3.3 倒频谱能量特征值的提取

在对滚动轴承进行了时域特征值分析和频域特征值分析后，再次借助matlab对信号处理，利用matlab语言程序很容易实现倒频谱分析，缩短了故障数据监测的时间周期，简化了频谱分析的难度，如图5所示。

倒频谱用于故障监测的基础是其具有从频谱中提取周期成分的能力。在设备运行过程中，如果产生了周期性的冲击激励，则信号就会包含大量的谐波成分，倒频谱就能早期识别信号故障，可以长期跟踪监视滚动轴承的劣化发展趋势。在此基础上，采用类似频谱能量特征值的方法，将数据集分成10段信号进行倒频谱处理，求出其频谱能量特征值的快速傅里叶逆变换，然后对其幅值进行加窗函数处理，再进行一次傅里叶变换，最后求出其幅值的均值，这样就可以得到10段倒频谱的能量特征值。

图中可以更加清晰的了解，到大约进行第14 000次试验采集的时候，滚动轴承开始出现劣化，此后倒频谱幅值缓慢下降，出现一些不稳定的成分：试验进行到大约在进行第25 000次试验采集的时候，图像变化急剧，此时轴承彻底失效。图中前期阶段的倒频谱能量特征值相对变化较小，后期阶段的倒频谱的能量特征值相对前期阶段有很大的不同，尤其在边带成分上更加突出，说明冲击越来越强，轴承的劣化也越来越明显，甚至轴承最后失效。倒频谱特征值相对于时域特征值和频域特征值，对轴承故障数据监测更加清晰，对轴承的寿命预测更加准确和完善。

4 结束语

利用PRONOSTIA实验台对滚动轴承进行全寿命故障试验，并运用matlab对采集到的数据集进行处理，得到振动信号的时域特征值、10段频域能量特征值和10段倒频谱能量特征值，然后根据3类特征值对轴承进行故障数据监测和寿命预测。3种对振动信号的分析方法配合使用，可以大大缩短分析故障的周期，提高生产效率。在经济飞速发展的今天，现代设计制造业对设备的连续性提出了更高的要求，只有对机器零件进行数据监测和寿命预测，才能实现安全生产，提高产业效益。笔者提出的3种对振动信号的分析方法，恰恰满足对设备的数据监测需求，也一定程度上有较大的发展前景。