平面隐式曲线的Hermite插值逼近

魏 利，赵晶洁，黄慧敏



平面隐式曲线的Hermite插值逼近

魏 利，赵晶洁，黄慧敏

(南京师范大学教育信息工程研究所，江苏 南京210097)

隐式曲线在医学图像处理、地理信息系统、数值场可视化等领域中有着重要应用。在分析点采样和曲线逼近理论的基础上，提出一种运用Hermite插值方法逼近平面隐式曲线的算法。首先将曲线绘制区域网格化，在网格单元各边中通过线性插值计算曲线采样点；其次通过计算采样点精简前后构成的曲线段之间产生的误差优化采样点；最后通过Hermite插值法逼近隐函数曲线。实验表明，通过该算法绘制出的曲线在采样点数量较少的情况下，其光滑度和准确度仍较高。

图形绘制；隐式曲线；Hermite插值；采样点优化

隐式曲线是计算机辅助几何设计和计算机图形学的重要研究内容[1-2]，因其可描述平面上任意不规则的形状，且在离散采样曲线重建过程中，具有自动过滤数据噪声的优点，在生物学[3-4]、气象学[5]、地理学[6]、石油勘探及物探[7]等领域有着广泛且重要的应用。

目前，国内外学者主要采用连续跟踪法[2]和细分法[8]绘制隐式曲线。连续跟踪法是从曲线上某一点开始借助一定的规则连续跟踪绘制曲线，如TN法[9]、正负法[10-11]和短线截交法[12]等。这类方法原理简单，容易实现，但其难点在于很难选择一个优化的起始点。细分法是一种常用的隐式曲线绘制方法[13]，该方法首先需要估计其绘制区域，然后排除无关区域，并对有关区域不断细分，直到该区域达到一个像素大小为止，再将其绘制出来。该方法虽能绘制出曲线，但是由于该方法无法优化采样点的分布[14]，因此会生成“胖”曲线[15]。文献[15]对细分法进行了改进，并将自动微分技术与泰勒方法引入其中，该方法可绘制任意复杂的隐式曲线，但其效率(CPU占用时间)有待提升。

绘制平面隐式曲线的方法虽各有不同，但其包含了相同的过程，即获取采样点和曲线折线化。本文参照上述过程并结合已有研究，提出一种新的隐式曲线绘制方法，借鉴移动立方体(marching cubes, MC)方法[16]对绘制区域网格化获取采样点；为减少数据量，提高曲线绘制质量和逼近精度，对采样点数量进行了优化处理；曲线折线化则通过分段Hermite插值实现。实验表明，相比其他隐式曲线绘制方法，本文方法既能减少数据量，同时还可保证曲线准确性和光滑度。

1 Hermite插值

分段三次Hermite插值是函数拟合和插值的基本方法[17]。对于给定+1个插值点0<1…<x和这些插值点上关于函数()的函数值0，1，2，…，y及导数值0，1，…，m，对任意=0，1，2，…，在区间[x，x+1]构造次数不大于3的多项式的分段插值，且有(x)=y和′(x)=m，那么函数()即为插值点(0,0)，(1,1)，…，(x,y)的分段三次Hermite插值函数。

若已知两点01及其切向矢量0′、1′，即可根据两点构成的三次Hermite参数方程求出插值点进而描述点01间的曲线。

为推导出三次Hermite参数方程[18]，首先假设平面上一条三次参数曲线表达式为

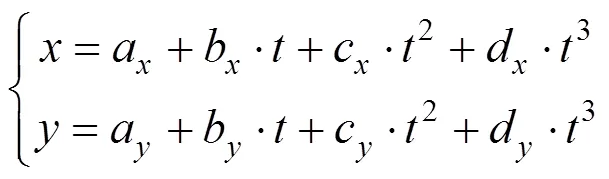
根据式(1)，设该曲线的矢量表达式为

其一阶求导式为

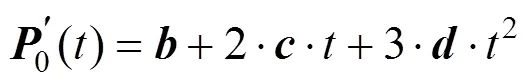
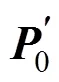
最后将式(4)中的各系数值带入式(2)中即可得三次Hermite插值参数函数一般式

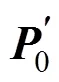
本算法中即采用三次Hermite插值参数函数即式(5)计算采样点间的插值点进而逼近隐式曲线。

2 算法梗概

本文平面隐式曲线Hermite插值逼近算法的处理过程分为3步：网格化获取采样点、优化采样点和曲线折线化。

(1) 网格化获取采样点。首先将曲线绘制区域网格化，再在网格单元各边中通过线性插值计算曲线采样点。

(2) 优化采样点。为减少数据量，提高绘制质量和逼近精度，本算法对采样点进行了优化处理，优化前判断采样点能否被精简，即计算采样点精简前后构成的曲线之间产生的误差是否符合优化要求，若符合优化要求则其可被精简。

(3) 曲线折线化。对于优化后的采样点通过Hermite插值逼近隐函数曲线。

3 算法步骤

3.1 网格化获取采样点

本算法借鉴MC方法，通过网格离散化后获取曲线采样点。MC算法是一种经典的基于体元构造等值面的算法，其主要思想是将三维构造空间划分为一定数量的体元，再将体元的每个顶点进行分类标记，然后对顶点标记互异的边通过插值法求出采样点，最后用三角面片逼近等值面。该方法也可降维应用于二维等值线的绘制(称其为二维MC算法)，具体内容为将绘制区域网格离散化，并对每个网格单元顶点分类标记，然后对顶点标记互异的边通过插值法求出采样点，最后在对采样点不做任何处理的情况下将其连接起来，从而绘制出曲线。虽然MC算法中采样点连接存在复杂的二义性问题，但是该算法原理简单、容易实现，因此得到了广泛的应用。

获取采样点的思路为：设隐函数(,)=0，在平面上均匀地构造×个网格单元，并获取每个网格单元顶点的坐标及函数值，若函数值大于或等于0的顶点标记为“+”，小于0则标记为“–”。假设采样点在网格单元内是线性变化，那么可推断，网格中存在两端点标记分别为“+”和“–”的边上存在采样点，便可通过线性插值确定该点。但是算法中可能出现二义性，图1中的网格单元边存在采样点、、、，其连接顺序即会出现图1中(a)和(b)两种情况。为解决此问题，本算法首先计算出每个网格单元中心点坐标、函数值和标记，进而在每个网格单元中构造4个三角形如图2(a)所示，以Δ012为例，采样点的情况将会有图2(b)~(e) 4种情况(图中的点1、2为获取的采样点)，如此便可避开图1中可能出现的二义性。

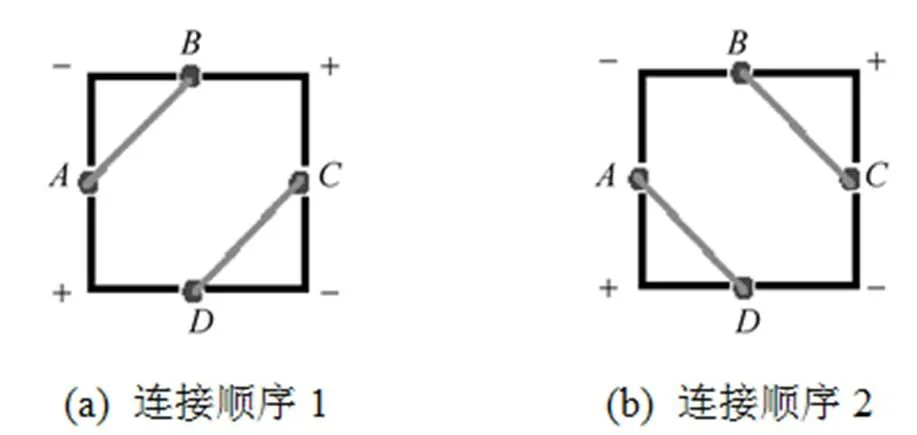
图1 二义性情况

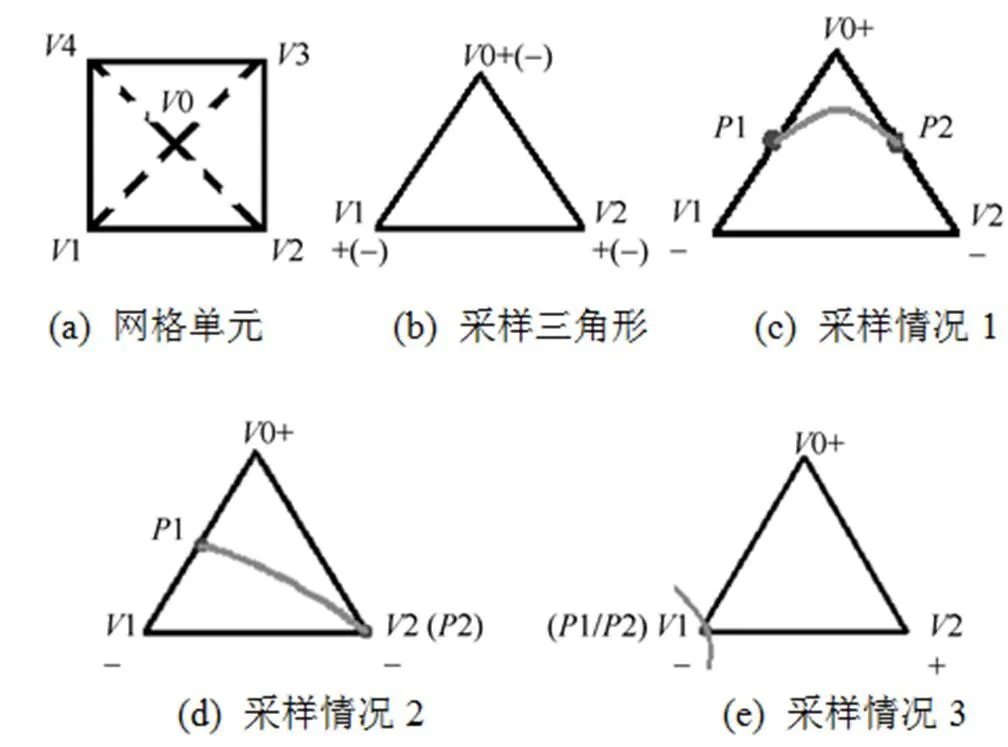
图2 网格单元及采样情况

3.2 优化采样点

为减少数据量，本算法对采样点进行了优化。判断采样点能否被精简的要求是：采样点精简前后构成的曲线之间产生的误差大小。如图3所示，设待精简采样点、、、、5点连接而成的原始折线段Line，由Hermit插值法计算出、之间的插值点、、、构成的折线段来逼近Line。不难发现采样点精简前后产生的误差可由图中阴影部分的面积表示。假设允许误差不能超过，若≤，满足优化要求，即可精简、、3点，反之则不能精简。那么计算出阴影面积即成为采样点优化的关键。本算法通过求两条折线段的交点和计算多边形面积两步完成阴影面积的计算。

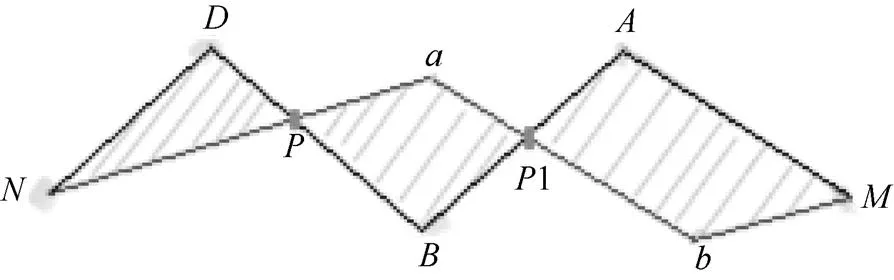
图3 误差示例图

交点计算方法以图3中与两折线段为例，设其交点为。设线段、的矢量方程分别为

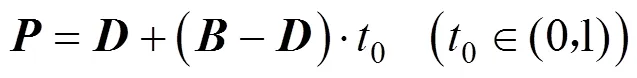
其中，0、1为定比参数。假设两折线段有交点，联立式(6)、(7)可得

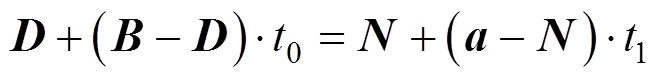
计算可得0、1的解。若0、1有无穷解，则两线段关系为平行或重合；若0、1有唯一解，且0、1的值均在(0, 1)，即可判定两线段有且只有一个交点，将其代入式(6)或式(7)可求出交点。

误差面积计算方法以图3中多边形面积为例。其计算方法为在平面内任取一点，如图4所示，通过三角形向量面积公式计算出Δ、Δ、Δ的面积，其和的绝对值为Δ面积，即S=|S+S+S|。依次类推，计算出图3中所有多边形面积之和为=|S+S1+S1|，即为折线段Line精简前后的误差。判断与的大小关系，即可判断采样点能否优化。

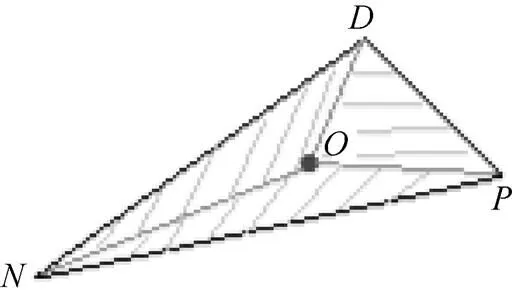
图4 多边形NDP

3.3 曲线折线化

对于精简后的采样点集，分别计算出各点切向，通过三次Hermite参数函数式(5)按点序分段插值逼近隐式曲线，其中插值点数量根据实际曲线光滑度要求进行设置。

4 实验与数据

利用本算法在PC机上基于Windows平台和OpenGL图形设备接口及Visual C++6.0实现了如下隐式函数曲线的绘制

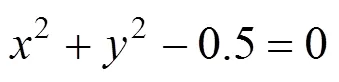
为方便说明和比较，本文中的曲线均在30×30的网格中获取采样点绘制曲线，表1为各曲线在不同允许误差的情况下采样点优化情况，从表1可知，允许误差越大，优化率越大，优化后采样点个数越少；反之允许误差越小，其优化率越小，优化后采样点个数越多。同时结合曲线绘制结果可知同一隐函数曲线随着允许误差逐渐增大，曲线光滑度也随之变化，其中≤10-6和≤10-5情况下，曲线光滑度较为乐观，而在≤10-3情况下，曲线光滑度较低(图5)。表1中，可简单得出结论曲线优化率与其形状复杂度存在关系；从图6中可看到，四角星中存在切向矢量值变化较大的4个角的采样点，即使经过优化处理之后，本算法也能保留切向矢量值变化较大的点，从而确保了曲线特征的完整性。

因本算法借鉴了MC算法思路获取采样点，并与二维MC算法绘制的隐式曲线情况作了对比，显示有一定的可比性，能说明本算法中采样点优化情况。通过实验可发现，在同等网格数量30×30条件下，二维MC算法绘制的隐式曲线光滑度和准确度与本算法允许误差≤10-6的情况相似，对比这两种情况下绘制隐式曲线的采样点数量更有说服力。从图7中可看出，本算法若要达到与MC算法同等的光滑度，对于较简单的曲线(如圆、圆角矩形等)本算法可通过约其采样点数量的1/4即可实现，对于特征较多的曲线(如心形曲线、四角星曲线、花形曲线等)，本算法可通过约其采样点数量的1/2即可实现。

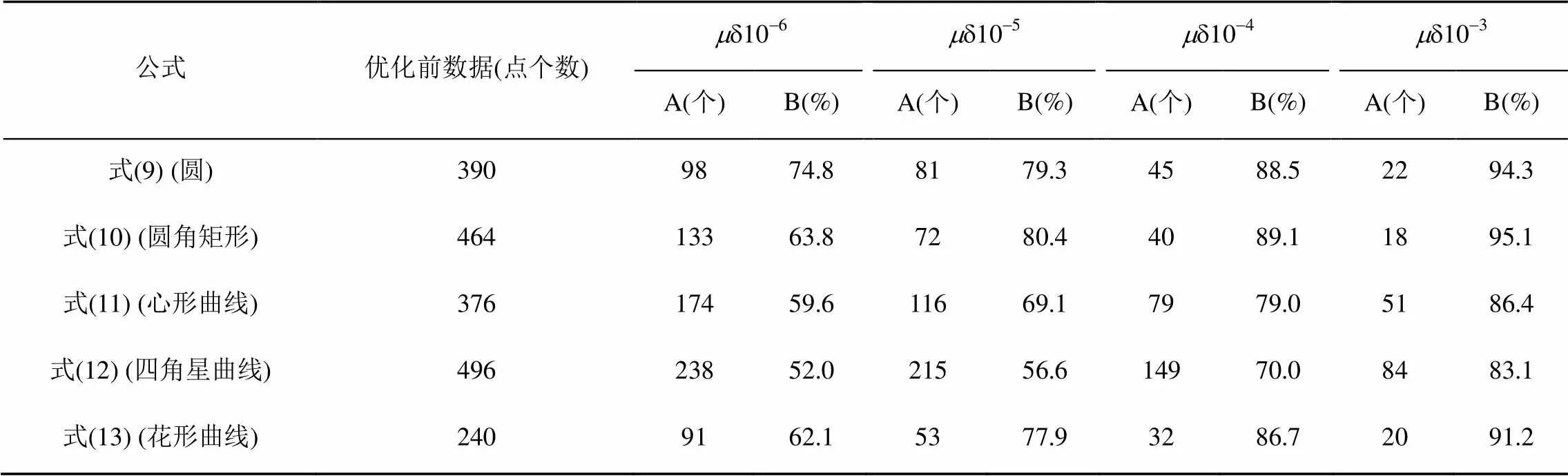
表1 不同允许误差m情况下采样点个数及压缩率比较

注：A表示优化后数据点个数，B表示优化率

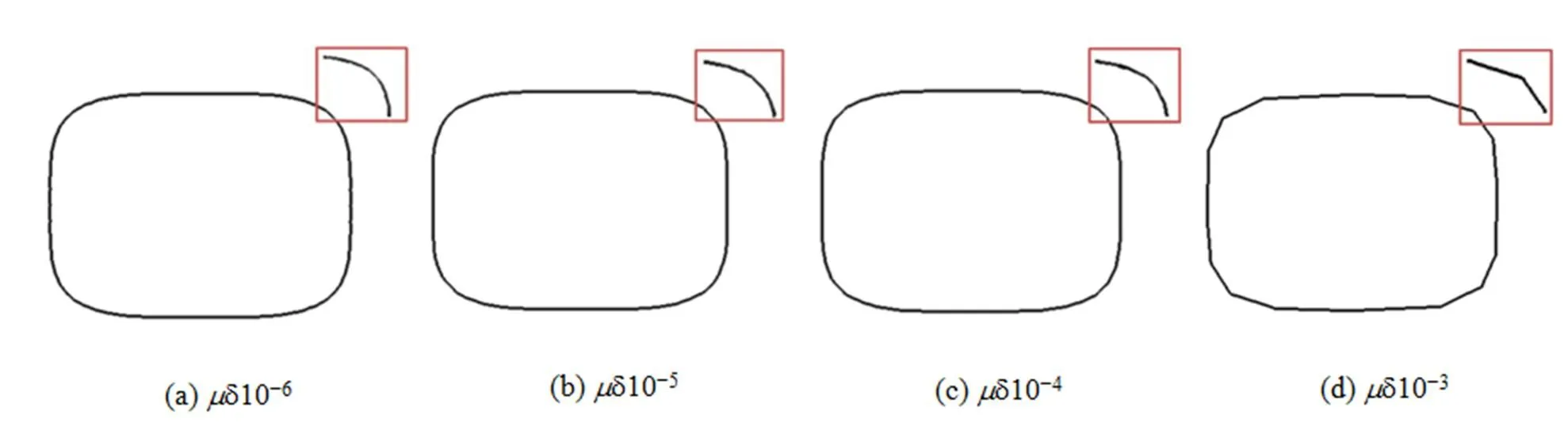
图5 圆角矩形(式(10))曲线在不同允许误差下的绘制情况

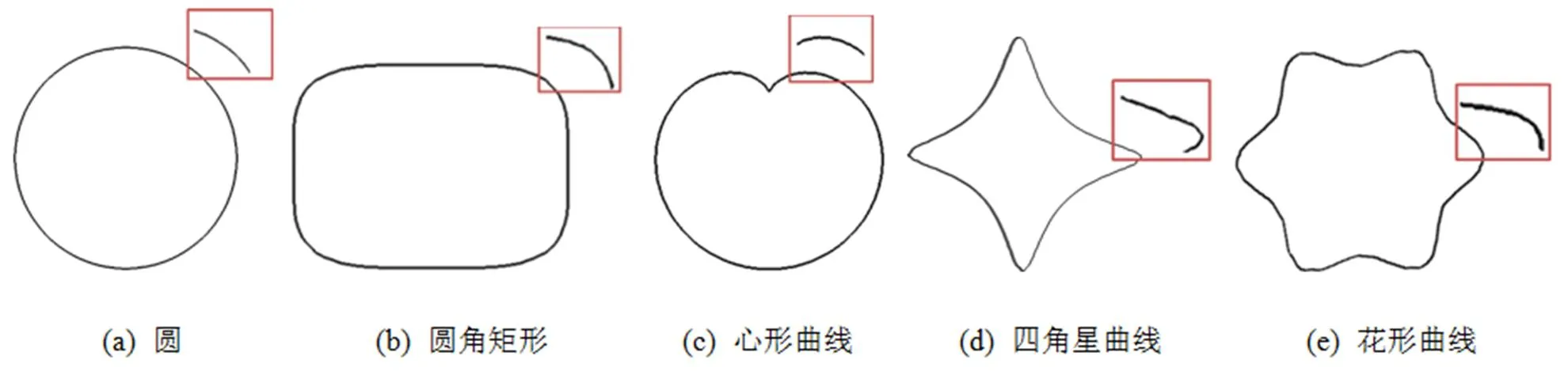
图6 允许误差为m≤10-5情况下各隐式曲线绘制情况

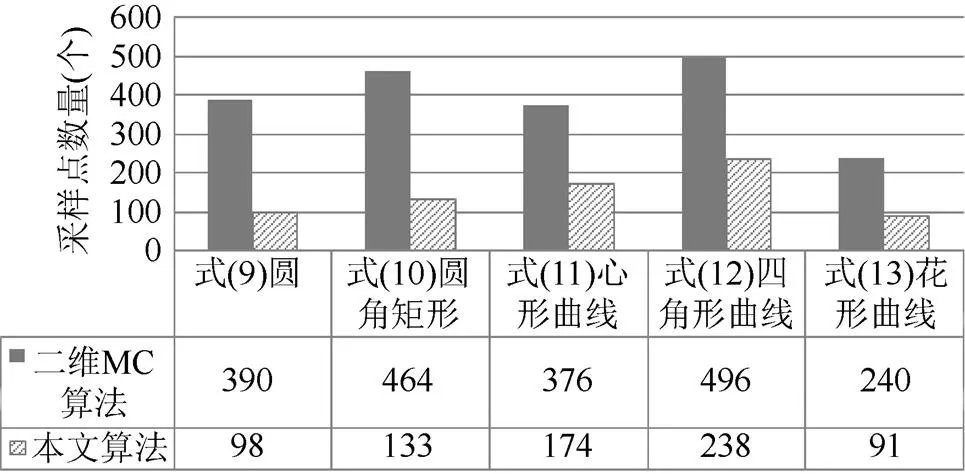
图7 二维MC算法与本文算法允许误差为m≤10-6情况下采样点数量对比图

5 结束语

本文给出的平面隐式曲线的Hermite插值逼近算法，成功地实现了隐式曲线的绘制。从实验结果可看出，采样点优化率可观，有效地节省了存储空间，还可根据不同误差要求控制采样点优化数量和曲线光滑度。虽然此算法能较好地处理切向矢量值变化较大的采样点，但是其绘制类似四角星4个角尖点时光滑度不理想，这将在后续工作中有待进一步探讨与改进。

[1] 徐国良. CAGD中的隐式曲线与曲面[J]. 数值计算与计算机应用, 1997, 18(2): 114-124.

[2] 刘颖. 复杂的隐式函数曲线绘制算法的研究[D]. 长春: 长春大学, 2006.

[3] 张三元, 孙守迁, 蒋方炎, 等. 数字化仿真人体模型的设计方法[J]. 系统仿真学报, 2000, 12(1): 49-50.

[4] 温维亮, 郭新宇, 陆声链, 等. 隐式曲面在三维植物建模中的应用研究综述[J]. 图学学报, 2010, 31(3): 1-10.

[5] 赵伟, 赵卓宁, 李五生. 一种有效的离散数据场等值线生成方法[J]. 成都信息工程学院学报, 2007, 22(1): 116-121.

[6] SHELBERG M C, MOELLERING H, LAM N. Measuring the fractal dimensions of empirical cartographic curves [C]//Auto-Carto 5. Virginia: American Academy of Photometry and American Congress on Surveying and Mapping, 1982: 481-490.

[7] SUNDARAMOORTHI G, YEZZI A, MENNUCCI A. Coarse-to-fine segmentation and tracking using Sobolev active contours [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(5): 851-864.

[8] TAUBIN G. Distance approximations for rasterizing implicit curves [J]. ACM Transactions on Graphics, 1994, 13(1): 3-42.

[9] 童若锋, 汪国昭, 金通光. 轮廓跟踪的TN方法[C]//第一届全国几何设计与计算学术会议论文集. 东营: 中国石油大学出版社, 2002: 579-582.

[10] 余正生. 隐式曲面造型与绘制算法研究[D]. 杭州: 浙江大学, 1999.

[11] 蔡耀志. 正负法数控绘图[J]. 工程图学学报, 1984, 5(Z1): 3-9.

[12] 吴坚, 张接信, 蔡宗琰. 用短线截交法绘制隐式曲线[J]. 机械科学与技术, 2006, 25(8): 965-966.

[13] SUFFERN K G. Quadtree algorithms for contouring functions of two variables [J]. Computer Journal, 1990, 33(5): 402-407.

[14] DUFF T. Interval arithmetic recursive subdivision for implicit functions and constructive solid geometry [J]. ACM Computer Graphics, 1992, 26(2): 131-138.

[15] 寿华好, 何苹, 缪永伟. 自动微分在隐式曲线绘制中的应用[J]. 计算机工程与应用, 2009, 46(1): 150-153.

[16] LORENSEN W E, CLINE H E. Marching cubes: a high resolution 3D surface construction algorithm [J]. ACM Computer Graphics, 1987, 21(4): 163-169.

[17] 李洪发. 分段三次Hermite插值的同时逼近[J]. 天津师范大学学报: 自然版, 2012, 32(2): 38-40.

[18] FUHRMANN S, KAZHDAN M, GOESELE M. Accurate isosurface interpolation with hermite data [C]// 2015 International Conference on 3D Vision. New York: IEEE Press, 2015: 256-263.

Approximating Planar Implicit Curves with Hermite Interpolation

WEI Li, ZHAO Jingjie, HUANG Huimin

(Institute of Educational Information Engineering, Nanjing Normal University, Nanjing Jiangsu 210097, China)

Implicit curves play an important role in medical image processing, geographic information system, and numerical field visualization. On the basis of sampling point analysis and curve approximation method, we introduce an algorithm for approximating planar implicit curves by means of Hermite interpolation. The sampling points were firstly obtained by linearly interpolating each edge of the grid cells distributed uniformly in the grid region. Then, we calculated the error between curve segments before and after optimizing. Once the error meets the optimizing requirements, the sampling points are consequently optimized. Finally, the algorithm approximated the implicit curves by the Hermite interpolation method. Experiments have shown that even when the number of sampling points is small, the curves drawn by the algorithm still have relatively higher smoothness and accuracy.

graph plotting; implicit curve; Hermite interpolation; optimizing sampling point

TP 391.41

10.11996/JG.j.2095-302X.2018040752

A

2095-302X(2018)04-0752-05

2017-10-20；

2017-12-19

全国教育科学“十三五”规划2017年教育部重点课题(DCA170302)

魏 利(1994-)，女，四川绵阳人，硕士研究生。主要研究方向为数字几何处理。E-mail：wei_li_015@163.com