提高神经网络泛化能力的方法研究及仿真

南昌航空大学信息工程学院 罗艳芬

神经网络泛化能力是衡量神经网络性能优劣的一个重要方面，研究了几种提高神经网络泛化能力的方法，并且利用MATLAB仿真验证了各种方法的有效性。

引言

泛化能力是指经训练（学习）后的预测模型对未在训练集中出现的样本做出正确反映的能力，学习不是简单地记忆已经学过的输入，而是通过对有限个训练样本的学习，学到隐含在样本中的有关环境本身的内在规律性。尽管神经网络可以具备泛化能力，但大量的设计者在应用神经网络时都发现，获得好的泛化能力并非易事，它涉及的方面非常复杂。因此对于如何提高神经网络泛化能力，研究者们展开了大量的研究。

1.贝叶斯统计及其正则化

用于训练多层感知器的传统方法在统计学上可以解释为一种最大似然估计的变形实现，其思想是找到一组权值来尽可能地拟合训练数据。

图1 -1 无贝叶斯正则化训练结果

图1 -2 贝叶斯正则化训练结果

在贝叶斯正则化模式中，假设神经网络的权值和偏置满足特定的概率分布，用概率规则来实现学习和推理，对这些参数进行估计。贝叶斯定理的计算学习机制是将先验分布中的期望值与样本均值按各自的精度进行加权平均，精度越高者其权值越大。由于贝叶斯方法可以综合先验信息和后验信息，既可避免只使用先验信息可能带来的主观偏见和缺乏样本信息时的大量盲目搜索与计算，又可避免只使用后验信息带来的噪声影响。

以一个带噪声的正弦信号拟合仿真为例，在网络训练过程中不用贝叶斯正则化方法和应用贝叶斯正则化方法得到的拟合效果如图1-1、 图1-2所示。图中虚线为实际的带噪正弦信号，实线为神经网络拟合信号。显然，应用贝叶斯正则化方法得到的拟合效果更好。

2.权值衰减

权值衰减是在网络训练误差函数中加入对权值惩罚项。作用就是惩罚大的权值，使权值收敛到绝对值较小的范围中去。另外，当训练集容量较小时，神经网络模型的泛化能力受衰减常数的影响较大。通常情况下，均方误差函数表达式为：

权值衰减是在误差函数中加入对权值惩罚项，即：

以普通均方误差函数训练神经网络得到的仿真结果为例，仿真结果如图2-1所示：

图2 -1 普通均方误差函数训练结果

若在均方误差函数中加入权值衰减项，训练神经网络得到的仿真结果如图2-2所示。

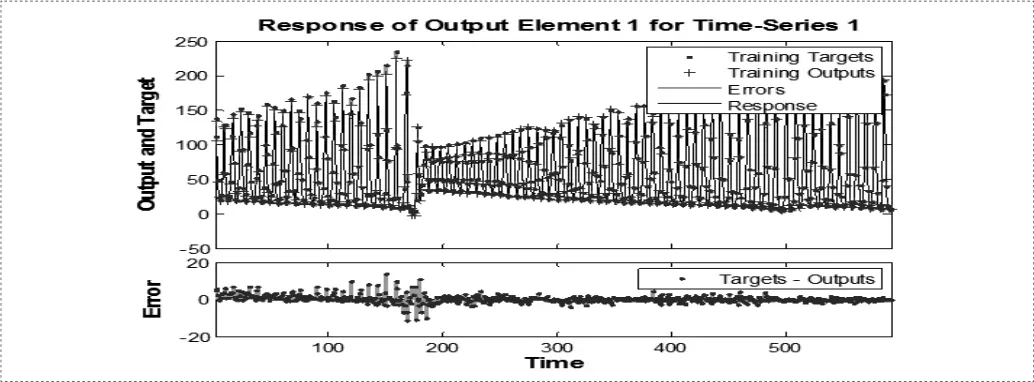
图2 -2 权值衰减的均方误差函数训练结果

由仿真结果可以看出，经过权值衰减，网络训练误差大大降低，网络输出和目标值逼近效果更好。

3.神经网络集成

神经网络集成是指对同一问题用多个神经网络进行学习，集成在某一输入下的输出由构成集合的各个网络的输出共同决定。神经网络集成提出的主要目的是为了解决单个网络存在的问题。为了解决由于噪声数据或训练集很小引起的泛化问题，提高神经网络的泛化能力，一种有效的方法是训练多个神经网络并且对它们的输出取均值。

例如，训练10个神经网络，得到10个训练均方误差值，对10个神经网络的输出取平均值，并利用输出平均值计算网络训练均方误差，并分别进行比较。具体实现过程如下：

每个神经网络的训练均方误差如下所示：

对各个神经网络输出取平均值，并以此作为神经网络输出计算均方误差平均值。

运行结果为：

很显然，用输出平均值计算的均方误差比每个神经网络的均方误差值都小，如果增加训练数据，仿真结果会更好。

4.结论

本文针对贝叶斯统计正则化方法，权值衰减方法以及神经网络集成方法进行研究，并利用MATLAB仿真验证各种方法提高神经网络泛化能力的效果。仿真结果表明，通过应用这些方法，神经网络训练误差大大降低，泛化能力大大提高。