基于多元线性回归的月度牛奶产量预测

王尔东

0 引言

随着社会经济的发展和人民生活水平的提高，牛奶及其相关产品已经成为人们日常生活重要的一环。从一个角度来说，社会需求量的上升导致了奶价上升，缺乏科学客观的牛奶产量预测会对人民生活产生影响；从另一个角度来说，牛奶产量是奶业的基石，对牛奶产量的科学预测对生产者具有十分重要的现实意义。通过对牛奶产量的预测，不仅可以探索其发展变化的规律，而且能为奶业的生产制造者提供有意义的指导，从而进行合理的牛奶生产，避免浪费，提高经济效益的同时进一步为社会提供正确的消费导向，促进奶业与消费者之间的良性循环。

关于月度牛奶产量这样的时间序列数据，在文献调研中并没有发现相关研究。但是，对于年度、季度牛奶产量的数据却有所涉及。文献[1]应用灰色模型(gray model,GM)GM(1,1)对新疆牛奶产量发展进行预测，结果表明该模型有较高的可靠性和实用性，能够对新疆的奶业发展能够起到一定的导向作用。文献[2]应用ARIMA(Autoregressive Integrated Moving Average Model,ARIMA)模型对河北省的牛奶产量进行预测，结果表明该模型具有良好的预测效果和应用价值，可以对河北省牛奶产品进行合理并准确的分析。文献[3]应用多元线性回归模型(multivariable linear regression model,MR)对短时交通流量进行预测，结果表明该模型预测精度良好。文献[4]应用贝叶斯网络对牛奶产量进行预测，结果表明该模型在理论上具有严格性与统一性，能有效直观地进行预测。文献[5]应用MR对成品油价格进行了预测，结果表明多元线性回归模型达到了较好的效果。

1 多元线性回归

多元线性回归在与预测相关的研究中有广泛的应用。多元线性回归模型根据历史的样本数据,建立多元线性回归的预测模型，从而预测未来时刻多元线性回归模型中的回归参数。通过一些的模型精度评估指标.对多元线性回归模型参数的预测进行评测,选择最优的预测模型，从而表明这个模型可以用于分析和预测因变量对自变量的回归关系问题。

多元线性回归利用以下的原理进行计算：假设自变量与因变量之间存在着线性关系，用一定的线性回归模型来拟合自变量与因变量之间的关系，并通过确定模型参数来得到回归方程。然后，可以通过此回归方程来分析变量之间的相关关系，进而能够检验、分析各个自变量对因变量的线性影响。多元线性回归模型在时间序列预测中的应用可以表示为公式(1)，这里Yt是因变量的预测值，是通常应用最小二乘法确定的回归系数，是回归方程的常数项，是自变量，e代表误差。

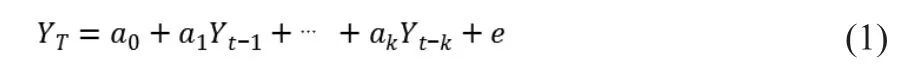
公式(1)表明它表明被解释变量Yt的变化由两部分进行解释。第一，由t个解释变量Y的变化引起的Yt的线性变化部分；第二，由其他随机因素引起的Y的变化部分，e为随机误差；a0是回归方程的常数项；是回归系数；t=1，2，…，n，以上随机因素引起的变化。

2 研究方法

本文的整体研究框架大致分为以下几个步骤：首先进入https://datamarket.com/data网站搜集某地1962年1月至1975年12月的牛奶产量数据并整理成“.csv”格式的数据文件，再将数据进行预处理（时间序列化）。接下来将数据文件导入R语言环境，并进行模型参数设置，将数据分为训练集和测试集后，使用rminer程序包中的MR模型进行预测，计算预测精度，最后调整参数，选择最高预测精度的模型，验证模型的准确性。

整个预测过程的实现程序如算法1所示。首先导入“rmin-er”的程序包，然后将月度牛奶产量数据通过“read.csv("数据文件路径名称",header=TRUE)”函数读取进来，并保存到“tab”这个变量中；之后将tab中的“每月产量”这一列数据通过代码da=tab$production将其提取出来，并对其进行时间序列化。然后设置模型参数，通过代码“window=12”调整窗口长度为12，通过代码“H=12”调整测试集大小为12；接着通过代码“L=length（a）”计算数据长度；最后再设置测试集；下一步通过代码“d=CasesSeries(a,c(1:window)”将所有数据转化为矩阵d，再通过代码“LD=nrow(d)”计算其行数，最后通过代码“dtr=1:(LD-H)”设置训练集的行数，参数调整完成。接着使用fit()函数建立多元线性回归模型，同时运用lforecast函数建立预测模型并保存至变量pred中，再建立变量r表示预测值与测试集在RMSE运算后的误差并做出图像，最后显示出预测值与测试集分别在RMSE和MAE度量标准下的误差值。

本实验的步骤与代码设计如表1所示：

表1 实验步骤与代码设计

3 实验

3.1 实验准备

本实验采用的是美国某地1962年1月至1975年12月的月度牛奶产量，共158个数据点，由Time Serious Data Library提供。本实验的数据整体呈波动上升趋势。

本实验的程序编写语言与操作环境是R，R用于统计分析、绘图的语言和操作环境，是一个自由、免费、源代码开放的软件。本实验使用了rminer程序包，提供用户可视化的角色挖掘和角色状态更新平台。

本实验运用了RMSE与MAE两种度量标准，

其中yt为预测值，ft为真实值，T为测试点个数。

3.2 实验验证

本实验根据参数中的窗口长度window作为变量，通过等距调整window的值记录，因变量预测精度，得到的实验设计结果。由实验得出的图表可以得出以下结论与分析：

（1）总体来说，多元回归模型对于月度牛奶产量的预测是十分优秀的，能够成功得出对未来牛奶产量的科学预测。

（2）预测精度在参数window的变化下逐渐趋于稳定。预测的误差在window值取2至10是快速下降，并且预测精度急剧升高，预测性能越来越好。

（3）在window值取8时，预测精度最高；随着window值的升高，图像始终在实际数据上下波动，且波动幅度较小。

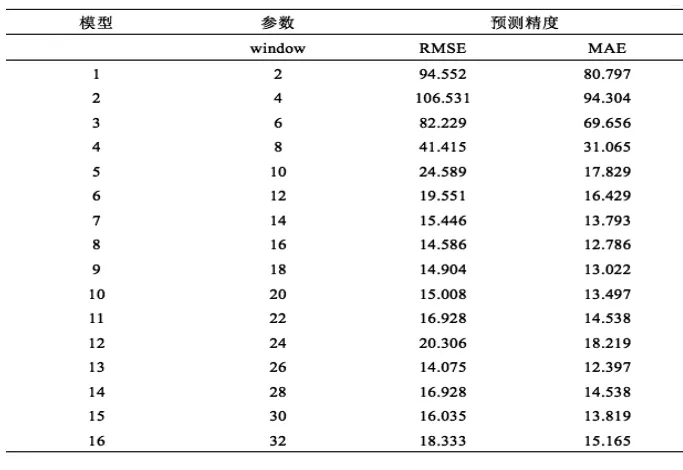
表2 MR模型对该地1975年1月至12月月度牛奶产量预测的实验结果

4 结论

本文运用多元线性回归模型，从1962年1月至1974年12月月度牛奶产量的数据出发，通过数据时间序列化和建模预测，成功对1975年1月至12月月度牛奶产量进行了科学的预测。并且通过均方根误差（RMSE）与平均绝对值误差（MAE），计算了不同窗口长度下多元线性回归模型的预测精度。其中，窗口长度为8的模型误差值更小，预测精度更高。