基于Pan-Tompkins的运动心电QRS波群实时检测的研究
苏志同,吴琼琼
基于Pan-Tompkins的运动心电QRS波群实时检测的研究
苏志同,吴琼琼
(北方工业大学 计算机学院,北京 100144)
对处于运动状态的人进行实时心电检测,及时了解心脏状况,可以很大程度上减少人们由于心脏疾病引发的死亡。QRS波群的实时检测是运动心电分析过程中的重要研究内容,检测正确的QRS波群或R峰值是心电图测量的重要指标。本文利用Pan-Tompkins算法对运动心电数据进行QRS波群的实时检测,结果表明,该方法适合实际应用。
运动心电;QRS波群;Pan-Tompkins算法
0 引言
目前,心脑血管疾病仍旧是危害人类生命健康的主要疾病之一[1]。尤其是在运动过程中,人们必须经常性的关注自己的心电状况,适当的调整运动量,避免运动过量造成身体的不适甚至猝死等特别严重的后果。心电图是临床上检测心脏疾病的重要手段,由于心电图检查简单、准确、快速、无创,所以心电图(ECG)对于心脏疾病的诊断有着非常重要的意义。对于心电图的分析一般都是事后进行分析,不能达到实时诊断的要求,也达不到预警的目的。在移动医疗科技水平迅速发展的条件下,对人的运动心电状况进行实时检测,分析心电变化趋势,能够对未来用户身体状况进行预测。
心电图(ECG)信号是通过测量来自心脏肌肉活动而产生的电信号。它是一种非侵入性的仪器,由于心电图的这一特性,它被广泛用于心血管疾病的诊断。它也是生物医学信号处理领域最受欢迎的研究领域之一,其应用范围从自动检测心律失 常[2-4],睡眠呼吸暂停[5,6]到心理应激[7,8]。在自动心电信号处理中,研究的主要课题之一是QRS波群检测。检测正确的QRS波群或R峰值很重要,因为它是用来测量其他ECG指标的,如RR间隔,QRS宽度和心率变异性(HRV)。这些度量标准通常用作ECG分类的特征。
1 QRS波形检测
QRS波群检测和特征提取是心电图自动分析的关键步骤,直接影响心脏疾病检测和诊断的准确性以及可靠性。由于QRS波群振幅大,占的时间比较短,只有QRS波群的位置确立以后才可以分析心电图的其他波形,所以QRS波群位置的确定成了ECG检测的重要环节。
目前,QRS波形检测方法都是针对静态或动态心电进行检测,方法很多,如小波变换、神经网络、模板匹配等方法。小波变换具有时域和频域特性,算法检测的准确度相对很高,但是小波变换的计算复杂度很大,不适合处理实时的心电数据。虽然神经网络能够很好的识别QRS波群,但是由于神经网络的训练时间比较长,难以在现实生活中得以实际应用。模板匹配法虽然原理简单,但容易受到高频噪声和基线漂移的干扰。以上的几种方法都有各自的优点和缺点,相比较Pan-Tompkins算法检测效果和实时性比较好,在实际应用中可以被采用。
Pan-Tompkins是Pan和Willis J. Jiapu Tompkins提出的一种算法[9],可以用来实时检测心电图的QRS波群。该算法在检测QRS波群方面具有良好的性能,并且可以应用于移动应用。所以,针对在实时远程运动心电监护系统中QRS波的实时检测分析问题,本文利用Pan-Tompkins算法对运动心电数据进行QRS波群的实时检测。具体步骤如图1所示。

图1 QRS波群检测步骤
1.1 数据预处理
心电信号非常微弱,容易受到环境的影响。心电在采集的过程当中会受到各种各样的噪声干扰,尤其是运动心电信号,运动时的呼吸、肌肉的抖动、甚至出汗都会增加很多噪声的干扰。运动心电的噪声主要有三种类型:工频干扰、肌电干扰、基线漂移。在QRS波群的检测中,心电去噪是十分重要的。结合去噪的效果和实时性,采用级联低通和高通滤波器组成的带通滤波器去除原始运动心电信号中的噪声。
低通滤波器:低通滤波器用于降低工频干扰和T波干扰,该滤波器的差分方程为:

截止频率约为11Hz,增益为36。
高通滤波器:高通滤波器的设计基于从全通滤波器(即,原始信号中的采样)中减去一阶低通滤波器的输出。这种高通滤波器用于减少肌电干扰和基线漂移。该滤波器的差分方程为:

该滤波器的低截止频率约为5 Hz,即增益是32。
1.2 获取QRS波群的斜率信息
在滤波之后,采用具有传递函数的五点微分函数,放大QRS波的斜率信息,以便区分QRS波群。五点微分函数的差分方程为:

1.3 增强频率响应曲线的斜率
微分后,信号逐点平方,这个操作公式为:
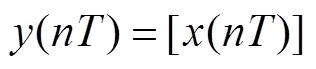
该步骤使用非线性平方函数,使得所有数据点都为正。对微分后的输出进行非线性放大,以增强微分后频率响应曲线的斜率,并且有助于限制由高于平常光谱能量的T波引起的误差。
1.4 获得波形特征信息
信号逐点平方后,进行移动窗口积分。目的是除了获得R波的斜率外,还可以获得波形的其他特征信息。移动窗口积分器产生一个信号,其中包含QRS波群的斜率和宽度的信息。计算公式如下:

其中是积分窗口宽度中的样本数,窗口的宽度应尽可能和QRS波群宽度大致相同。如果窗口太宽,积分波形会将QRS波群和T波合并在一起。如果它太窄,一些QRS波群将在积分波形中产生多个峰值。这将对QRS波群的检测过程造成困难。
1.5 自适应阈值,检测QRS波群的位置
QRS波群对应积分波形的上升沿。上升沿的持续时间等于QRS波群的宽度。QRS波群的时间位置的基准标记可以根据待标记的期望波形特征(例如R波的最大斜率或峰值)从该上升边缘确定。阈值会自动调整以漂浮在噪声上。由于带通滤波器改善了信噪比,所以可能出现低阈值。我们使用两组阈值来检测QRS波群,两个阈值中的较高值用于信号的第一次分析。如果在特定的时间间隔内未检测到QRS,则使用较低的阈值。对于QRS波群检测来说,搜索回溯技术是必要的。
最初应用于积分波形的一组阈值是从下面公式计算出来的:
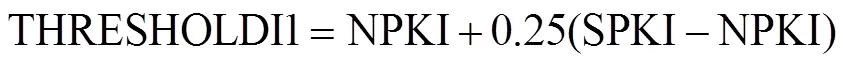
NPKI是噪声峰值
SPKI是信号峰值
THRESHOLD I1是较高阈值
THRESHOLD I2是较低阈值
2 实验结果
在这次实验中,我们使用两种类型的心电数据。第一种是MIT-BIT的心率失常数据库,第二种是麦邦运动心电监测设备所采集的心电数据。第一种数据是用来进行测试以及验证该算法的正确性,第二种数据是用来观察该算法的实用性。
对MIT-BIT数据库中的一些病例进行了QRS波群的检测,该方法的检测效果很好,整体准确率达到92.5%,其中对于107、205、217号数据,漏检的数量比较多,原因是因为这几组数据中夹杂了严重的伪差,导致QRS波形严重失真,于是造成了漏检的情况。检测的结果如表1所示。
表1 MIT-BIT数据库QRS波群检测结果

Tab.1 Detection results of QRS complexes in MIT_BIH database
此外,根据该算法对麦邦运动心电监测设备所采集的心电数据进行测试,同样取得了很好的检测效果,证明该算法对运动心电QRS波群的检测具有可靠性以及有效性。
根据Pan-Tompkins算法,经过级联低通高通滤波器、微分、平方、移动窗口积分处理后,得到与QRS波群一致的波形特征,如图2所示。算法在MATLAB上实现的,同一窗口(figure)显示六块图形,分为三行两列。从左到右,由上至下依次为:原始信号、低通滤波后信号、高通滤波后信号、微分后信号、平方后信号、移动窗口积分后信号。
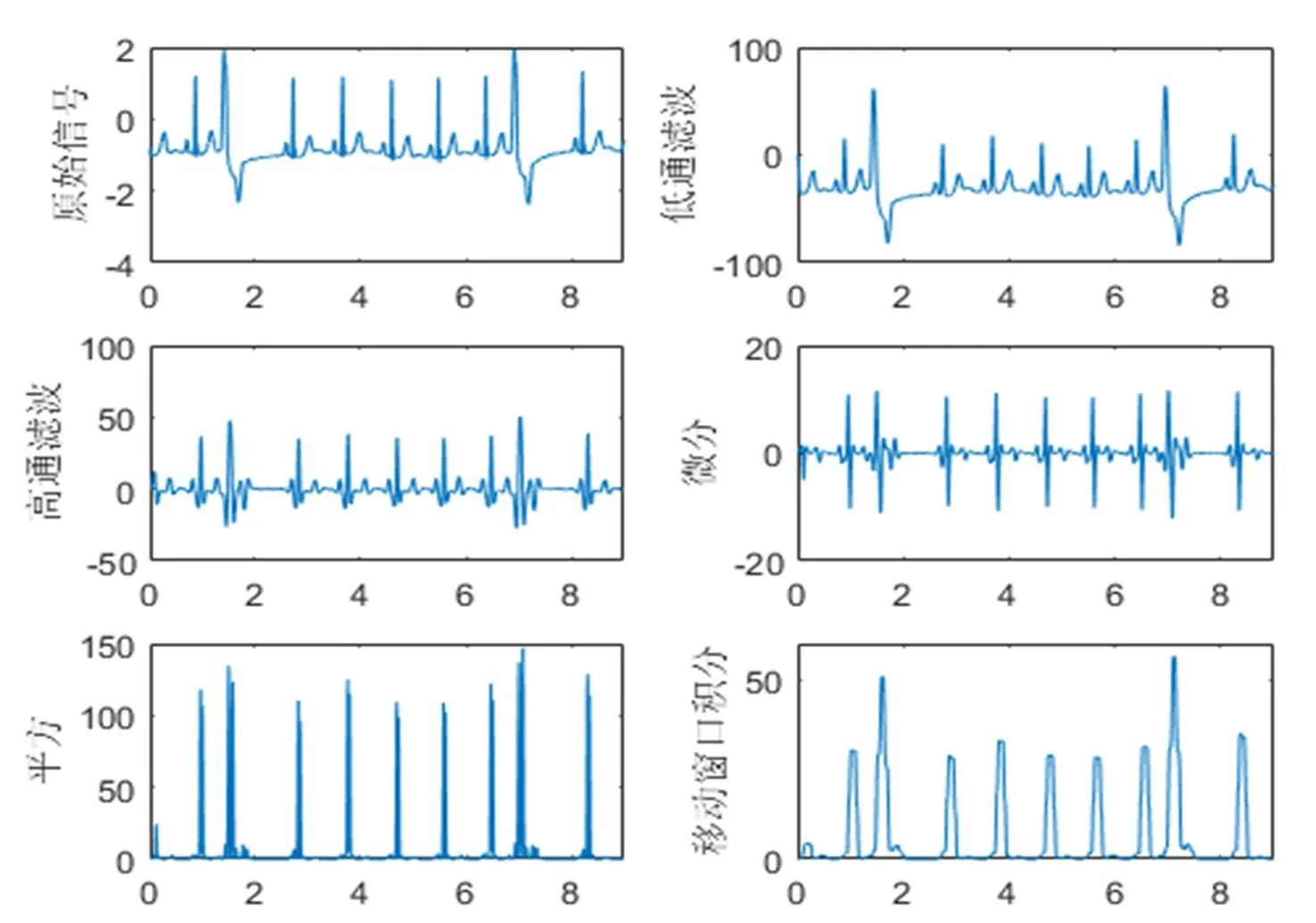
图2 处理后波形
自适应阈值调节后,能够准确地区分QRS波群的位置。QRS波群特征点检测结果如图3所示。在图3中,紫色标记的为Q点的位置,R峰由红色进行标记,绿色标记的为S点的位置。
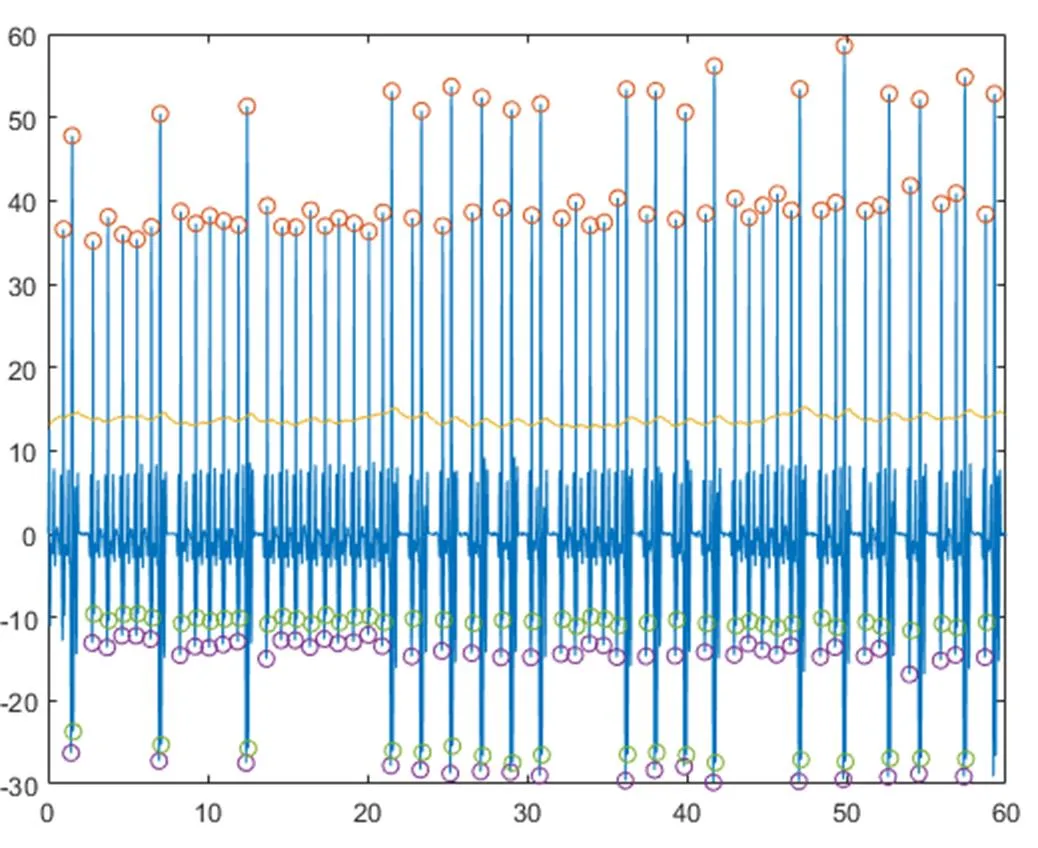
图3 QRS波群检测结果
3 结论
本文提出使用Pan-Tompkins算法对运动心电QRS波群进行实时检测。该算法利用斜率、振幅和宽度信息可靠地检测QRS波群。带通滤波器对信号进行预处理以减少干扰,允许使用低振幅阈值以获得高检测灵敏度。在算法中,采用双阈值技术和搜索回溯技术进行漏检,该算法周期性地自动适应每个阈值和RR区间限制。实验说明,Pan-Tompkins算法可以在运动心电QRS波群检测中运用,并且计算量很小,适合于实时应用。
[1] 郭文灵, 顾建军. 移动心电监护系统的心电图实时分析算法[J]. 计算机仿真, 2014 (2014年09): 272-276.
[2] De Chazal P, O'Dwyer M, Reilly R B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features[J]. IEEE transactions on biomedical engineering, 2004, 51(7): 1196-1206.
[3] Luz E J S, Schwartz W R, Cámara-Chávez G, et al. ECG-based heartbeat classification for arrhythmia detection: A survey[J]. Computer methods and programs in biomedicine, 2016, 127: 144-164.
[4] Escalona-Morán M A, Soriano M C, Fischer I, et al. Electrocardiogram classification using reservoir computing with logistic regression[J]. IEEE journal of biomedical and health informatics, 2015, 19(3): 892-898.
[5] Hassan A R, Haque M A. Computer-aided obstructive sleep apnea screening from single-lead electrocardiogram using statistical and spectral features and bootstrap aggregating[J]. Biocybernetics and Biomedical Engineering, 2016, 36(1): 256-266.
[6] Hassan A R, Haque M A. An expert system for automated identification of obstructive sleep apnea from single-lead ECG using random under sampling boosting[J]. Neurocomputing, 2017, 235: 122-130.
[7] Lampert R. ECG signatures of psychological stress[J]. Journal of electrocardiology, 2015, 48(6): 1000-1005.
[8] Han, Lu, et al. "Detecting work-related stress with a wearable device." Computers in Industry 90 (2017): 42-49.
[9] Pan J, Tompkins W J. A real-time QRS detection algorithm [J]. IEEE transactions on biomedical engineering, 1985 (3): 230-236.
[10] Gradl S, Kugler P, Lohmüller C, et al. Real-time ECG monitoring and arrhythmia detection using Android-based mobile devices[C]//Engineering in Medicine and Biology Society (EMBC), 2012 Annual International Conference of the IEEE. IEEE, 2012: 2452-2455.
[11] Rizqyawan M I, Simbolon A I, Suhendra M A, et al. Mobile/android application for QRS detection using zero cross method[C]//Journal of Physics: Conference Series. IOP Publishing, 2018, 978(1): 012048.
[12] 王利琴, 顾军华, 梁志刚. 一种实时鲁棒的 QRS 波群检测算法[J]. 计算机应用与软件, 2013, 30(12): 325-328.
Real-time QRS Complexes Detection of Exercise ECG Based on Pan-Tompkins
SU Zhi-tong, WU Qiong-qiong
(Computer Institute of North China University of Technology, Beijing 100144, China)
Real-time electrocardiographic testing of people who are in motion, and timely understanding of the heart condition, can greatly reduce the number of deaths due to heart disease. The real-time detection of QRS complexes is an important research content in the exercise ECG analysis. Detecting the correct QRS complex or R-peak is an important indicator of ECG measurement. In this paper, we use the Pan-Tompkins algorithm to detect QRS complexes in exercise ECG data. The results show that this method is suitable for practical applications.
Exercise ECG; QRS complexes; Pan-Tompkins algorithm
TP391
A
10.3969/j.issn.1003-6970.2018.08.039
苏志同(1963-),男,教授,主要研究方向:计算机网络;吴琼琼(1991-),女,研究生,主要研究方向:数据挖掘。
本文著录格式:苏志同,吴琼琼. 基于Pan-Tompkins的运动心电QRS波群实时检测的研究[J]. 软件,2018,39(8):188-191

