基于Duffing系统和扩展Prony算法的异步电动机转子断条故障检测

许伯强，王志远

华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引言

异步电动机以其结构简单，制造、使用和维护方便，运行可靠，成本较低等优点，被广泛地运用到生活以及生产中。所以，异步电动机故障将会对生产产生重大影响。在异步电动机所发生的故障中，转子断条是较常出现的一种故障。发生转子断条故障的异步电动机出力下降，严重时会出现“扫膛”，损坏定子铁芯、绝缘，加剧电机损坏程度。

文献[1-3]指出，发生转子断条故障的异步电动机的定子电流中会出现特征分量——(1±2s)f1频率分量(s为转差率，f1为供电频率)。该分量常被称为边频分量，即主频分量。所以，通过分析定子电流信号、提取定子电流信号中的特征频率分量实现异步电动机转子断条故障的检测是工程上一直在使用的经典非侵入式检测方法。如文献[4-5]中所提到的异步电动机转子故障检测方法都是在频域方面提取特征故障分量，文献[6]利用Park矢量法检测异步电动机转子断条，文献[7]中引入的复杂度分析方法只是在早期故障的检测中效果较好。

本文提出利用Duffing系统在时域上对信号进行对应频率信号检测，结果直观、计算过程简单、运行时间短，在时域方面丰富了异步电动机转子故障检测的方法。由于边频分量的幅值较小，若用快速傅里叶变换FFT(Fast Fourier Transform)直接对定子电流进行频谱分析，边频分量很容易淹没在主频分量以及各种有色噪声中。本文提出的Duffing系统对所需检测的边频分量具有良好的敏感性，同时对边频分量外的噪声信号具有较强的免疫力[8-9]。当Duffing系统处于对信号频率进行高精度识别的条件下时，其对信号幅值的估算精度将会大幅度降低，然而边频分量的幅值对于转子断条故障程度的判断是至关重要的因素[10]。基于此，针对信号幅值的估算需要，提出将扩展Prony算法与Duffing系统相结合，利用扩展Prony算法求出特征分量的幅值和初相角[11-12]。

本文先以定子电流仿真信号检验所提方法的性能，取得了较理想的估算结果;然后在一台Y100L-2型3 kW笼型异步电动机上完成了相关的物理试验，试验结果表明，Duffing系统和扩展Prony算法在异步电动机转子断条故障检测中的应用是可行的。

1 Duffing系统检测特征信号原理

传统的Holmes-Duffing混沌检测模型[13]为：

x″+kx′-x+x3=Acos(ωt)

(1)

其中，k为阻尼比；-x+x3为非线性恢复力项；A为内策动力幅值；ω为内策动力频率。

式(1)对应的仿真模型为：

(2)

其中，u(t)为外界输入信号，一般u(t)=γcos(ωt)+n(t)，γ为待检测目标频率信号的幅值，n(t)为除目标频率信号以外的背景噪声。

Duffing系统检测特征信号的原理如下：将Duffing系统的内策动力幅值参数设置在混沌临界值，使Duffing系统处于混沌临界态，将时域待测信号作为Duffing系统的摄动输入Duffing系统当中。如果外部摄动信号中有与内策动力相同频率的信号，则Duffing系统由混沌临界态进入大尺度周期态。所以，将内策动力频率设置为与待检测的边频分量相同的频率，通过观察输入外部摄动信号后的Duffing系统的相图是否由混沌临界态转变为大尺度周期态来判断待检测信号中是否含有边频分量信号[14]。

2 Duffing系统的改进

经过仿真发现，传统的Holmes-Duffing系统检测模型对于低频率信号具有良好的检测性能，即当待测信号的频率ω为1 rad/s左右时检测性能最好，而对于高频率信号的检测能力较差。针对该问题，本文采用一种改进的Duffing系统[14-16]，通过广义的时间尺度变换，得到了可以检测任意频率信号的Duffing系统，具体变换过程如下。

令t=ωτ，则有：

x(t)=x(ωτ)

(3)

(4)

(5)

将上述转换代入式(2)中得：

(6)

重新建立仿真模型为：

(7)

对比式(2)、(7)可以发现，式(7)只是在原来的基础上扩大了ω倍，并没有改变Duffing系统的性质，所以传统的Holmes-Duffing系统的优良性质没有改变，同时改进后的Duffing系统可以检测任意频率的外部摄动信号，并且可以更好地区分内策动力信号与外部摄动信号，防止误判的情况发生。

3 扩展Prony算法的幅值和相角估计原理

根据Prony算法，本文提出利用复指数函数的线性组合来描述等间隔采样数据的数学模型(常称为Prony模型)，并给出了线性化的近似求解算法。通过对Prony模型进行适当扩展后对有理式功率谱密度进行估计。经典的扩展Prony算法采用的数学模型为1组p个具有任意幅值、相位、频率和衰减因子的指数函数。

令衰减因子α=0，则其离散时间的函数形式为：

(8)

在Duffing系统检测出异步电动机转子断条故障特征分量及其他分量的频率值的基础上，M和Prony极点zi就成了已知量。此时有M=2p，且zi满足式(9)。

(9)

代入p个zi的值，得到p线性方程组，通过求解可得a=(a1，a2，…，ap)。

(10)

(11)

其中，指数模型可以表示为：

(12)

通过总体最小二乘估计得：

(13)

则信号中各频率分量的相位、幅值为：

(14)

4 仿真信号分析

当异步电动机发生转子断条故障时，可以采用式(15)模拟定子电流信号。

is=A1cos(2πf1t+θ1)+A2cos[2π(1-2s)f1t+

θ2]+A3cos[2π(1+2s)f1t+θ3]+e(t)

(15)

其中，s=1.8%。取Ts=0.001 s、N=1 001、f1=50 Hz。

首先利用模拟定子电流信号检测Duffing系统和扩展Prony算法在异步电动机转子断条故障检测中应用的可行性，结果如图1和表1所示。

对比图1(c)、(d)和图1(e)、(f)可以清楚地看出，当发生转子断条故障时，相图由复杂没有规律的混沌临界态转变为了有规律的大尺度周期态，表明异步电动机的定子电流信号中存在(1+2s)f1和(1-2s)f1故障特征分量，说明异步电动机已经发生了转子断条故障。

由图1与表1可知，采样信号为短时间(1 s)内的时域信号，Duffing系统对于频率的识别是很敏感的，相图变化明显，易于判定待检测信号中是否存在异步电动机转子断条故障特征分量，然后利用扩展Prony算法精确地计算故障特征分量的幅值。将多次调整定子电流模拟信号的各个参数值进行代入验证，验证结果表明将Duffing系统和扩展Prony算法引入异步电动机转子断条故障检测是确实可行的。对于负荷波动、噪声等需要短时采样信号的情况，本文方法可取得较为理想的结果。

图1 定子电流信号和Duffing系统相图Fig.1 Stator current signals and phase diagramof Duffing system

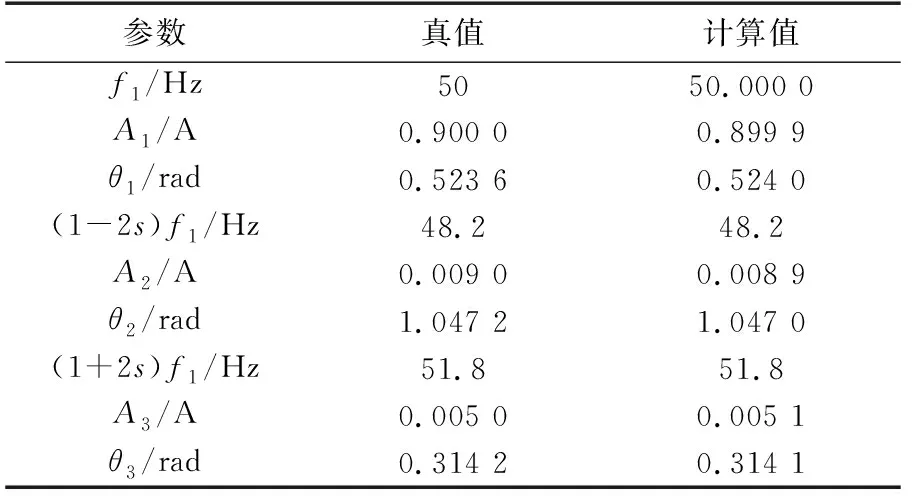
参数真值计算值f1/Hz5050.000 0A1/A0.900 00.899 9θ1/rad0.523 60.524 0(1-2s)f1/Hz48.248.2A2/A0.009 00.008 9θ2/rad1.047 21.047 0(1+2s)f1/Hz51.851.8A3/A0.005 00.005 1θ3/rad0.314 20.314 1

5 实际检测异步电动机转子断条故障

5.1 基本步骤

将Duffing系统和扩展Prony算法应用到异步电动机转子故障检测中，其基本步骤如下：

a. 采集定子电流信号is(采样频率设置为1 006 Hz，采样时长设置为10 s)；

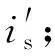
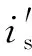
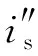
e. 根据Duffing系统的检测结果，应用扩展Prony算法估计边频分量的幅值；

f. 根据边频分量与主频分量的幅值之比以及样本参数等因素判断异步电动机是否发生了转子断条故障[10]。

5.2 实验

利用实验对本文方法和自适应滤波细化FFT法[15](下文简称FFT(10 s)法)进行对比分析。实验接线如图3所示。实验采用的三相异步电动机为Y100L-2型，额定容量为3 kW，额定电压为380 V，额定电流为6.12 A，频率为50 Hz。人为设置转子断条故障，导条断裂由钻孔形成。频谱分析在一台HP pavilion g4笔记本电脑(CPU为Intel 2.53 GHz，内存为8 GB)上进行。

图3 实验接线图Fig.3 Wiring connection of experiment

实验电动机处于半载状态时的定子a相电流、Duffing系统相图和频谱分析结果如图4所示，实验数据如表2所示，此时的转差率s=1.8%，工频分量f1=50.03 Hz。

实验电动机处于空载状态时的定子a相电流、Duffing系统相图和频谱分析结果如图5所示，实验数据如表3所示，此时的转差率s=0.3%，工频分量f1=50.03 Hz。

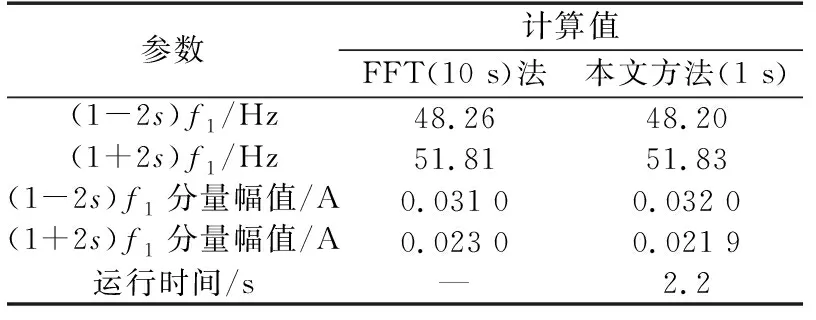
通过对比本文算法与FFT(10 s)法的实验结果与数据可知：

a. 本文方法检测特征频率的精度更高，避免了因为噪音产生误判断的情况；

b. 利用本文方法估算的特征频率分量幅值更接近真值。

图4 实验电动机半载情况下的实验结果Fig.4 Experimental results under half load condition

参数计算值FFT(10 s)法本文方法(1 s)(1-2s)f1/Hz48.2648.20(1+2s)f1/Hz51.8151.83(1-2s)f1分量幅值/A0.031 00.032 0(1+2s)f1分量幅值/A0.023 00.021 9运行时间/s—2.2

图5 实验电动机空载情况下的实验结果Fig.5 Experimental results under no load condition

参数计算值FFT(10 s)法本文方法(1 s)(1-2s)f1/Hz—49.89(1+2s)f1/Hz—50.18(1-2s)f1分量幅值/A—0.012 4(1+2s)f1分量幅值/A—0.009 8运行时间/s—2.4

综上所示，本文方法的异步电动机转子故障诊断能力优于FFT(10 s)法。

6 结论

本文将Duffing系统与扩展Prony算法结合应用于异步电动机转子断条故障检测，得出了如下结论：

a. 通过仿真模拟异步电动机转子断条故障的定子电流信号检验了本文算法的性能，结果表明，本文方法既具有Duffing系统对于噪声的免疫能力，同时又具有高频率分辨力，且可有效估计边频分量幅值；

b. 利用本文算法对1台Y100L-2型3 kW笼型异步电动机进行转子断条故障检测实验，实验结果表明，Duffing系统和扩展Prony算法可用于实际的异步电动机转子断条故障检测。

本文方法在时域上丰富了异步电动机转子断条故障检测的方法，其运算简单、结果直观的优点也为其进行在线应用奠定了相应的基础。